El intervalo de decrecimiento es un concepto fundamental en matemáticas, especialmente en el análisis de funciones. ¿Alguna vez te has preguntado cómo identificar las partes de una función que están bajando? En este artículo, vamos a desglosar este concepto de manera sencilla y accesible. Comenzaremos con la definición básica y luego exploraremos algunos ejemplos clave que te ayudarán a entenderlo mejor. Así que, si estás listo, ¡vamos a sumergirnos en el mundo del intervalo de decrecimiento!
Definición del Intervalo de Decrecimiento
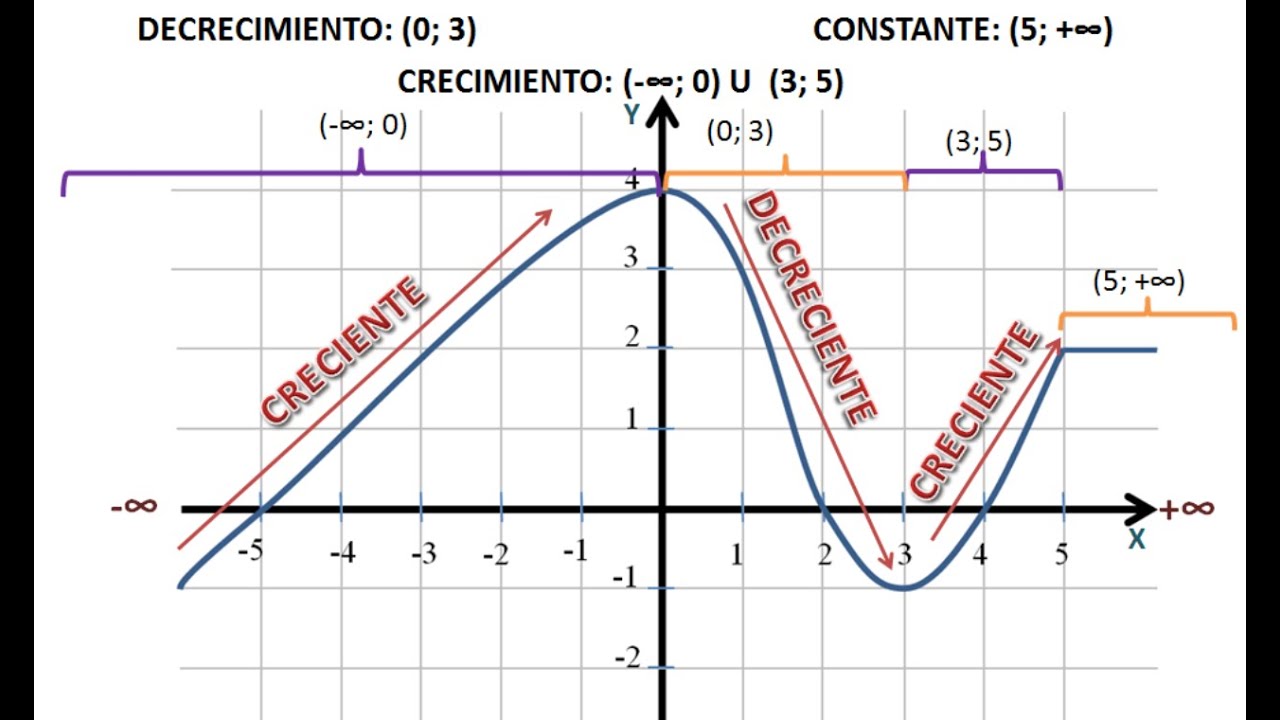
Para entender el intervalo de decrecimiento, primero necesitamos hablar sobre lo que significa «decrecer». En términos simples, una función decrece en un intervalo si, a medida que avanzamos de izquierda a derecha en ese intervalo, los valores de la función disminuyen. Es como si estuvieras bajando una colina: al principio estás en la cima, y a medida que caminas, te diriges hacia abajo. Este comportamiento se puede observar en gráficos de funciones, donde las pendientes negativas indican que la función está decreciendo.
¿Cómo Identificar un Intervalo de Decrecimiento?
Identificar un intervalo de decrecimiento implica analizar la función y su derivada. Si la derivada de una función es negativa en un intervalo dado, podemos afirmar que la función está decreciendo en ese intervalo. Por ejemplo, si tienes una función f(x) y encuentras que f'(x) < 0 para un rango de valores de x, eso significa que f(x) está decreciendo en ese rango. Es como tener un indicador que te dice si estás subiendo o bajando en una montaña. ¡Sencillo, ¿verdad?
Ejemplos Clave de Intervalos de Decrecimiento
Ahora que tenemos una idea básica de qué es el intervalo de decrecimiento, veamos algunos ejemplos concretos. Imagina que tienes la función f(x) = -x² + 4. Si graficas esta función, verás que tiene una forma de parábola que se abre hacia abajo. ¿Dónde crees que está decreciendo? Exacto, desde el vértice hacia la izquierda y hacia la derecha. En este caso, el intervalo de decrecimiento es (-∞, 0) y (0, ∞). ¿Te das cuenta de cómo una simple parábola puede mostrarte intervalos de decrecimiento?
Ejemplo 2: Función Lineal
Tomemos una función lineal como f(x) = -2x + 3. En este caso, la pendiente es negativa (-2), lo que significa que la función decrece en todo su dominio. Aquí, el intervalo de decrecimiento sería (-∞, ∞). Es interesante cómo una línea recta también puede tener intervalos de decrecimiento, ¿no crees? A veces, las cosas más simples tienen sus propias complejidades.
Propiedades del Intervalo de Decrecimiento
Al analizar intervalos de decrecimiento, hay algunas propiedades que debemos considerar. Una de ellas es que un intervalo de decrecimiento puede estar limitado o ser infinito. Por ejemplo, en el caso de la función cuadrática que mencionamos antes, los intervalos de decrecimiento son infinitos. Sin embargo, en funciones más complejas, como las racionales, podrías encontrar intervalos de decrecimiento que están limitados a un rango específico. Esto puede ser crucial al resolver problemas matemáticos más complicados.
Relación con el Intervalo de Crecimiento
Es importante mencionar que el intervalo de decrecimiento está íntimamente relacionado con el intervalo de crecimiento. Mientras que el intervalo de decrecimiento se refiere a donde la función baja, el intervalo de crecimiento se refiere a donde la función sube. A menudo, estos intervalos se encuentran separados por puntos críticos, que son los puntos donde la función cambia de comportamiento. ¿Alguna vez has jugado a los altibajos? Así es como funcionan los intervalos de crecimiento y decrecimiento en una función.
Aplicaciones Prácticas del Intervalo de Decrecimiento
El concepto de intervalo de decrecimiento no solo es relevante en el ámbito académico; también tiene aplicaciones prácticas en el mundo real. Por ejemplo, si estás analizando el rendimiento de una empresa, podrías usar funciones para modelar las ganancias a lo largo del tiempo. Identificar los intervalos de decrecimiento te permitirá ver cuándo la empresa está perdiendo dinero o cuando sus ganancias están disminuyendo. Esto puede ser invaluable para la toma de decisiones estratégicas.
Ejemplo en Economía
Imagina que estás trabajando en un proyecto para una compañía que ha visto una caída en sus ventas. Si modelas sus ventas con una función y encuentras un intervalo de decrecimiento, puedes identificar cuándo comenzó la caída y qué factores pudieron haber influido. Esto te permitirá tomar medidas para revertir la tendencia. ¡Es como tener un mapa que te muestra el camino hacia el éxito!
Desafíos al Trabajar con Intervalos de Decrecimiento
Como todo en matemáticas, trabajar con intervalos de decrecimiento puede presentar desafíos. Uno de los más comunes es confundir un intervalo de decrecimiento con una función que tiene un comportamiento oscilante. A veces, una función puede tener secciones donde decrece y luego vuelve a crecer. Es esencial prestar atención a los puntos críticos y a la derivada para no perderte en el camino. Al igual que en la vida, a veces hay que detenerse y observar para no perder la dirección.
Errores Comunes
Un error común es asumir que una función siempre decrece en un intervalo solo porque tiene una pendiente negativa en un punto. Recuerda que la derivada puede cambiar, y es fundamental analizar el comportamiento de la función en su totalidad. Es como mirar solo una parte de un rompecabezas y pensar que tienes la imagen completa. Siempre es mejor ver el panorama general.
El intervalo de decrecimiento es un concepto esencial en matemáticas que nos ayuda a comprender cómo se comportan las funciones. Desde identificar intervalos específicos hasta aplicar este conocimiento en situaciones del mundo real, la comprensión de este concepto puede ser invaluable. Así que, la próxima vez que veas una función, pregúntate: ¿dónde está decreciendo? Esa simple pregunta puede abrirte un mundo de posibilidades y comprensión.
¿El intervalo de decrecimiento siempre se encuentra entre dos puntos específicos?
No necesariamente. Puede ser un intervalo limitado o infinito. Depende de la función que estés analizando.
¿Cómo puedo encontrar los puntos críticos de una función?
Los puntos críticos se encuentran resolviendo f'(x) = 0 o donde la derivada no está definida. Estos puntos son clave para identificar intervalos de crecimiento y decrecimiento.
¿Puedo tener intervalos de decrecimiento en funciones no lineales?
¡Sí! Las funciones no lineales, como las cuadráticas o cúbicas, a menudo tienen intervalos de decrecimiento y crecimiento.
¿Qué pasa si una función no tiene intervalos de decrecimiento?
Algunas funciones pueden ser siempre crecientes o constantes. En esos casos, simplemente no tendrás intervalos de decrecimiento.
¿El intervalo de decrecimiento es lo mismo que la pendiente negativa?
No exactamente. La pendiente negativa indica que la función está decreciendo, pero el intervalo de decrecimiento se refiere a un rango específico donde esto ocurre.
Este artículo está diseñado para ser informativo y accesible, utilizando un estilo conversacional y ejemplos prácticos para facilitar la comprensión del concepto de intervalo de decrecimiento.