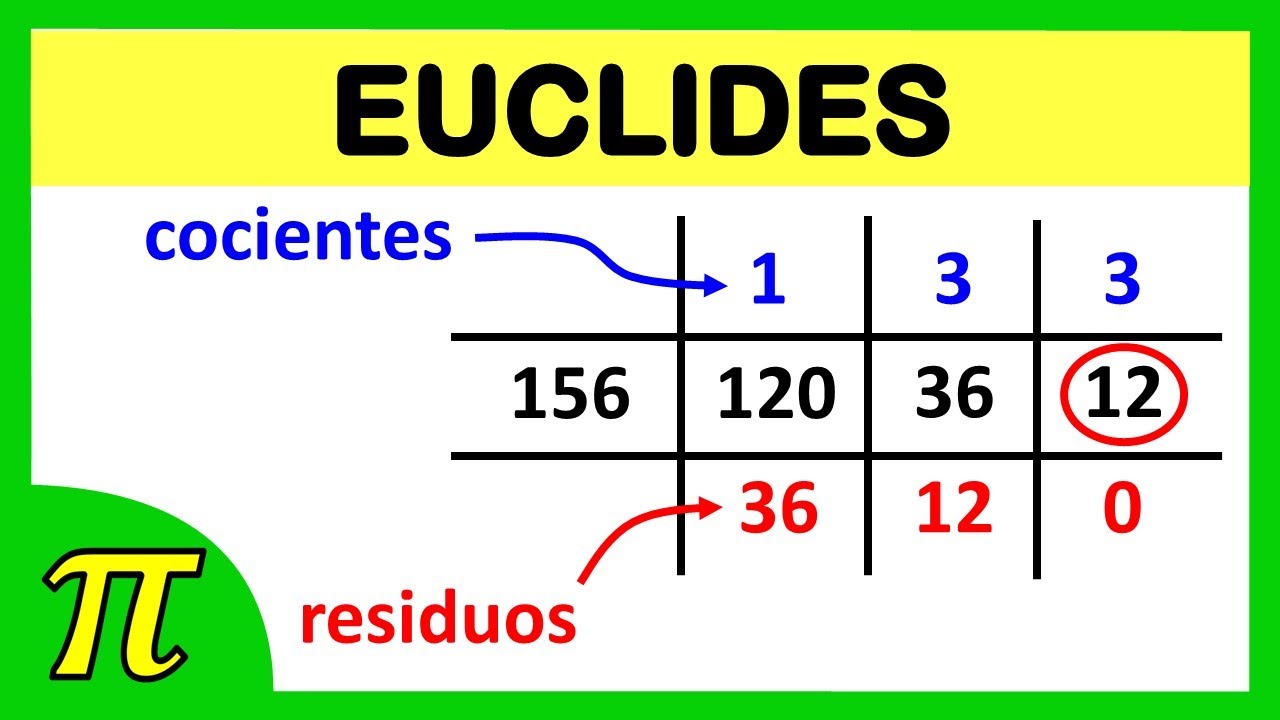
El algoritmo de Euclides es una de esas joyas matemáticas que, a pesar de su antigüedad, sigue siendo increíblemente útil hoy en día. ¿Alguna vez te has preguntado cómo se encuentran los números primos o cómo se simplifican fracciones? Este algoritmo es la respuesta. Imagínate un método tan simple que, con solo un par de pasos, puedes desentrañar el mayor común divisor (MCD) de dos números. ¿Te parece fascinante? ¡A mí también! Vamos a desglosar este tema y a sumergirnos en ejemplos prácticos que te harán sentir como un verdadero matemático.
¿Qué es el Algoritmo de Euclides?
El algoritmo de Euclides es un método que se utiliza para calcular el mayor común divisor (MCD) de dos números enteros. Fue desarrollado por el matemático griego Euclides en su obra «Los Elementos», y aunque han pasado siglos desde entonces, su eficacia no ha disminuido. En términos sencillos, el MCD de dos números es el número más grande que puede dividir ambos sin dejar un residuo. ¿Por qué es importante esto? Porque entender el MCD es esencial para simplificar fracciones y resolver problemas en teoría de números.
¿Cómo Funciona el Algoritmo?
El algoritmo es bastante sencillo. Se basa en la idea de que el MCD de dos números también es el MCD de uno de esos números y el residuo de su división. En otras palabras, si tienes dos números, digamos A y B, puedes dividir A entre B y obtener un residuo R. Luego, el MCD de A y B es el mismo que el MCD de B y R. Este proceso se repite hasta que el residuo es cero. Cuando esto sucede, el último divisor no nulo es el MCD. ¡Es como un juego de eliminación, donde solo los mejores números sobreviven!
Ejemplo Práctico 1: Encontrando el MCD de 48 y 18
Vamos a aplicar el algoritmo de Euclides con un ejemplo concreto: queremos encontrar el MCD de 48 y 18. Primero, dividimos 48 entre 18.
48 ÷ 18 = 2 (cociente) con un residuo de 12.
Ahora, aplicamos la regla: el MCD de 48 y 18 es el mismo que el MCD de 18 y 12. Ahora repetimos el proceso:
18 ÷ 12 = 1 (cociente) con un residuo de 6.
Continuamos: el MCD de 18 y 12 es el mismo que el MCD de 12 y 6.
12 ÷ 6 = 2 (cociente) con un residuo de 0.
Como el residuo es cero, el último divisor no nulo es 6. Por lo tanto, el MCD de 48 y 18 es 6. ¡Sencillo, ¿verdad?
Ejemplo Práctico 2: Encontrando el MCD de 56 y 98
Ahora, vamos a ver otro ejemplo. Supongamos que queremos encontrar el MCD de 56 y 98. Comenzamos dividiendo 98 entre 56:
98 ÷ 56 = 1 (cociente) con un residuo de 42.
Ahora, el MCD de 56 y 98 es el mismo que el MCD de 56 y 42. Continuamos:
56 ÷ 42 = 1 (cociente) con un residuo de 14.
Seguimos con el MCD de 42 y 14:
42 ÷ 14 = 3 (cociente) con un residuo de 0.
Como hemos llegado a un residuo de cero, el último divisor no nulo es 14. Por lo tanto, el MCD de 56 y 98 es 14. ¿Te sientes más cómodo con el algoritmo ahora?
Aplicaciones Prácticas del Algoritmo de Euclides
Ahora que hemos explorado cómo funciona el algoritmo, es hora de hablar de algunas aplicaciones prácticas. ¿Sabías que este algoritmo no solo se utiliza en matemáticas puras, sino que también tiene aplicaciones en la vida diaria y en áreas como la informática y la criptografía?
Simplificación de Fracciones
Una de las aplicaciones más comunes del MCD es la simplificación de fracciones. Si quieres simplificar la fracción 24/36, puedes usar el algoritmo de Euclides para encontrar el MCD, que en este caso es 12. Luego, divides tanto el numerador como el denominador por 12, resultando en la fracción simplificada 2/3. ¡Fácil y rápido!
Criptografía
En el mundo digital, la seguridad es clave. El algoritmo de Euclides se utiliza en la criptografía, específicamente en el algoritmo RSA, que protege la información en línea. Aquí, el MCD se utiliza para generar claves que aseguran que solo las personas autorizadas puedan acceder a ciertos datos. Es como tener una cerradura en tu casa que solo se abre con una llave única.
Teoría de Números
En teoría de números, el algoritmo de Euclides ayuda a resolver problemas relacionados con la divisibilidad y la factorización. Los matemáticos lo utilizan para encontrar números primos y entender mejor las propiedades de los números enteros. ¡Es una herramienta poderosa para aquellos que se sumergen en el fascinante mundo de las matemáticas!
Variaciones del Algoritmo de Euclides
Aunque el algoritmo de Euclides en su forma básica es efectivo, hay variaciones que pueden ser útiles en diferentes contextos. Una de ellas es el Algoritmo de Euclides Extendido, que no solo encuentra el MCD de dos números, sino que también proporciona coeficientes que pueden expresar el MCD como una combinación lineal de esos números. Esto es especialmente útil en problemas de teoría de números y en la resolución de ecuaciones diofantinas.
¿Cómo Funciona el Algoritmo de Euclides Extendido?
El algoritmo de Euclides extendido sigue el mismo principio que el algoritmo original, pero además, mantiene un seguimiento de los coeficientes de cada paso. Si tomamos los números A y B, y aplicamos el algoritmo, podemos expresar el MCD como:
MCD(A, B) = Ax + By, donde x y y son los coeficientes que encontramos a lo largo del proceso. Este enfoque proporciona una solución más rica y detallada que puede ser aplicada en diversos problemas matemáticos.
El algoritmo de Euclides es un ejemplo perfecto de cómo un concepto matemático simple puede tener un impacto profundo en una variedad de campos. Desde la simplificación de fracciones hasta la seguridad digital, su utilidad es innegable. Ahora que tienes una comprensión clara de cómo funciona, así como algunos ejemplos prácticos, ¿te sientes listo para aplicar este conocimiento en tu vida diaria? La próxima vez que necesites simplificar una fracción o resolver un problema de divisibilidad, recuerda que el algoritmo de Euclides está a tu disposición.
¿El algoritmo de Euclides solo funciona con números enteros?
Sí, el algoritmo de Euclides está diseñado para trabajar con números enteros. No se puede aplicar directamente a números decimales o fracciones.
¿Puedo usar el algoritmo de Euclides para encontrar el MCD de más de dos números?
¡Claro! Puedes encontrar el MCD de más de dos números aplicando el algoritmo de forma secuencial. Por ejemplo, para tres números A, B y C, primero encontrarías el MCD de A y B, y luego usarías ese resultado para encontrar el MCD con C.
¿El algoritmo de Euclides es eficiente?
Sí, es muy eficiente, especialmente en comparación con otros métodos para encontrar el MCD. Su tiempo de ejecución es logarítmico en relación con el tamaño de los números, lo que significa que incluso para números grandes, el algoritmo funciona rápidamente.
¿Cómo puedo practicar el algoritmo de Euclides?
Una buena manera de practicar es elegir pares de números enteros y aplicar el algoritmo paso a paso. Puedes usar calculadoras en línea para verificar tus resultados o incluso crear tus propios ejercicios para resolver.