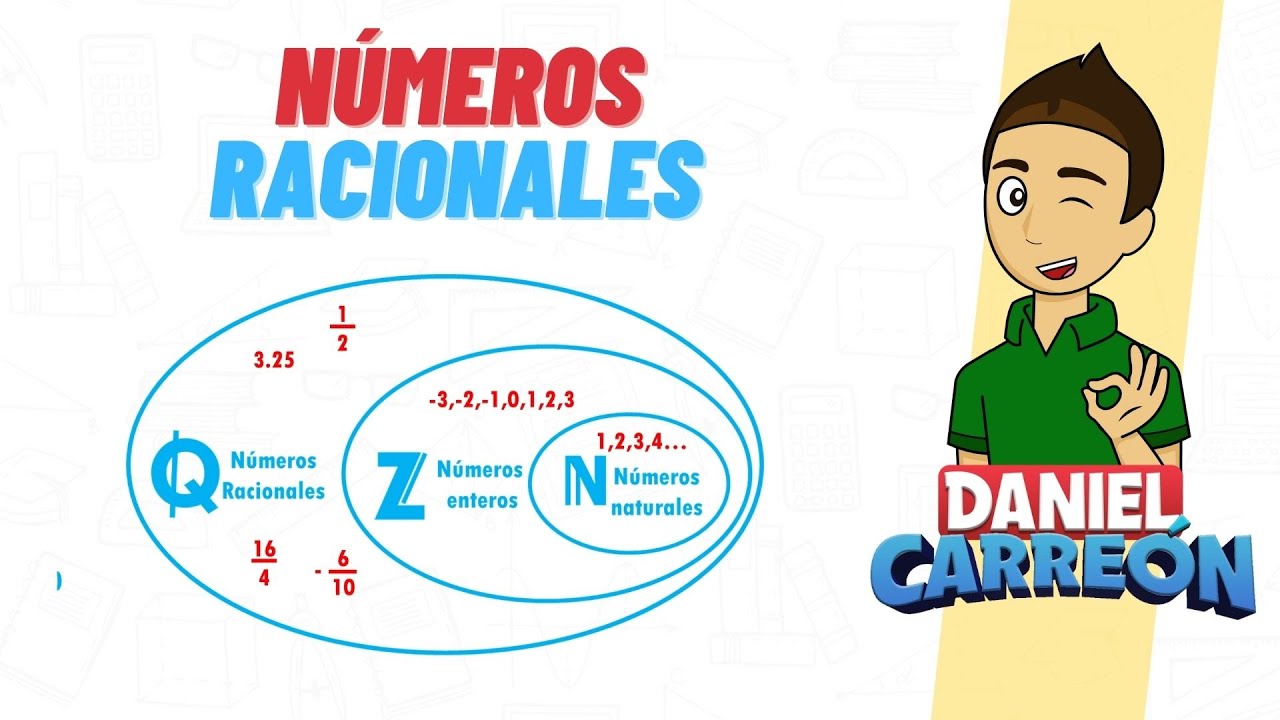
Los números racionales son una parte fundamental de las matemáticas que muchas veces nos encontramos en nuestro día a día, aunque no siempre nos damos cuenta. ¿Recuerdas esa vez que dividiste una pizza entre amigos? Cada porción que recibieron es un ejemplo de un número racional. En términos matemáticos, un número racional es cualquier número que se puede expresar como el cociente de dos enteros, donde el denominador no puede ser cero. Esto significa que puedes tener fracciones como 1/2, 3/4, o incluso números enteros como 5 (que se puede escribir como 5/1). Ahora bien, ¿por qué es importante comprender los números racionales? Porque dominarlos te permite resolver problemas más complejos y aplicarlos en situaciones cotidianas.
En este artículo, te llevaré de la mano a través de ejercicios prácticos que te ayudarán a mejorar tu comprensión de los números racionales. Desde operaciones básicas hasta aplicaciones en problemas del mundo real, aquí encontrarás todo lo que necesitas para convertirte en un maestro de los números racionales. Así que, ¿estás listo para sumergirte en el fascinante mundo de las fracciones y los decimales? ¡Vamos a ello!
¿Qué son los Números Racionales?
Los números racionales son aquellos que se pueden expresar en forma de fracción. Esto incluye tanto números positivos como negativos, e incluso el cero. Si piensas en ellos como partes de un todo, te darás cuenta de que son increíblemente versátiles. Por ejemplo, si tienes una torta y decides compartirla entre cuatro amigos, cada uno recibirá 1/4 de la torta. Aquí, 1 es el numerador (la parte que tienes) y 4 es el denominador (el total de partes). Pero no se detiene ahí; los números racionales también se pueden representar como decimales. Por ejemplo, 1/2 es igual a 0.5. Así que, si alguna vez has tenido que lidiar con porcentajes, fracciones o cualquier tipo de división, has estado trabajando con números racionales sin siquiera darte cuenta.
Operaciones Básicas con Números Racionales
Suma y Resta de Fracciones
Comencemos con las operaciones más simples: la suma y la resta. Imagina que tienes dos fracciones, 1/4 y 1/2. Para sumarlas, necesitas un denominador común. En este caso, el denominador común sería 4. Así que convertirías 1/2 a 2/4. Ahora, suma: 1/4 + 2/4 = 3/4. ¡Así de fácil!
¿Y si quisiéramos restar? Digamos que tienes 3/4 y quieres restar 1/4. Simplemente haces 3/4 – 1/4 = 2/4, que se puede simplificar a 1/2. Recuerda que la clave está en encontrar un denominador común y luego realizar la operación. Esto te ayudará a evitar confusiones y a realizar cálculos más fácilmente.
Multiplicación de Fracciones
La multiplicación de fracciones es aún más sencilla. Para multiplicar 1/2 por 3/4, simplemente multiplicas los numeradores y los denominadores: (1 * 3) / (2 * 4) = 3/8. ¡Voilà! No necesitas un denominador común, lo que hace que esta operación sea rápida y eficiente. Ahora, si quieres multiplicar fracciones con números enteros, simplemente convierte el entero a fracción. Por ejemplo, 5 puede ser 5/1, así que 5/1 * 1/2 = 5/2.
División de Fracciones
La división puede sonar complicada, pero en realidad es bastante simple. Para dividir una fracción, multiplicas por el recíproco de la otra. Por ejemplo, si quieres dividir 1/2 entre 1/4, multiplicas 1/2 por 4/1, lo que te da 4/2, que se simplifica a 2. Así que, cuando se trata de números racionales, ¡no hay que temer a la división!
Ejercicios Prácticos para Mejorar tu Comprensión
Ahora que hemos cubierto las operaciones básicas, es hora de poner a prueba tus habilidades con algunos ejercicios prácticos. Te invito a que tomes papel y lápiz, o tu dispositivo preferido, y te sumerjas en estos problemas. Recuerda, la práctica hace al maestro.
Ejercicio 1: Suma de Fracciones
Calcula la siguiente suma: 2/3 + 1/6. ¿Cuál es el resultado? Tómate tu tiempo para encontrar un denominador común y resolverlo.
Ejercicio 2: Resta de Fracciones
Ahora intenta restar: 5/6 – 1/2. ¿Puedes simplificar la respuesta?
Ejercicio 3: Multiplicación de Fracciones
Multiplica las siguientes fracciones: 3/5 * 2/3. ¿Qué obtienes?
Ejercicio 4: División de Fracciones
Finalmente, divide 1/2 entre 2/5. ¿Cuál es el resultado?
Recuerda que la práctica constante te ayudará a dominar estos conceptos y a sentirte más cómodo al trabajar con números racionales.
Aplicaciones de los Números Racionales en la Vida Real
Ahora que has practicado algunas operaciones básicas, es hora de explorar cómo se aplican los números racionales en la vida cotidiana. Desde las compras hasta la cocina, estos números están en todas partes.
Cocina y Recetas
Imagina que estás cocinando y necesitas ajustar una receta. Si la receta original requiere 3/4 de taza de azúcar, pero solo quieres hacer la mitad de la receta, necesitarás calcular cuánto es 3/4 dividido por 2. Esto te da 3/8 de taza. Sin duda, los números racionales te permiten ajustar las cantidades de manera precisa y efectiva.
Finanzas Personales
Los números racionales también juegan un papel crucial en las finanzas. Supón que tienes una deuda de $1,000 y decides pagar 1/4 de ella cada mes. Cada mes estarías pagando $250. Esto te ayuda a gestionar tus finanzas y a planificar tus pagos de manera efectiva.
Construcción y Medidas
En el ámbito de la construcción, las fracciones son esenciales para medir y cortar materiales. Si un tablón de madera mide 2 1/2 pies y necesitas cortarlo en tres partes iguales, tendrás que calcular 2 1/2 dividido por 3, lo que te dará 5/6 de pie por parte. Este tipo de cálculo es esencial para garantizar que los proyectos se realicen de manera precisa.
Errores Comunes al Trabajar con Números Racionales
Es natural cometer errores, especialmente cuando se trata de fracciones. Aquí hay algunos errores comunes que debes evitar:
Confundir el Numerador y el Denominador
Es fácil confundirse y mezclar el numerador con el denominador. Recuerda que el numerador es la parte de arriba y el denominador es la parte de abajo. Si alguna vez te encuentras en duda, revisa tu trabajo y asegúrate de que los números están en su lugar correcto.
No Encontrar un Denominador Común
Cuando sumas o restas fracciones, olvidarse de encontrar un denominador común puede llevar a errores. Asegúrate de siempre buscar el denominador que comparten ambas fracciones antes de realizar la operación.
Olvidar Simplificar
Después de realizar operaciones, a menudo olvidamos simplificar la respuesta. Siempre verifica si tu respuesta se puede reducir a una forma más simple. Esto no solo te ayudará a obtener la respuesta correcta, sino que también te facilitará el trabajo con números en el futuro.
En resumen, los números racionales son una parte esencial de las matemáticas que tienen aplicaciones en la vida diaria. A través de la práctica constante y la comprensión de las operaciones básicas, puedes dominar este concepto y utilizarlo en diversas situaciones. Recuerda que la clave está en practicar y no tener miedo de cometer errores; son parte del proceso de aprendizaje. Así que, ¿qué esperas? ¡Sigue practicando y mejora tu comprensión de los números racionales!
¿Qué son los números racionales?
Los números racionales son aquellos que se pueden expresar como el cociente de dos enteros, donde el denominador no puede ser cero. Esto incluye fracciones, números enteros y decimales finitos.
¿Cómo puedo practicar los números racionales?
Puedes practicar los números racionales resolviendo ejercicios de suma, resta, multiplicación y división de fracciones. También puedes aplicarlos en situaciones cotidianas como cocinar o manejar tus finanzas.
¿Por qué son importantes los números racionales?
Los números racionales son importantes porque son fundamentales para comprender conceptos más complejos en matemáticas y se aplican en diversas áreas de la vida diaria, como la cocina, las finanzas y la construcción.
¿Cuál es la diferencia entre un número racional y un número irracional?
Los números racionales pueden expresarse como una fracción de dos enteros, mientras que los números irracionales no pueden representarse de esa manera. Ejemplos de números irracionales son √2 y π.