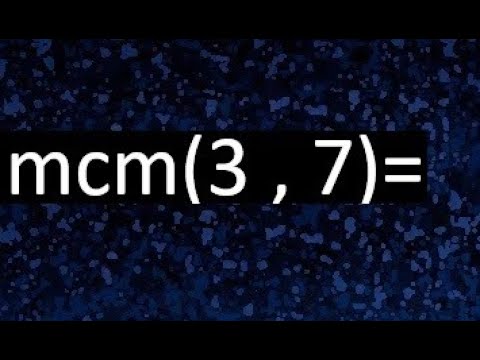Entendiendo el Mínimo Común Múltiplo
¡Hola, amigo lector! Hoy vamos a sumergirnos en el fascinante mundo de los números y aprender cómo calcular el Mínimo Común Múltiplo (MCM) de dos números, en este caso, 3 y 7. Pero antes de entrar en materia, ¿qué es exactamente el MCM? Piensa en el MCM como el «punto de encuentro» más pequeño donde se cruzan dos trenes que viajan a diferentes velocidades. En nuestro caso, esos trenes son 3 y 7, y estamos buscando el primer momento en que ambos trenes llegan a la misma estación. Suena interesante, ¿verdad? Vamos a hacerlo paso a paso.
¿Qué es el Mínimo Común Múltiplo?
Para que no te pierdas en el camino, empecemos con una breve definición. El Mínimo Común Múltiplo de dos o más números es el número más pequeño que es múltiplo de cada uno de esos números. Por ejemplo, los múltiplos de 3 son 3, 6, 9, 12, 15, 18, etc. Y los múltiplos de 7 son 7, 14, 21, 28, 35, etc. Entonces, ¿cuál es el primer número que aparece en ambas listas? ¡Exacto! Es 21. Pero no te preocupes si no lo viste de inmediato; aquí te guiaré para que puedas hacerlo tú mismo, y no solo con 3 y 7, sino con cualquier par de números que desees.
Método 1: Listar Múltiplos
Paso 1: Identificar los Múltiplos
El primer método, y quizás el más sencillo, consiste en listar los múltiplos de cada número. Empezamos con 3. Vamos a escribir algunos múltiplos de 3:
- 3
- 6
- 9
- 12
- 15
- 18
- 21
- 24
- 27
- 30
Ahora, hagamos lo mismo con 7:
- 7
- 14
- 21
- 28
- 35
Paso 2: Buscar el Mínimo Común Múltiplo
Una vez que tenemos nuestras listas, simplemente buscamos el número más pequeño que aparece en ambas. ¿Cuál es? ¡Correcto! Es 21. Así que, el MCM de 3 y 7 es 21. Este método es fácil y directo, pero puede volverse tedioso si trabajamos con números más grandes. ¿Te imaginas listar los múltiplos de 100? Definitivamente necesitarías un café extra para eso.
Método 2: Factorización Prima
Paso 1: Descomponer los Números
Ahora, vamos a probar un enfoque diferente: la factorización prima. Este método es un poco más técnico, pero no te preocupes, lo desglosaremos. Primero, necesitamos descomponer 3 y 7 en sus factores primos. En este caso, ambos son números primos, así que su factorización es bastante simple:
- 3 = 3
- 7 = 7
Paso 2: Tomar los Factores Más Altos
El siguiente paso es tomar todos los factores primos que hemos encontrado, y elegir el más alto de cada uno. Como tenemos 3 y 7, simplemente los multiplicamos:
3 x 7 = 21
Y ahí lo tienes, el MCM de 3 y 7 es 21. Este método es muy útil, especialmente cuando trabajamos con números más grandes, ya que no tenemos que lidiar con listas interminables de múltiplos.
Método 3: Usar la Relación con el Máximo Común Divisor
Paso 1: Calcular el Máximo Común Divisor
¿Sabías que hay una relación entre el MCM y el Máximo Común Divisor (MCD)? La fórmula es: MCM(a, b) = (a * b) / MCD(a, b). Así que, para calcular el MCM de 3 y 7, primero necesitamos encontrar su MCD. Como 3 y 7 no tienen factores en común, su MCD es 1.
Paso 2: Aplicar la Fórmula
Ahora que sabemos que el MCD es 1, podemos aplicar la fórmula:
MCM(3, 7) = (3 * 7) / 1 = 21
Este método es bastante elegante y te permite conectar conceptos matemáticos. Es como descubrir que dos amigos tienen un conocido en común, ¡y ahora puedes hacer una fiesta juntos!
Aplicaciones del Mínimo Común Múltiplo
Ahora que sabemos cómo calcular el MCM, ¿por qué es tan importante? Bueno, el MCM tiene muchas aplicaciones prácticas. Por ejemplo, es fundamental en la resolución de problemas de fracciones, donde necesitas encontrar un denominador común. Imagina que estás cocinando y necesitas ajustar recetas; saber el MCM puede ayudarte a mezclar ingredientes de manera precisa. También es útil en la programación y en la teoría de números, donde la eficiencia en los cálculos es clave.
Errores Comunes al Calcular el MCM
Aunque calcular el MCM no es complicado, hay algunos errores comunes que la gente suele cometer. Uno de ellos es confundir el MCM con el MCD. Recuerda, el MCD es el número más grande que divide a ambos números, mientras que el MCM es el más pequeño que ambos pueden dividir. Otro error es no listar todos los múltiplos o no tener en cuenta los factores primos. Si te encuentras atascado, ¡no dudes en revisar tus pasos!
Práctica: Ejercicios para Ti
Ahora que has aprendido cómo calcular el MCM de 3 y 7, ¡es tu turno! Intenta calcular el MCM de los siguientes pares de números:
- 4 y 5
- 6 y 8
- 9 y 12
- 10 y 15
Recuerda, puedes usar cualquiera de los métodos que hemos discutido. Una vez que termines, verifica tus respuestas con un amigo o busca en línea. ¡La práctica hace al maestro!
Calcular el Mínimo Común Múltiplo de dos números como 3 y 7 puede parecer complicado al principio, pero como has visto, hay varios métodos para hacerlo. Ya sea que prefieras listar múltiplos, usar la factorización prima o aplicar la relación con el MCD, lo importante es entender el concepto detrás de ello. Así que la próxima vez que necesites encontrar el MCM, estarás listo para hacerlo con confianza.
¿Puedo calcular el MCM de más de dos números?
¡Claro que sí! Simplemente aplica cualquiera de los métodos que hemos discutido, tomando cada par de números uno a uno hasta que hayas encontrado el MCM de todos ellos.
¿El MCM siempre será mayor que ambos números?
No necesariamente. En algunos casos, como con números idénticos, el MCM será igual a ese número. Por ejemplo, el MCM de 5 y 5 es 5.
¿El MCM puede ser un número negativo?
No, el MCM siempre es un número positivo, ya que estamos hablando de múltiplos. Los múltiplos de un número siempre son positivos.
¿Cómo puedo aplicar el MCM en la vida real?
El MCM es útil en situaciones como la programación de eventos, la resolución de problemas de fracciones y la optimización de recursos en proyectos. ¡Es una herramienta valiosa en muchas áreas!
¿Qué debo hacer si tengo números muy grandes?
Para números grandes, la factorización prima o el uso del MCD son los métodos más eficientes. No dudes en usar calculadoras o software matemático si es necesario.