¿Qué son los Vectores Equipolentes?
¡Hola, amigo lector! Hoy vamos a sumergirnos en el fascinante mundo de los vectores equipolentes. Pero antes de que te sientas abrumado por la terminología técnica, permíteme desglosar esto de una manera sencilla. Imagina que estás en un parque y tienes dos amigos que te empujan en direcciones diferentes. Aunque las fuerzas que aplican son distintas, si la suma de sus empujones resulta en un efecto similar al de un solo empujón, podríamos decir que sus fuerzas son equipolentes. En términos más técnicos, los vectores equipolentes son aquellos que tienen la misma magnitud y dirección, aunque puedan estar aplicándose en diferentes puntos del espacio.
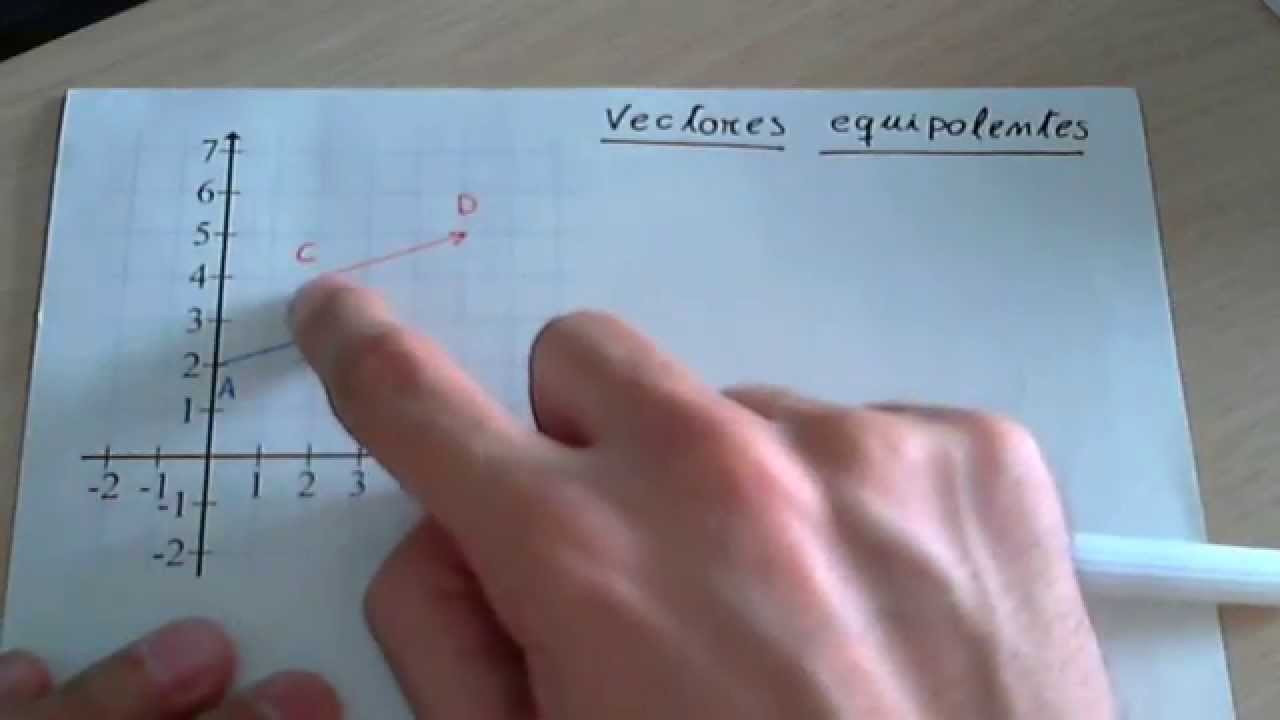
Definición y Propiedades de los Vectores Equipolentes
Los vectores equipolentes se definen como aquellos vectores que tienen la misma magnitud y dirección, pero pueden tener diferentes puntos de aplicación. ¿Te suena complicado? Piensa en un carro que se mueve hacia adelante. Si aplicas una fuerza en la parte delantera y otra en la trasera, pero ambas tienen la misma intensidad y dirección, el carro se moverá igual que si solo se hubiera aplicado una única fuerza en el centro. En términos matemáticos, dos vectores A y B son equipolentes si A = B. Es decir, no importa dónde se apliquen, el resultado final es el mismo.
Ejemplos de Vectores Equipolentes en la Vida Cotidiana
Para que te quede más claro, vamos a ver algunos ejemplos de vectores equipolentes en situaciones cotidianas. Imagina que estás empujando un carrito de supermercado. Si empujas desde el frente con una fuerza de 10 N hacia adelante, y tu amigo empuja desde la parte trasera con la misma fuerza y dirección, el carrito se moverá hacia adelante como si solo hubiera una fuerza. Aquí, ambas fuerzas son equipolentes.
Ejemplo 1: Fuerzas en un Juego de Tira y Afloja
Pensando en un juego de tira y afloja, donde dos equipos tiran de una cuerda en direcciones opuestas. Si ambos equipos aplican la misma fuerza, digamos 100 N, la cuerda no se moverá. En este caso, las fuerzas son equipolentes porque se cancelan entre sí. Si uno de los equipos decide aumentar su fuerza a 120 N, el otro equipo deberá aumentar su fuerza también si quiere mantener el equilibrio. Este equilibrio de fuerzas es un claro ejemplo de vectores equipolentes en acción.
Ejemplo 2: Efecto de las Corrientes de Agua
Imagina que estás en un río. Si dos corrientes de agua se encuentran, pero tienen la misma fuerza y dirección, se sumarán y el efecto será como si una sola corriente estuviera fluyendo con más fuerza. Aquí, las corrientes son vectores equipolentes, ya que su magnitud y dirección son las mismas, lo que resulta en un solo flujo más potente.
Aplicaciones de los Vectores Equipolentes
Los vectores equipolentes tienen múltiples aplicaciones en la física y la ingeniería. Por ejemplo, en la construcción, los ingenieros deben asegurarse de que las fuerzas aplicadas a una estructura se equilibran adecuadamente. Si se aplican fuerzas equipolentes, la estructura se mantendrá estable. Además, en la mecánica, el análisis de fuerzas equipolentes es crucial para entender el movimiento de los cuerpos. Si un objeto tiene múltiples fuerzas actuando sobre él, pero estas son equipolentes, el objeto no se moverá, lo que permite predecir su comportamiento.
Ejemplo en la Ingeniería
En ingeniería civil, cuando se diseñan puentes, se deben considerar las fuerzas de compresión y tensión. Si un puente está sometido a fuerzas equipolentes, los ingenieros deben asegurarse de que la estructura sea capaz de soportar estas fuerzas sin colapsar. Aquí, el concepto de vectores equipolentes se vuelve fundamental para garantizar la seguridad y la estabilidad de la construcción.
Ejemplo en la Mecánica
En la mecánica, cuando un objeto está en equilibrio, se dice que las fuerzas que actúan sobre él son equipolentes. Por ejemplo, si tienes un objeto en una balanza, las fuerzas de gravedad que actúan hacia abajo deben ser equilibradas por las fuerzas de reacción hacia arriba. Si estas fuerzas son equipolentes, el objeto permanecerá en reposo. Esto es crucial para entender cómo funcionan los sistemas mecánicos y para diseñar máquinas eficientes.
Relación entre Vectores Equipolentes y el Principio de Superposición
El principio de superposición es un concepto que complementa el estudio de los vectores equipolentes. Este principio establece que, cuando múltiples fuerzas actúan sobre un objeto, el efecto total es la suma vectorial de todas las fuerzas individuales. Esto significa que, si tienes varias fuerzas actuando sobre un objeto, puedes analizar cada una de ellas por separado y luego sumarlas para obtener el efecto total. Si el resultado es un vector equipolente, el objeto no se moverá.
Ejemplo de Superposición en un Sistema de Fuerzas
Imagina que tienes un objeto que está siendo empujado por tres fuerzas diferentes: 5 N hacia la derecha, 3 N hacia la izquierda y 2 N hacia arriba. Si sumas estas fuerzas, verás que el resultado no es cero, lo que significa que el objeto se moverá. Sin embargo, si tuvieras fuerzas equipolentes que se cancelan, como 5 N hacia la derecha y 5 N hacia la izquierda, el objeto permanecería en reposo. Este es un claro ejemplo de cómo funciona el principio de superposición en conjunto con los vectores equipolentes.
Desafíos Comunes al Trabajar con Vectores Equipolentes
Trabajar con vectores equipolentes puede parecer fácil, pero hay algunos desafíos comunes que los estudiantes y profesionales enfrentan. Uno de ellos es la representación gráfica. A veces, visualizar vectores en un diagrama puede ser complicado, especialmente cuando se trata de fuerzas en diferentes direcciones. Es crucial practicar la representación gráfica para poder identificar fácilmente los vectores equipolentes en un sistema de fuerzas.
Errores Comunes en la Identificación de Vectores Equipolentes
Otro error común es confundir magnitud y dirección. Asegúrate de que, al comparar dos vectores, realmente tengan la misma magnitud y dirección. Puede que parezcan similares, pero si una fuerza es más fuerte o apunta en una dirección diferente, no serán equipolentes. También es importante tener en cuenta el punto de aplicación de las fuerzas, ya que dos vectores pueden ser equipolentes en magnitud y dirección, pero si se aplican en puntos diferentes, su efecto podría no ser el mismo.
En resumen, los vectores equipolentes son un concepto fundamental en la física y la ingeniería que nos ayuda a entender cómo las fuerzas interactúan entre sí. Ya sea que estés empujando un carrito de supermercado, jugando a tira y afloja o diseñando un puente, reconocer y aplicar el concepto de vectores equipolentes es esencial. Así que, la próxima vez que te encuentres en una situación en la que las fuerzas parecen estar en equilibrio, recuerda: ¡puede que estés tratando con vectores equipolentes!
- ¿Todos los vectores equipolentes son necesariamente iguales? No, los vectores equipolentes tienen la misma magnitud y dirección, pero pueden aplicarse en diferentes puntos del espacio.
- ¿Cómo puedo identificar vectores equipolentes en un problema? Debes asegurarte de comparar la magnitud y la dirección de los vectores. Si son iguales, son equipolentes.
- ¿Por qué son importantes los vectores equipolentes en la ingeniería? Son cruciales para garantizar la estabilidad y seguridad de estructuras, ya que permiten entender cómo las fuerzas se equilibran en un sistema.
- ¿Pueden existir vectores equipolentes en diferentes planos? Sí, siempre y cuando tengan la misma magnitud y dirección, pueden estar en diferentes planos.
Este artículo está diseñado para ser accesible y comprensible, mientras se exploran los vectores equipolentes de una manera que involucra al lector y le proporciona ejemplos y explicaciones claras.