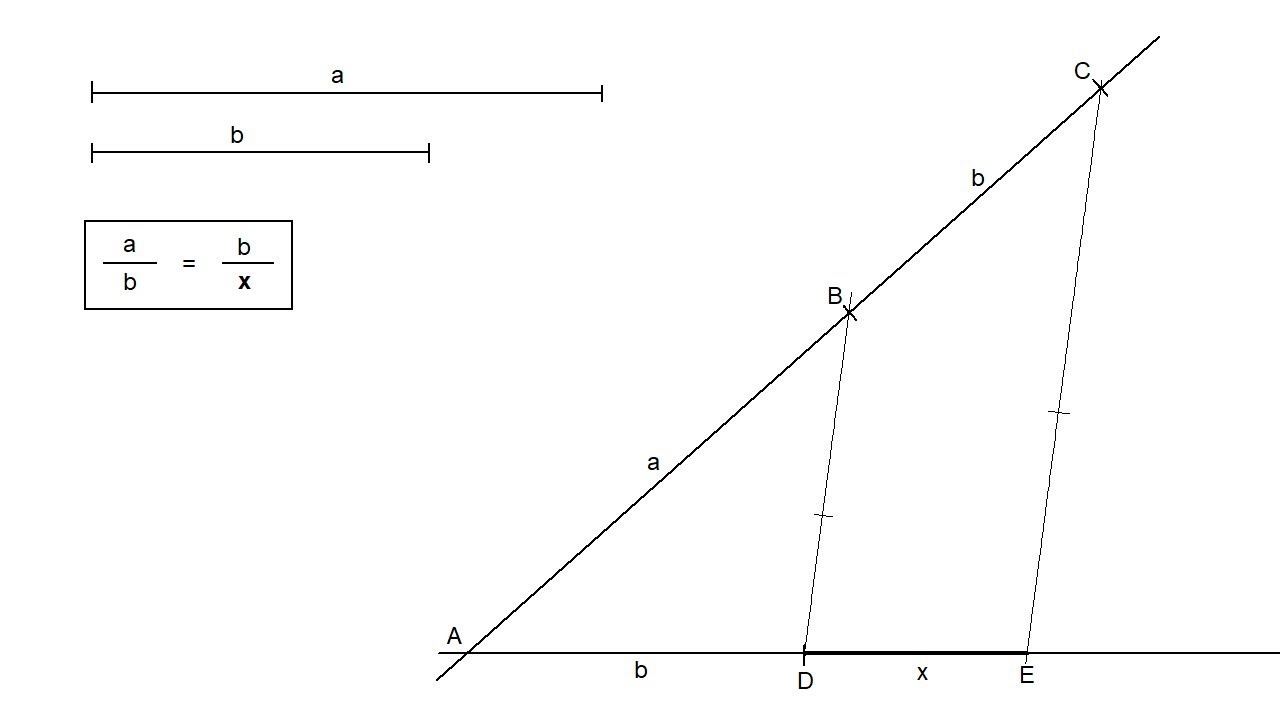
Entendiendo el Concepto del Tercero Proporcional
¿Alguna vez te has encontrado en una situación donde necesitas calcular una relación entre tres cantidades? Si es así, ¡estás en el lugar correcto! Hoy vamos a desglosar cómo calcular el tercero proporcional de manera sencilla y con ejemplos prácticos que te ayudarán a entender este concepto matemático. El tercero proporcional es un término que se utiliza a menudo en matemáticas, especialmente en la geometría y en situaciones de proporciones. En este artículo, te guiaré paso a paso a través del proceso, asegurándome de que comprendas cada parte. Así que, ¡prepárate para sumergirte en el mundo de las proporciones!
¿Qué es el Tercero Proporcional?
Primero, definamos qué es exactamente el tercero proporcional. Imagina que tienes dos cantidades, digamos A y B. El tercero proporcional es un número C que se relaciona con A y B de tal manera que la proporción entre A y B es la misma que la proporción entre B y C. En términos más simples, si A es a B como B es a C, entonces C es el tercero proporcional. Este concepto puede parecer un poco abstracto, pero lo verás más claro con un ejemplo.
Ejemplo Básico de Tercero Proporcional
Supongamos que tenemos las cantidades 2 y 3. Queremos encontrar el tercero proporcional. Usando la relación que mencionamos, podemos establecer la siguiente proporción:
2 : 3 = 3 : C
Ahora, si multiplicamos en cruz (una técnica que facilita el cálculo de proporciones), obtenemos:
2 * C = 3 * 3
Esto se traduce en:
2C = 9
Para encontrar C, simplemente dividimos ambos lados de la ecuación entre 2:
C = 9/2 = 4.5
Así que, en este caso, el tercero proporcional de 2 y 3 es 4.5. ¡Sencillo, verdad?
¿Por Qué es Útil el Tercero Proporcional?
Ahora que sabemos qué es el tercero proporcional, te estarás preguntando: «¿Para qué me sirve esto en la vida real?» Bueno, hay muchas aplicaciones prácticas. Por ejemplo, en la arquitectura, los diseñadores a menudo utilizan proporciones para crear estructuras visualmente atractivas. Además, en la economía, el tercero proporcional puede ayudar a entender relaciones entre precios, costos y ganancias. Así que, aunque parezca un concepto matemático, su aplicación es bastante amplia.
Relaciones en la Vida Cotidiana
Imagina que estás cocinando y necesitas ajustar una receta. Si la receta original es para 4 personas y tú quieres hacerla para 6, el tercero proporcional te ayudará a calcular la cantidad de cada ingrediente que necesitas. Si la receta requiere 2 tazas de harina para 4 personas, ¿cuánto necesitarás para 6? Usando el tercero proporcional, puedes establecer una relación y calcularlo fácilmente.
Cálculo del Tercero Proporcional: Un Método Paso a Paso
Ahora que hemos cubierto la teoría y algunas aplicaciones, vamos a entrar en el proceso de cálculo del tercero proporcional. Aquí tienes un método paso a paso que puedes seguir:
Paso 1: Identificar las Cantidades
Primero, debes identificar las dos cantidades entre las que deseas encontrar el tercero proporcional. Asegúrate de que estén en la misma unidad de medida para evitar confusiones. Por ejemplo, si tienes 5 y 10, ambas deben ser en la misma unidad, digamos en kilogramos.
Paso 2: Establecer la Proporción
Como mencionamos anteriormente, establece la proporción. Si A es 5 y B es 10, la relación se vería así:
5 : 10 = 10 : C
Paso 3: Multiplicar en Cruz
Ahora, multiplica en cruz:
5 * C = 10 * 10
Esto te dará:
5C = 100
Paso 4: Despejar C
Finalmente, despeja C dividiendo ambos lados de la ecuación entre 5:
C = 100 / 5 = 20
Así que, en este caso, el tercero proporcional de 5 y 10 es 20. ¡Fácil, verdad?
Ejemplos Prácticos Adicionales
Para asegurarnos de que has comprendido bien, aquí te dejo algunos ejemplos adicionales. Recuerda seguir el mismo proceso que hemos discutido.
Ejemplo 1
Digamos que tienes las cantidades 4 y 8. Queremos encontrar el tercero proporcional:
4 : 8 = 8 : C
Multiplicamos en cruz:
4C = 8 * 8
4C = 64
Despejamos C:
C = 64 / 4 = 16
Entonces, el tercero proporcional de 4 y 8 es 16.
Ejemplo 2
Ahora, probemos con 6 y 9:
6 : 9 = 9 : C
Multiplicamos en cruz:
6C = 9 * 9
6C = 81
Despejamos C:
C = 81 / 6 = 13.5
Así que el tercero proporcional de 6 y 9 es 13.5.
Consejos para Evitar Errores Comunes
Calcular el tercero proporcional puede parecer sencillo, pero hay algunos errores comunes que debes evitar. Aquí te dejo algunos consejos:
- Verifica las Unidades: Siempre asegúrate de que las cantidades estén en las mismas unidades antes de realizar cualquier cálculo.
- Multiplicación y División: Asegúrate de realizar correctamente las multiplicaciones y divisiones. Un error en este paso puede llevar a resultados incorrectos.
- Revisa tu Proporción: Antes de despejar C, verifica que hayas establecido correctamente la proporción. Un pequeño error aquí puede cambiar todo el resultado.
¿El tercero proporcional se aplica solo a números enteros?
No, el tercero proporcional se puede calcular con cualquier tipo de número, ya sean enteros, fracciones o decimales. La clave es mantener la relación proporcional.
¿Puedo usar el tercero proporcional en geometría?
¡Definitivamente! En geometría, el tercero proporcional se utiliza a menudo para resolver problemas relacionados con triángulos y figuras similares.
¿Existen otras formas de calcular el tercero proporcional?
Sí, aunque el método de multiplicación en cruz es el más común, también puedes usar el método de la regla de tres, que es muy útil en problemas más complejos.
¿Qué pasa si no encuentro un número entero como resultado?
No te preocupes, un resultado decimal o fraccionario es completamente válido. Lo importante es que la relación proporcional se mantenga.
¿Dónde puedo aplicar el tercero proporcional en la vida diaria?
Hay muchas aplicaciones, desde ajustar recetas en la cocina hasta calcular precios en compras. ¡La clave es ver las relaciones en las cantidades que usas a diario!
Espero que esta guía te haya ayudado a comprender cómo calcular el tercero proporcional y su utilidad en diversas situaciones. No dudes en practicar con diferentes números y ver cómo funciona. ¡La práctica hace al maestro!