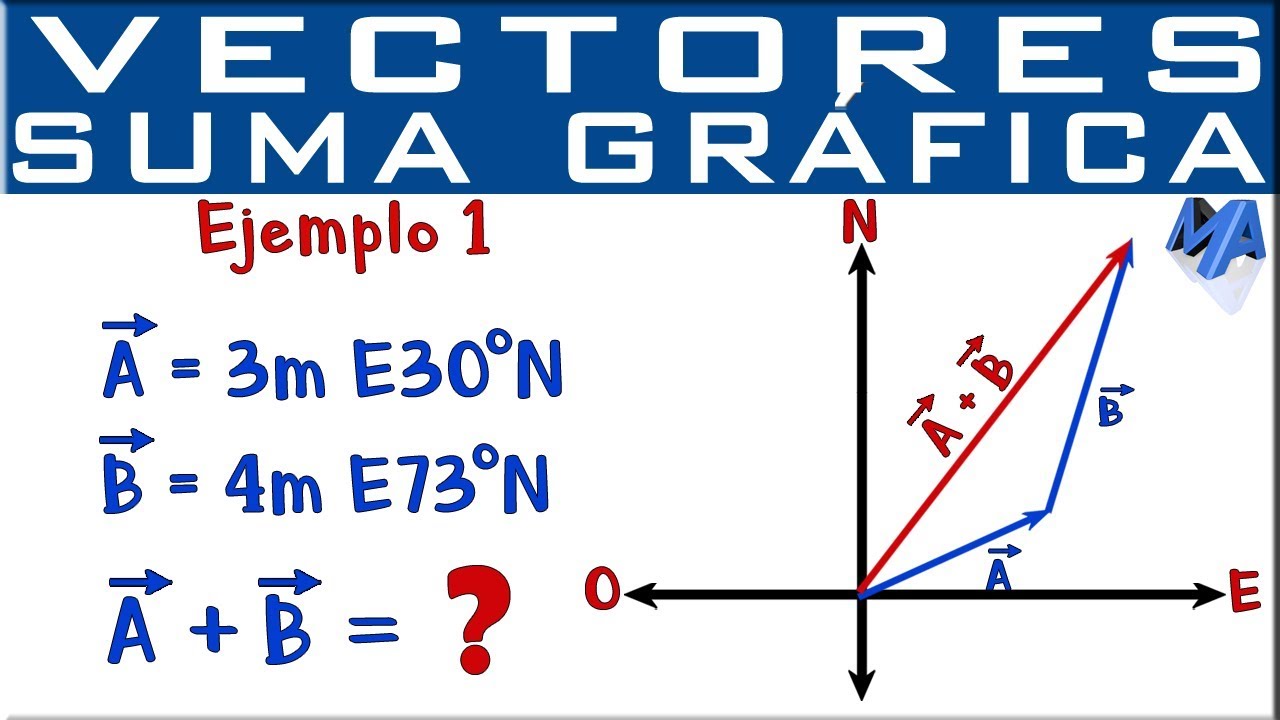
¿Por qué es Importante Comprender la Suma de Vectores?
La suma de vectores puede parecer un tema complicado al principio, pero te aseguro que es más accesible de lo que piensas. Imagina que estás en un parque, y decides ir a visitar a un amigo que vive en una casa al norte. Sin embargo, en el camino, decides hacer una parada en una heladería que se encuentra un poco al este. ¿Cómo representas tu camino? Aquí es donde entran en juego los vectores. Cada movimiento que haces puede ser representado como un vector, y la suma de estos vectores te dará la dirección y distancia total de tu viaje. Así que, ¡vamos a desglosar esto!
Los vectores son herramientas matemáticas que representan magnitudes y direcciones. Al sumar vectores, no solo estamos sumando números; estamos combinando direcciones y longitudes, lo que nos permite visualizar situaciones en el mundo real. En este artículo, te guiaré a través de los conceptos básicos, las representaciones gráficas y cómo realizar cálculos de manera sencilla. ¿Listo para sumergirte en el mundo de los vectores? ¡Vamos allá!
¿Qué es un Vector?
Antes de entrar en la suma de vectores, es crucial entender qué es un vector. En términos simples, un vector es una flecha que tiene una dirección y una magnitud. Piensa en una flecha que apunta hacia el norte: la longitud de la flecha podría representar la distancia, mientras que la dirección indica hacia dónde vas. Por ejemplo, si estás navegando en un barco, el vector puede indicar hacia dónde debes ir y cuán rápido.
Los vectores se pueden representar en un plano cartesiano, donde el eje X representa la dirección horizontal y el eje Y la dirección vertical. Esto nos permite tener una referencia clara para visualizar movimientos. Cada vector puede ser descrito por sus componentes en estos ejes, lo que nos lleva a la siguiente pregunta: ¿cómo se suman estos vectores?
La Suma de Vectores: Método Gráfico
La forma más intuitiva de sumar vectores es mediante un método gráfico. Este método utiliza la representación visual de los vectores para combinarlos de manera efectiva. Así que, ¡agarra papel y lápiz y sigamos este proceso!
Dibuja el Primer Vector
Comienza dibujando tu primer vector en el plano cartesiano. Asegúrate de que esté en la dirección correcta y que la longitud sea proporcional a su magnitud. Por ejemplo, si tu primer vector tiene una magnitud de 4 unidades hacia el este, dibuja una flecha de 4 unidades en la dirección del eje X positivo.
Dibuja el Segundo Vector
Ahora, toma el segundo vector. Este vector se debe dibujar desde la punta del primer vector. Por ejemplo, si el segundo vector tiene una magnitud de 3 unidades hacia el norte, dibuja una flecha de 3 unidades desde el extremo de la primera flecha, en dirección al eje Y positivo.
Traza la Resultante
Finalmente, la suma de estos dos vectores se representa como una flecha que va desde el origen (el punto de inicio del primer vector) hasta la punta del segundo vector. Esta nueva flecha se llama vector resultante y representa la combinación de ambos vectores. La longitud y dirección de esta flecha te darán la distancia total y la dirección en la que debes ir para llegar a tu destino.
La Suma de Vectores: Método Algebraico
Ahora que hemos cubierto el método gráfico, pasemos a la suma de vectores mediante el método algebraico. Este método es especialmente útil cuando se trata de realizar cálculos más complejos o cuando se trabaja con vectores en dimensiones superiores.
Descomposición en Componentes
Para sumar vectores algebraicamente, primero debes descomponer cada vector en sus componentes. Por ejemplo, si tienes un vector A que se representa como A = (Ax, Ay) y un vector B como B = (Bx, By), debes identificar las magnitudes en las direcciones X e Y.
Suma de Componentes
Una vez que hayas descompuesto los vectores en sus componentes, simplemente suma las componentes correspondientes. Así, tendrás:
– Componente X total = Ax + Bx
– Componente Y total = Ay + By
Esto te dará un nuevo vector resultante C = (Cx, Cy), donde Cx es la suma de las componentes X y Cy es la suma de las componentes Y.
Magnitud y Dirección del Vector Resultante
Para encontrar la magnitud del vector resultante, utiliza el teorema de Pitágoras:
[ |C| = sqrt{Cx^2 + Cy^2} ]
Y para calcular la dirección, puedes usar la función tangente:
[ theta = tan^{-1}left(frac{Cy}{Cx}right) ]
Esto te dará un panorama completo de cómo se comportan tus vectores en el plano.
Ejemplos Prácticos de Suma de Vectores
Ahora que hemos cubierto los métodos, es momento de ver algunos ejemplos prácticos. Esto te ayudará a afianzar el conocimiento y a entender cómo aplicar lo que has aprendido.
Ejemplo 1: Suma de Vectores en el Plano
Supón que tienes dos vectores: A = (3, 4) y B = (1, 2). Usando el método algebraico:
– Componente X total: 3 + 1 = 4
– Componente Y total: 4 + 2 = 6
Por lo tanto, el vector resultante C = (4, 6). Ahora, para calcular la magnitud:
[ |C| = sqrt{4^2 + 6^2} = sqrt{16 + 36} = sqrt{52} approx 7.21 ]
La dirección sería:
[ theta = tan^{-1}left(frac{6}{4}right) approx 56.31^circ ]
Ejemplo 2: Suma de Vectores en el Mundo Real
Imagina que estás conduciendo un coche. Primero te desplazas 50 km hacia el este y luego 30 km hacia el norte. Aquí tus vectores son:
– Vector A (50 km, 0 km)
– Vector B (0 km, 30 km)
Aplicando el método gráfico, dibujas tu primer vector hacia el este y luego desde su extremo, dibujas el segundo vector hacia el norte. La resultante sería la diagonal que conecta el inicio al final.
Al sumar algebraicamente:
– Componente X total: 50 + 0 = 50
– Componente Y total: 0 + 30 = 30
Magnitud:
[ |C| = sqrt{50^2 + 30^2} = sqrt{2500 + 900} = sqrt{3400} approx 58.31 ]
La dirección sería:
[ theta = tan^{-1}left(frac{30}{50}right) approx 30.96^circ ]
Aplicaciones de la Suma de Vectores
Entender la suma de vectores no es solo un ejercicio académico; tiene aplicaciones en diversas áreas. Desde la física hasta la ingeniería, la navegación y la informática, los vectores son fundamentales.
En la navegación, la suma de vectores es crucial. Cuando un barco navega, debe considerar la corriente del agua y el viento. Cada uno de estos factores puede representarse como vectores, y su suma determina la dirección y velocidad real del barco.
Física
En física, la suma de vectores se utiliza para calcular fuerzas. Si un objeto está sujeto a múltiples fuerzas, cada una puede representarse como un vector. La suma de estas fuerzas te dará la fuerza neta que actúa sobre el objeto, lo que es esencial para predecir su movimiento.
Informática y Gráficos por Computadora
En el mundo digital, la suma de vectores es fundamental en gráficos por computadora. Cada movimiento de un objeto en un entorno 3D puede describirse mediante vectores. La manipulación y la animación de estos objetos requieren una comprensión clara de cómo se suman y combinan los vectores.
La suma de vectores puede parecer intimidante al principio, pero como hemos visto, es un concepto accesible y valioso. Desde su representación gráfica hasta los cálculos algebraicos, dominar la suma de vectores te abre un mundo de posibilidades en matemáticas y ciencias aplicadas. ¿Te imaginas poder aplicar esto en tu vida diaria? Ya sea en la navegación, la física o incluso en tus videojuegos favoritos, los vectores están en todas partes.
¿Te has preguntado alguna vez cómo se relacionan los vectores con las fuerzas que experimentas en un juego? O quizás, ¿cómo un piloto de avión calcula su ruta? La suma de vectores es la clave para entender muchos fenómenos en el mundo que nos rodea. Así que la próxima vez que veas una flecha, recuerda que detrás de ella hay un mundo de matemáticas esperando ser explorado.
¿Los vectores siempre se representan en dos dimensiones?
No, los vectores pueden existir en tres dimensiones o más. En tres dimensiones, se añaden componentes en el eje Z. Sin embargo, para simplificar, a menudo trabajamos en dos dimensiones.
¿Puedo sumar vectores que tienen diferentes unidades?
No, para sumar vectores, deben tener las mismas unidades. Por ejemplo, no puedes sumar metros con kilómetros directamente; primero debes convertirlos a la misma unidad.
¿Cómo sé si debo usar el método gráfico o algebraico?
Si trabajas con vectores simples y quieres una representación visual, el método gráfico es ideal. Si necesitas precisión o estás trabajando con vectores en dimensiones superiores, el método algebraico es más efectivo.
¿Existen herramientas que me ayuden a sumar vectores?
Sí, hay software y aplicaciones que pueden ayudarte a visualizar y calcular la suma de vectores. Programas como GeoGebra o incluso calculadoras gráficas son excelentes para esto.
¿Puedo aplicar la suma de vectores en la vida cotidiana?
¡Absolutamente! La suma de vectores se aplica en diversas situaciones cotidianas, como calcular desplazamientos, navegar o incluso en deportes donde se requieren direcciones y magnitudes precisas. ¡Es un concepto más útil de lo que imaginas!