¿Alguna vez te has encontrado con un problema que parece tener múltiples soluciones? Eso es exactamente lo que ocurre en un sistema de inecuaciones. A diferencia de las ecuaciones, donde buscamos una única respuesta, aquí estamos lidiando con un conjunto de soluciones que cumplen ciertas condiciones. En este artículo, vamos a desglosar el concepto de sistemas de inecuaciones con dos incógnitas, cómo resolverlos y algunos ejemplos prácticos que te ayudarán a entender mejor el tema. Así que, si te sientes un poco perdido, ¡no te preocupes! Estamos aquí para hacer que este viaje sea más claro y emocionante.
¿Qué son las Inecuaciones?
Primero, aclaremos qué es una inecuación. Una inecuación es una relación matemática que indica que un valor es mayor o menor que otro. Por ejemplo, cuando decimos que (x > 5), estamos estableciendo que (x) debe ser un número mayor que 5. Ahora, cuando hablamos de un sistema de inecuaciones, nos referimos a un conjunto de dos o más inecuaciones que comparten las mismas variables. Esto significa que debemos encontrar los valores que satisfacen todas las inecuaciones al mismo tiempo. ¿Te suena complicado? No te preocupes, lo desglosaremos paso a paso.
Componentes de un Sistema de Inecuaciones
Variables
En un sistema de inecuaciones con dos incógnitas, generalmente trabajamos con las variables (x) e (y). Estas variables son las que queremos resolver, y sus valores deben cumplir con las condiciones impuestas por las inecuaciones.
Inecuaciones
Las inecuaciones pueden ser de diferentes tipos: mayor que ((>)), menor que ((<)), mayor o igual que ((geq)), y menor o igual que ((leq)). Por ejemplo, un sistema típico podría ser:
- 1. (2x + y < 10)
- 2. (x – y geq 3)
Soluciones
La solución de un sistema de inecuaciones es el conjunto de puntos ((x, y)) que satisfacen todas las inecuaciones del sistema. Esto se representa gráficamente como una región en el plano cartesiano. Pero, ¿cómo encontramos esta región? ¡Vamos a verlo!
Resolviendo un Sistema de Inecuaciones Paso a Paso
Paso 1: Graficar cada inecuación
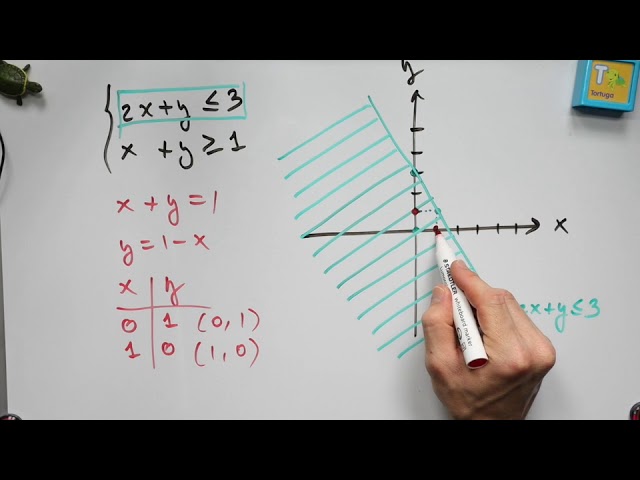
El primer paso para resolver un sistema de inecuaciones es graficar cada inecuación en el plano cartesiano. Para hacerlo, primero convertimos cada inecuación en una ecuación igualando a cero. Por ejemplo, para (2x + y < 10), graficamos la línea (2x + y = 10). Esta línea nos dará un límite que separa la región que satisface la inecuación de la que no lo hace.
Paso 2: Determinar la región de solución
Una vez que hemos graficado la línea, necesitamos determinar qué lado de la línea representa la solución de la inecuación. Para hacer esto, seleccionamos un punto de prueba que no esté en la línea, como ((0, 0)). Sustituyendo este punto en la inecuación, podemos ver si cumple o no. Si cumple, la región que contiene ese punto es la solución; si no, es la otra región.
Paso 3: Repetir para la siguiente inecuación
Ahora repetimos el proceso para la segunda inecuación. Graficamos la línea correspondiente y determinamos la región que satisface esa inecuación de la misma manera que hicimos antes.
Paso 4: Encontrar la intersección de las regiones
El paso final es encontrar la intersección de las regiones que hemos obtenido de cada inecuación. Esta intersección será la solución del sistema de inecuaciones. Recuerda, puede ser un área en el plano, un punto o incluso no haber solución en absoluto.
Ejemplo Práctico
Para ilustrar mejor este proceso, veamos un ejemplo práctico. Supongamos que tenemos el siguiente sistema de inecuaciones:
- 1. (x + y < 5)
- 2. (x – y > 1)
Graficando la primera inecuación
Comenzamos con (x + y = 5). Esta es una línea recta que intercepta el eje (y) en 5 y el eje (x) en 5 también. Ahora, para (x + y < 5), elegimos el punto de prueba ((0, 0)). Al sustituir, (0 + 0 < 5) es verdadero, por lo que la región que incluye ((0, 0)) es la solución.
Graficando la segunda inecuación
Ahora, graficamos (x – y = 1). Esta línea tiene una pendiente de 1 y cruza el eje (y) en -1. Al probar el punto ((0, 0)), encontramos que (0 – 0 > 1) es falso, así que la región que contiene ((0, 0)) no es la solución. Por lo tanto, la solución está en la parte opuesta de la línea.
Encontrando la intersección
Finalmente, la solución del sistema será la intersección de las dos regiones que hemos encontrado. Esto se verá como un área delimitada en el plano cartesiano, y cualquier punto dentro de esa área será una solución válida para nuestro sistema de inecuaciones.
¿Por Qué Son Importantes los Sistemas de Inecuaciones?
Los sistemas de inecuaciones no solo son una parte fundamental de las matemáticas, sino que también tienen aplicaciones en la vida real. Desde la economía hasta la ingeniería, estos sistemas nos permiten modelar situaciones donde hay múltiples condiciones que deben cumplirse. Por ejemplo, un agricultor podría usar inecuaciones para determinar cuántos acres de diferentes cultivos plantar, asegurándose de no exceder ciertos límites de recursos como agua o espacio.
Consejos para Resolver Sistemas de Inecuaciones
- Practica con ejemplos variados: Cuanto más practiques, más cómodo te sentirás con el proceso.
- Verifica tus respuestas: Después de encontrar la solución, siempre es bueno comprobar que los puntos satisfacen todas las inecuaciones.
- Usa herramientas gráficas: Si te resulta complicado graficar a mano, considera usar software de gráficos para visualizar mejor las soluciones.
¿Qué pasa si las inecuaciones no tienen solución?
Si no hay intersección entre las regiones de solución, significa que no hay ningún conjunto de valores que satisfaga todas las inecuaciones simultáneamente. En este caso, decimos que el sistema es inconsistente.
¿Cómo puedo comprobar si un punto es solución del sistema?
Simplemente sustituye las coordenadas del punto en cada inecuación. Si el punto cumple con todas, entonces es una solución del sistema.
¿Es lo mismo un sistema de ecuaciones que un sistema de inecuaciones?
No exactamente. En un sistema de ecuaciones, buscamos un punto o conjunto de puntos que satisfacen todas las ecuaciones de forma exacta. En un sistema de inecuaciones, buscamos un conjunto de puntos que cumplen con condiciones de desigualdad.
¿Se pueden tener más de dos incógnitas en un sistema de inecuaciones?
¡Claro que sí! Puedes tener sistemas con tres o más incógnitas. Sin embargo, la representación gráfica se vuelve más complicada, ya que las soluciones se extienden a dimensiones superiores.
¿Cuáles son algunas aplicaciones prácticas de los sistemas de inecuaciones?
Se utilizan en diversas áreas, como la optimización de recursos en la agricultura, la planificación de proyectos en ingeniería y la economía para modelar restricciones de producción o presupuesto.
Ahora que tienes una comprensión más clara sobre los sistemas de inecuaciones con dos incógnitas, ¿estás listo para poner en práctica lo que has aprendido? Recuerda, la clave está en la práctica y en no tener miedo de cometer errores. ¡Sigue explorando y resolviendo!