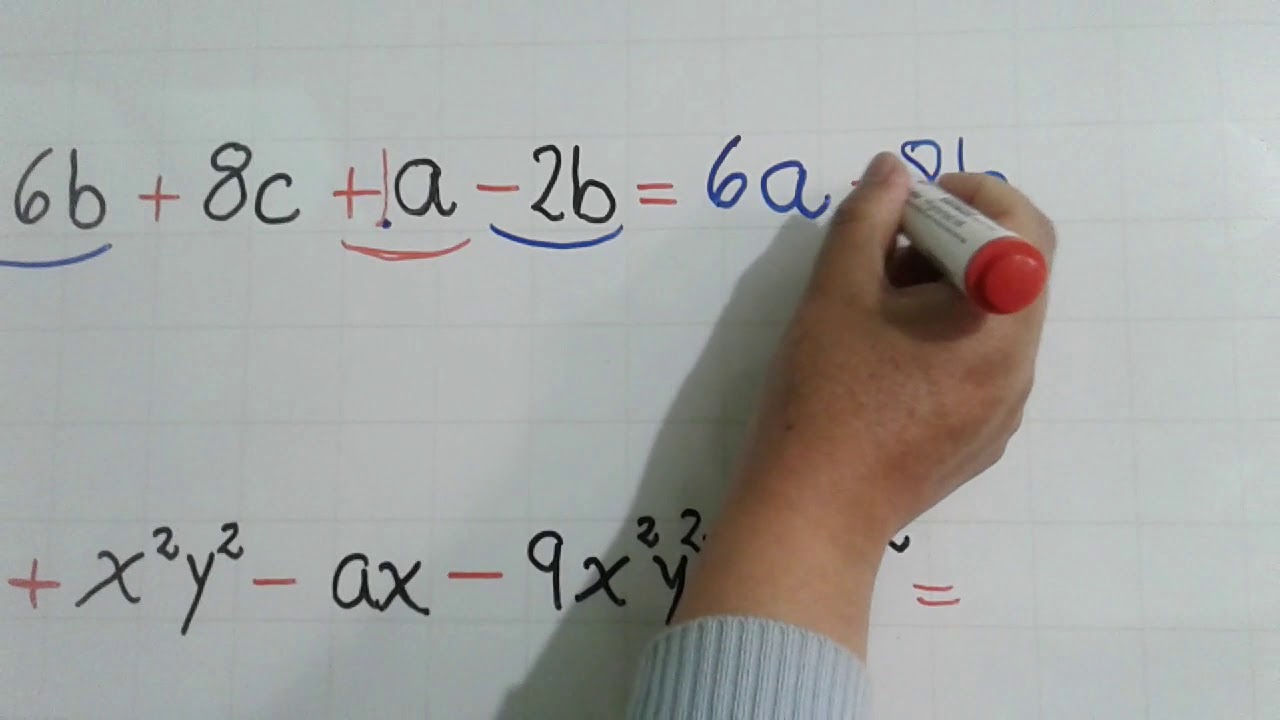¿Alguna vez te has encontrado frente a una montaña de términos en un polinomio y no sabes por dónde empezar? No te preocupes, ¡no estás solo! Reducir polinomios puede parecer complicado al principio, pero es como organizar un armario lleno de ropa: solo necesitas un poco de estrategia y paciencia. En esta guía, te llevaré paso a paso por el proceso de simplificación de expresiones matemáticas, asegurándome de que entiendas cada parte del camino. Así que, prepárate para deshacerte del desorden y encontrar claridad en el mundo de los polinomios.
¿Qué es un Polinomio?
Primero, aclaremos qué es un polinomio. Un polinomio es una expresión matemática que se compone de variables y coeficientes, combinados mediante operaciones de suma, resta y multiplicación. Por ejemplo, 2x² + 3x – 5 es un polinomio de segundo grado. Las partes individuales de un polinomio se llaman «términos». Entender esto es fundamental, ya que el primer paso para reducir un polinomio es identificar sus términos.
Identificando los Términos
Para reducir un polinomio, primero necesitas descomponerlo. Imagina que estás haciendo una ensalada: necesitas separar cada ingrediente antes de mezclarlos. Así que, ¿cómo identificamos los términos? Busca cada parte de la expresión que se une mediante un signo de suma o resta. En el ejemplo anterior, los términos son 2x², 3x y -5. Ahora que los tenemos identificados, ¡vamos a la siguiente etapa!
Combinar Términos Similares
Una de las técnicas más poderosas para reducir polinomios es combinar términos similares. Pero, ¿qué son los términos similares? Son aquellos que tienen la misma variable elevada a la misma potencia. Piensa en ellos como los pares de calcetines que buscas en tu cajón. Por ejemplo, en 2x² + 3x – 5 + 4x² – 2x, los términos 2x² y 4x² son similares, al igual que 3x y -2x.
Ejemplo de Combinación de Términos
Tomemos el polinomio 2x² + 3x – 5 + 4x² – 2x. Primero, agrupamos los términos similares:
- Términos de x²: 2x² + 4x² = 6x²
- Términos de x: 3x – 2x = 1x
- Término constante: -5
Así que, al combinar estos términos, obtenemos 6x² + 1x – 5. ¡Más fácil de manejar, verdad?
Factorización de Polinomios
Ahora que hemos reducido nuestra expresión, es hora de aprender sobre la factorización. Este proceso es como descomponer una pieza de rompecabezas en sus partes individuales para ver cómo encajan. La factorización nos ayuda a escribir un polinomio como el producto de otros polinomios. Por ejemplo, si tenemos x² – 5x + 6, podemos factorizarlo en (x – 2)(x – 3). Pero, ¿cómo lo hacemos?
Pasos para Factorizar un Polinomio
Para factorizar un polinomio cuadrático, sigue estos pasos:
- Identifica el polinomio en la forma estándar ax² + bx + c.
- Encuentra dos números que multipliquen a ac (el producto del coeficiente de x² y el término constante) y sumen b.
- Reescribe el polinomio utilizando esos dos números para dividir el término lineal.
- Factoriza por agrupación.
Suena complicado, pero con práctica, te volverás un experto.
Ejemplo Práctico de Factorización
Volvamos a nuestro ejemplo: x² – 5x + 6. Aquí, a = 1, b = -5 y c = 6. Entonces, ac = 1 * 6 = 6. Necesitamos encontrar dos números que sumen -5 y multipliquen a 6. Los números son -2 y -3.
Reescribimos el polinomio:
x² – 2x – 3x + 6
Ahora agrupamos:
(x² – 2x) + (-3x + 6)
Factorizamos cada grupo:
x(x – 2) – 3(x – 2)
Finalmente, sacamos el factor común:
(x – 2)(x – 3)
Uso de la Regla de Ruffini
Si te enfrentas a un polinomio de mayor grado, la regla de Ruffini puede ser tu mejor amiga. Es una técnica rápida para dividir polinomios y funciona especialmente bien cuando estás dividiendo por un binomio de la forma x – r. Imagina que es como cortar un pastel en porciones: ¡es más fácil de lo que parece!
¿Cómo Aplicar la Regla de Ruffini?
Para usar la regla de Ruffini, sigue estos pasos:
- Escribe los coeficientes del polinomio en una fila.
- Escribe el valor de r (la raíz) a la izquierda.
- Baja el primer coeficiente.
- Multiplica este coeficiente por r y súmalo al siguiente coeficiente.
- Repite hasta que hayas procesado todos los coeficientes.
¡Así de simple! Al final, tendrás el cociente y, si es necesario, el residuo.
Ejemplo de la Regla de Ruffini
Supongamos que queremos dividir 2x³ – 6x² + 2x – 4 entre x – 2. Los coeficientes son 2, -6, 2, -4 y el valor de r es 2.
Siguiendo los pasos:
- Coeficientes: 2, -6, 2, -4
- R: 2
Bajamos el primer coeficiente (2), luego multiplicamos por 2 y sumamos:
- Bajamos 2.
- 2 * 2 = 4; -6 + 4 = -2.
- -2 * 2 = -4; 2 – 4 = -2.
- -2 * 2 = -4; -4 – 4 = -8.
El resultado es 2x² – 2x – 2 con un residuo de -8. ¡Y ahí lo tienes!
¿Qué es un polinomio de grado superior?
Un polinomio de grado superior es aquel que tiene un término con una variable elevada a una potencia mayor que 2. Por ejemplo, x⁴ + 2x³ – 3x + 5 es un polinomio de cuarto grado.
¿Puedo reducir un polinomio con fracciones?
¡Claro que sí! Puedes trabajar con fracciones en los coeficientes de los términos. Simplemente sigue los mismos pasos: identifica, combina y factoriza.
¿Qué pasa si no encuentro términos similares?
No te preocupes si no encuentras términos similares. Si cada término es único, tu polinomio ya está en su forma más simple. A veces, menos es más.
¿Cuál es la diferencia entre un polinomio y un monomio?
Un monomio es una expresión matemática que tiene solo un término, mientras que un polinomio tiene dos o más. Por ejemplo, 3x es un monomio, y 2x² + 3x es un polinomio.
¿La factorización siempre es posible?
No siempre. Algunos polinomios no se pueden factorizar en términos de números enteros o fracciones. Sin embargo, se pueden utilizar métodos numéricos o gráficos para encontrar raíces.
Reducir polinomios puede parecer un desafío, pero con práctica y paciencia, te convertirás en un experto. Recuerda, cada paso cuenta, así que no dudes en volver a repasar esta guía siempre que lo necesites. ¡Buena suerte!