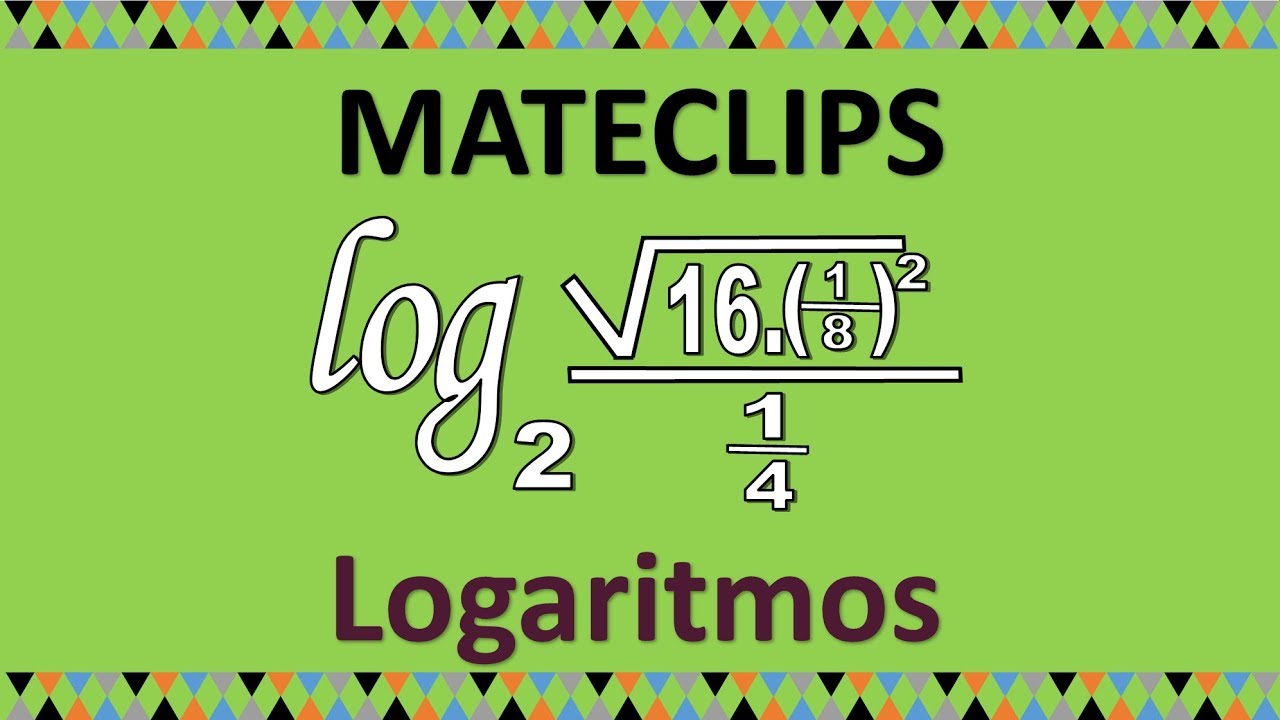Los logaritmos son una de esas cosas en matemáticas que, al principio, pueden parecer complicados, pero una vez que entiendes su esencia, ¡te das cuenta de lo útiles que son! Imagina que estás en una fiesta y, en lugar de tener que contar cada persona una por una, puedes simplemente usar una fórmula para calcular cuántas personas hay en total. Eso es, en esencia, lo que hacen los logaritmos: simplifican cálculos complicados. En este artículo, vamos a sumergirnos en las propiedades de los logaritmos, y lo mejor de todo es que al final podrás descargar un PDF completo con toda esta información. Así que, ¡vamos al grano!
¿Qué es un Logaritmo?
Antes de adentrarnos en las propiedades, es fundamental entender qué es un logaritmo. En términos simples, un logaritmo responde a la pregunta: ¿a qué potencia debemos elevar un número base para obtener otro número? Por ejemplo, si tenemos 10 como base y queremos saber a qué potencia debemos elevarlo para obtener 100, la respuesta es 2, porque 10 elevado a la 2 es 100. Así que, podemos decir que el logaritmo en base 10 de 100 es 2, o de manera más formal, log10(100) = 2.
Propiedades Básicas de los Logaritmos
Ahora que tenemos una idea básica de qué son los logaritmos, hablemos de sus propiedades. Estas propiedades son como las reglas del juego; si las conoces, te será mucho más fácil jugar. Vamos a desglosarlas una a una.
Propiedad del Producto
La primera propiedad que debes conocer es la del producto. Esta propiedad dice que el logaritmo de un producto es igual a la suma de los logaritmos de los factores. En términos matemáticos, esto se expresa como:
logb(xy) = logb(x) + logb(y)
Imagina que estás en una cocina y tienes que mezclar dos recetas. En lugar de hacer cada receta por separado y luego sumarlas, puedes pensar en la receta total como una combinación. Así, si estás multiplicando ingredientes, puedes simplemente sumar sus logaritmos.
Propiedad del Cociente
La segunda propiedad se refiere a la división. Aquí, el logaritmo de un cociente es igual a la resta de los logaritmos. Matemáticamente, se expresa así:
logb(x/y) = logb(x) - logb(y)
Piensa en esto como si estuvieras separando una pizza. Si tienes una pizza grande y decides dividirla entre tus amigos, puedes calcular cuánta pizza le toca a cada uno restando las porciones que ya han sido servidas. ¡Así de sencillo!
Propiedad de la Potencia
La tercera propiedad es la de la potencia. Esta propiedad establece que el logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base. Es decir:
logb(xn) = n * logb(x)
Imagina que tienes un amigo que siempre multiplica su energía por un factor cuando hace ejercicio. Si sabes cuánto rinde en un nivel, puedes calcular su rendimiento a niveles más altos multiplicando por ese factor. Así funcionan los logaritmos de las potencias.
Aplicaciones de los Logaritmos
Ahora que conoces las propiedades básicas, ¿te has preguntado dónde se utilizan los logaritmos en la vida real? Te sorprendería saber cuán presentes están en tu día a día.
Ciencias Naturales
Los logaritmos son fundamentales en campos como la química y la biología. Por ejemplo, en química, la escala de pH se basa en logaritmos. Un pH de 7 es neutro, pero cada unidad de cambio en pH representa un cambio de diez veces en acidez. ¡Eso es poder logarítmico!
Tecnología y Programación
Si alguna vez has oído hablar de algoritmos, probablemente has oído sobre la «complejidad logarítmica». Muchos algoritmos de búsqueda, como los que se utilizan en bases de datos, se basan en logaritmos para optimizar su rendimiento. Así que, si sueñas con ser un programador, ¡los logaritmos serán tus amigos!
Finanzas
En el mundo de las finanzas, los logaritmos también juegan un papel crucial. Por ejemplo, cuando se calcula el interés compuesto, a menudo se utilizan logaritmos para determinar el tiempo necesario para alcanzar una inversión determinada. ¡Así que ya sabes, cada vez que revisas tu estado de cuenta, los logaritmos están ahí!
Ejercicios Prácticos para Dominar los Logaritmos
Ahora que ya tienes una buena base sobre los logaritmos y sus propiedades, es hora de poner a prueba tus conocimientos. Aquí te dejo algunos ejercicios prácticos.
Ejercicio 1
Calcula el siguiente logaritmo utilizando la propiedad del producto:
log10(1000) = log10(10 * 100)
Ejercicio 2
Utiliza la propiedad del cociente para resolver:
log2(32/8)
Ejercicio 3
Usa la propiedad de la potencia para resolver:
log5(25)
Recuerda, practicar es la clave para dominar cualquier concepto matemático. Si te atascas, no dudes en volver a repasar las propiedades que hemos discutido.
Los logaritmos son más que una simple herramienta matemática; son un puente que conecta conceptos complejos de una manera más comprensible. Al dominar sus propiedades, no solo te vuelves más competente en matemáticas, sino que también te preparas para enfrentar desafíos en diversas disciplinas. Así que no subestimes el poder de los logaritmos. Y recuerda, si quieres tener todo este conocimiento a mano, ¡descarga el PDF completo que hemos preparado para ti!
¿Por qué son importantes los logaritmos?
Los logaritmos son esenciales porque simplifican cálculos complejos, especialmente en ciencias, tecnología y finanzas. Son una herramienta fundamental para resolver problemas en diversas disciplinas.
¿Los logaritmos solo se utilizan en matemáticas?
No, los logaritmos se utilizan en muchas áreas, como la química (pH), la biología (crecimiento poblacional), la programación (algoritmos) y las finanzas (interés compuesto).
¿Cómo puedo mejorar mi comprensión de los logaritmos?
La práctica es clave. Realiza ejercicios, utiliza aplicaciones interactivas y no dudes en pedir ayuda cuando lo necesites. Además, puedes descargar nuestro PDF para tener un recurso completo a mano.
¿Qué debo hacer si me confundo con las propiedades de los logaritmos?
Si te confundes, revisa cada propiedad por separado y practica con ejemplos. A veces, hacer una pausa y volver a mirar el concepto con una mente fresca puede ayudarte a aclarar las cosas.