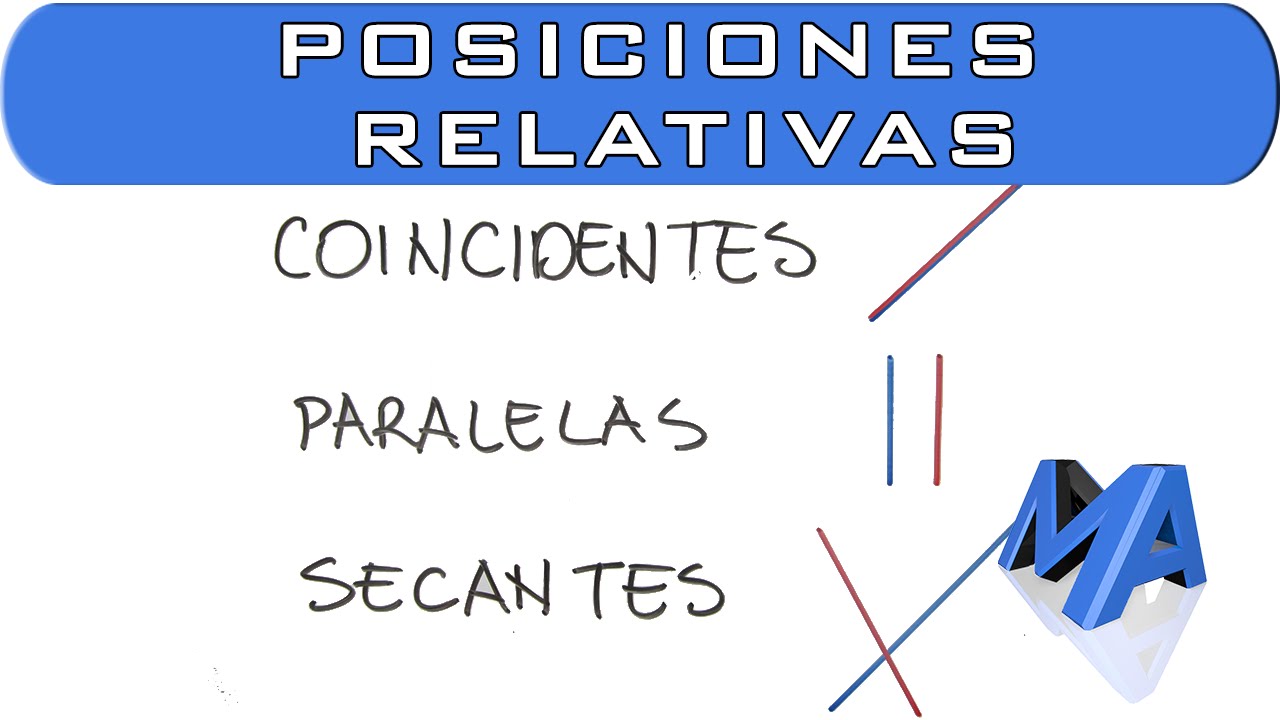
Entendiendo la Relación entre Rectas
¿Alguna vez te has preguntado cómo interactúan las rectas en el plano? Es un tema que puede parecer complicado al principio, pero en realidad es bastante interesante y tiene aplicaciones prácticas en muchos campos, desde la arquitectura hasta la programación. La posición relativa de las rectas se refiere a cómo se ubican unas respecto a otras. Pueden ser paralelas, secantes o coincidentes, y cada una de estas relaciones tiene sus propias características y consecuencias. En este artículo, vamos a desglosar cada uno de estos tipos, ofrecer ejemplos claros y explorar sus aplicaciones en la vida cotidiana. Así que, si estás listo para adentrarte en el mundo de las matemáticas geométricas, ¡vamos a ello!
## Tipos de Posición Relativa de Rectas
Cuando hablamos de la posición relativa de rectas, generalmente nos referimos a tres tipos principales: paralelas, secantes y coincidentes. Cada una tiene sus propias particularidades y es fundamental entenderlas para aplicar correctamente los conceptos en problemas más complejos.
### Rectas Paralelas
Las rectas paralelas son aquellas que nunca se cruzan, no importa cuánto se extiendan. Imagina dos vías de tren que se extienden hacia el horizonte; nunca se encontrarán, a menos que cambien de dirección. En términos matemáticos, dos rectas son paralelas si tienen la misma pendiente. Por ejemplo, si tenemos las ecuaciones y = 2x + 3 y y = 2x – 5, ambas tienen una pendiente de 2, lo que significa que son paralelas.
Las rectas paralelas son esenciales en la arquitectura y el diseño, ya que aseguran que las estructuras sean estables y visualmente agradables. Además, en el mundo del arte, la perspectiva se basa en la idea de paralelismo para crear profundidad en las obras.
### Rectas Secantes
Ahora, hablemos de las rectas secantes. Estas son las que se cruzan en un punto, creando un ángulo. Piensa en dos caminos que se encuentran en una intersección; en ese punto, ambas rectas se cruzan. Matemáticamente, si tenemos las ecuaciones y = x + 1 y y = -x + 4, podemos ver que se cruzan en el punto (1.5, 2.5). La intersección es un concepto importante en muchas áreas, como en la resolución de sistemas de ecuaciones.
Las rectas secantes son utilizadas en diversas aplicaciones, desde la navegación hasta la programación de gráficos en 2D. Comprender cómo interactúan es clave para resolver problemas en estos campos.
### Rectas Coincidentes
Por último, pero no menos importante, están las rectas coincidentes. Estas rectas son, esencialmente, la misma línea, ocupando el mismo espacio en el plano. Si tienes dos ecuaciones que representan la misma recta, como y = 3x + 2 y 2y = 6x + 4 (que es simplemente una versión escalada de la primera), entonces esas rectas son coincidentes.
Este concepto es especialmente relevante en álgebra y geometría, ya que nos ayuda a simplificar problemas y encontrar soluciones más fácilmente. En la práctica, las rectas coincidentes pueden aparecer en situaciones donde se busca resolver problemas de optimización.
## Ejemplos Prácticos
Vamos a ver algunos ejemplos más concretos para entender mejor estos conceptos.
### Ejemplo de Rectas Paralelas
Supongamos que estamos diseñando un parque. Necesitamos colocar caminos que no se crucen. Si decidimos que los caminos tengan una pendiente de 1, nuestras ecuaciones podrían ser y = x + 2 y y = x – 3. Ambas ecuaciones tienen la misma pendiente, lo que significa que los caminos nunca se cruzarán, manteniendo la seguridad y la fluidez del tránsito en el parque.
### Ejemplo de Rectas Secantes
Imagina que estás organizando un evento y necesitas planificar las diferentes áreas del lugar. Si tienes un escenario en un extremo y una zona de comida en el otro, puedes representar estas áreas con rectas secantes. Por ejemplo, las ecuaciones y = 2x + 1 y y = -0.5x + 5 pueden representar estas áreas. La intersección de estas dos rectas será el punto donde se pueden conectar, facilitando el flujo de personas.
### Ejemplo de Rectas Coincidentes
Volviendo al diseño del parque, imagina que decides agregar una zona de juegos que ya está representada por una de tus rectas. Si decides que esa zona se amplíe y creas otra ecuación que represente la misma área, tendrás rectas coincidentes. Por ejemplo, si la zona de juegos está representada por y = 2x + 1, y decides que la ampliación es exactamente la misma, tendrás otra ecuación, digamos, 2y = 4x + 2. Ambas ecuaciones representan la misma área de juegos.
## Aplicaciones en la Vida Real
La posición relativa de rectas no solo es un tema teórico; tiene aplicaciones prácticas en el mundo real. Veamos algunas áreas donde estos conceptos son especialmente útiles.
### Diseño Gráfico
En el diseño gráfico, entender cómo se relacionan las líneas puede ayudar a crear composiciones visuales atractivas. Las líneas paralelas pueden dar una sensación de estabilidad, mientras que las líneas secantes pueden agregar dinamismo y movimiento a una obra. Además, el uso de líneas coincidentes puede simplificar el diseño, haciendo que los elementos se vean más organizados.
### Ingeniería y Arquitectura
En la ingeniería y la arquitectura, el diseño de estructuras a menudo implica trabajar con líneas y ángulos. Las rectas paralelas son cruciales para asegurar que las estructuras sean estables, mientras que las secantes pueden ser necesarias para crear intersecciones funcionales. Además, la identificación de líneas coincidentes puede ayudar a simplificar cálculos y mejorar la eficiencia del diseño.
### Programación y Desarrollo de Juegos
En la programación, especialmente en el desarrollo de juegos, las rectas secantes son esenciales para detectar colisiones entre objetos. Por ejemplo, si un personaje se mueve a través de un entorno, el juego necesita saber cuándo ese personaje se encuentra con un obstáculo. Aquí es donde las matemáticas de las rectas entran en juego, permitiendo que los desarrolladores creen experiencias de juego más realistas.
## Conclusión
Ahora que hemos explorado la posición relativa de rectas y su importancia en diversas áreas, es evidente que estos conceptos son más que simples líneas en un plano. Son herramientas poderosas que nos ayudan a entender y diseñar nuestro entorno. Desde la arquitectura hasta el arte y la programación, el conocimiento de cómo interactúan las rectas puede llevar a soluciones innovadoras y efectivas.
### Preguntas Frecuentes
¿Qué sucede si dos rectas tienen pendientes diferentes?
Cuando dos rectas tienen pendientes diferentes, se cruzarán en un punto, es decir, son secantes.
¿Cómo puedo saber si dos rectas son paralelas solo con sus ecuaciones?
Si las ecuaciones de las rectas tienen la misma pendiente y diferentes interceptos, son paralelas.
¿Dónde se utilizan las rectas coincidentes en la vida real?
Las rectas coincidentes pueden aparecer en situaciones de optimización y simplificación en diseño y resolución de problemas.
¿Puedo tener más de dos rectas secantes?
Sí, puedes tener múltiples rectas secantes que se crucen en diferentes puntos, creando una red compleja de intersecciones.
¿Cómo se relaciona la posición relativa de rectas con la geometría analítica?
La posición relativa de rectas es un concepto clave en la geometría analítica, que utiliza coordenadas y ecuaciones para describir la relación entre diferentes figuras geométricas.