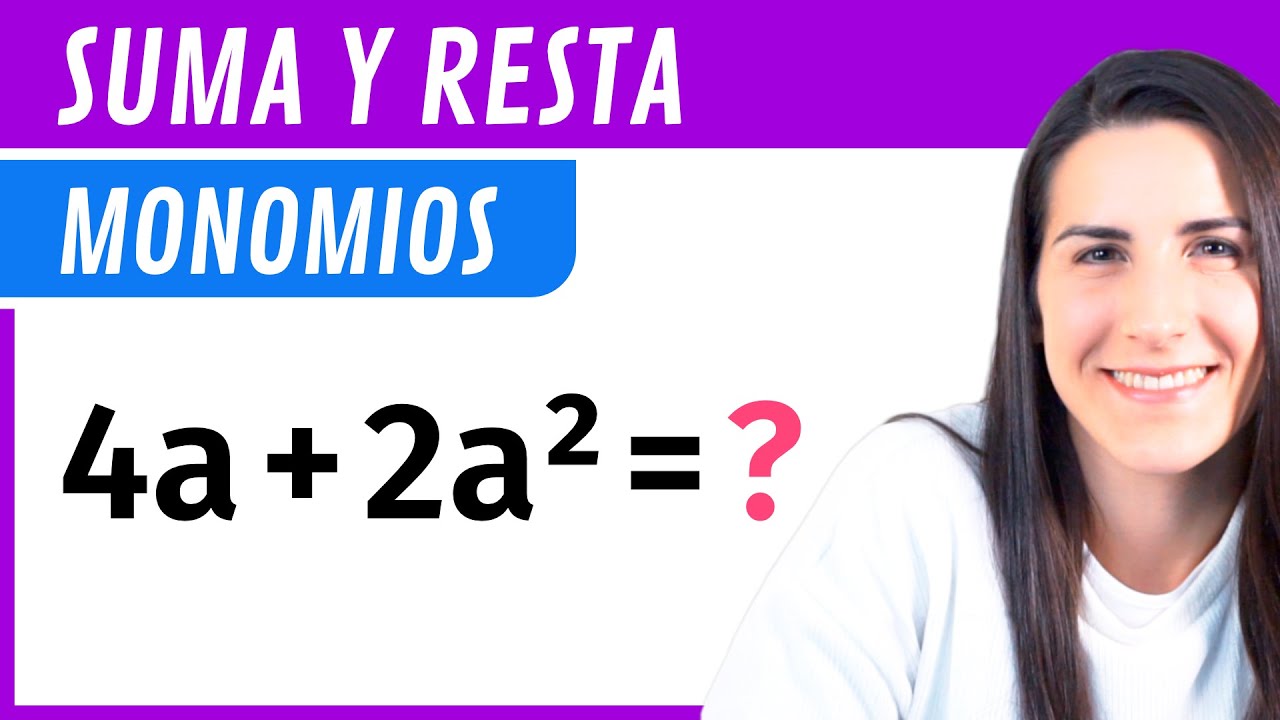¡Hola! Si estás aquí, es porque quieres entender mejor los monomios y cómo operarlos, ¿verdad? Bueno, estás en el lugar correcto. Vamos a desglosar este tema paso a paso, y te prometo que no será aburrido. Imagina que los monomios son como los bloques de construcción de las matemáticas. Al aprender a manejarlos, podrás construir estructuras más complejas, como polinomios y ecuaciones. Pero primero, vamos a asegurarnos de que tengas una buena base. ¿Listo? ¡Vamos a ello!
¿Qué es un Monomio?
Comencemos por lo básico. Un monomio es una expresión algebraica que consta de un solo término. ¿Qué significa eso? Bueno, un monomio puede incluir números, letras y exponentes, pero nunca se pueden sumar o restar otros términos dentro de él. Por ejemplo, 3x² es un monomio. Aquí, 3 es el coeficiente (el número que multiplica a la variable), x es la variable y 2 es el exponente que indica cuántas veces se multiplica la variable por sí misma. Así que, si lo piensas, un monomio es como una pequeña familia: tiene su propio número (coeficiente) y su propio nombre (variable).
Tipos de Monomios
Los monomios pueden clasificarse de varias maneras. Vamos a ver algunos tipos comunes:
Monomios Numéricos
Estos son aquellos que no tienen variables. Por ejemplo, 5 o -12 son monomios numéricos. Son como los soldados que marchan solos, sin necesidad de compañía.
Monomios con Variables
Estos son los más comunes y pueden tener diferentes variables. Por ejemplo, 4xy o -3a²b son monomios con variables. Aquí, las variables son como los compañeros de juego que hacen que la diversión sea aún mayor.
Monomios con Exponentes
Los exponentes nos dicen cuántas veces se multiplica la variable por sí misma. Por ejemplo, en 2x³, el 3 indica que x se multiplica por sí mismo tres veces. ¡Es como tener una fiesta donde cada invitado trae a más amigos!
Operaciones Básicas con Monomios
Ahora que tenemos una buena idea de qué son los monomios, hablemos de cómo operar con ellos. Hay tres operaciones principales que vamos a explorar: suma, resta y multiplicación. Recuerda, ¡la práctica hace al maestro!
Suma de Monomios
La suma de monomios solo se puede realizar si tienen las mismas variables y exponentes. Por ejemplo, si tienes 2x² + 3x², puedes sumarlos porque ambos son x². La suma sería 5x². Pero, si intentas sumar 2x² + 3x³, no puedes, ya que los exponentes son diferentes. ¡Es como intentar juntar manzanas y naranjas!
Ejercicio:
Intenta sumar los siguientes monomios: 4a² + 2a². ¿Cuál es la respuesta? ¡Correcto! Es 6a².
Resta de Monomios
La resta sigue las mismas reglas que la suma. Solo puedes restar monomios que tengan las mismas variables y exponentes. Por ejemplo, 5y³ – 2y³ es igual a 3y³. Pero, si intentas restar 5y³ – 2y², no podrás hacerlo. Recuerda, ¡solo puedes restar monomios que sean del mismo «tipo»!
Ejercicio:
¿Qué tal si restas estos monomios? 7m² – 3m². ¿Cuál es la respuesta? ¡Exacto! Es 4m².
Multiplicación de Monomios
La multiplicación es un poco más sencilla. Al multiplicar monomios, multiplicas los coeficientes y sumas los exponentes de las variables. Por ejemplo, si tienes 3x² * 2x³, multiplicas 3 y 2 para obtener 6 y sumas los exponentes: 2 + 3 = 5. Así que el resultado es 6x⁵. ¡Es como mezclar dos colores para crear uno nuevo!
Ejercicio:
Prueba multiplicar estos monomios: 4a² * 3a³. ¿Cuál es el resultado? ¡Correcto! Es 12a⁵.
Propiedades de los Monomios
Es importante conocer algunas propiedades de los monomios que te ayudarán a simplificar y resolver problemas más fácilmente. Aquí van algunas de ellas:
Propiedad Conmutativa
Esta propiedad dice que el orden en que sumas o multiplicas no afecta el resultado. Por ejemplo, 2 + 3 es lo mismo que 3 + 2. ¡Es como si pudieras jugar con tus bloques en cualquier orden y siempre obtendrás la misma torre!
Propiedad Asociativa
Esta propiedad dice que cuando sumas o multiplicas más de dos monomios, puedes agruparlos de cualquier manera. Por ejemplo, (2 + 3) + 4 es lo mismo que 2 + (3 + 4). ¡Es como si tuvieras un grupo de amigos y pudieras organizarlos en diferentes equipos, pero la diversión siempre es la misma!
Propiedad Distributiva
Esta propiedad es súper útil. Te dice que puedes multiplicar un monomio por una suma o resta. Por ejemplo, 2(a + b) se convierte en 2a + 2b. ¡Es como repartir caramelos entre tus amigos, asegurándote de que todos reciban su parte!
Ejercicios Prácticos
Ahora que hemos cubierto las operaciones y propiedades de los monomios, es hora de poner en práctica lo aprendido. Aquí te dejo algunos ejercicios para que puedas intentar resolverlos por tu cuenta:
Ejercicio 1:
Suma los siguientes monomios: 5x² + 7x² – 3x².
Ejercicio 2:
Resta los siguientes monomios: 10y³ – 4y³ + 2y³.
Ejercicio 3:
Multiplica los siguientes monomios: 6a² * 4a³.
Ejercicio 4:
Usa la propiedad distributiva en la siguiente expresión: 3(x + 4).
Soluciones a los Ejercicios
Ahora, vamos a revisar las soluciones de los ejercicios que te propuse:
Solución Ejercicio 1:
5x² + 7x² – 3x² = 9x².
Solución Ejercicio 2:
10y³ – 4y³ + 2y³ = 8y³.
Solución Ejercicio 3:
6a² * 4a³ = 24a⁵.
Solución Ejercicio 4:
3(x + 4) = 3x + 12.
Consejos para Aprender Monomios
Aprender sobre monomios puede parecer complicado al principio, pero aquí tienes algunos consejos para que el proceso sea más fácil y divertido:
- Practica Regularmente: La práctica constante te ayudará a dominar los conceptos. No dudes en buscar más ejercicios.
- Utiliza Recursos Visuales: Dibuja diagramas o usa colores para diferenciar los términos. A veces, ver las cosas de manera visual puede hacer que todo tenga más sentido.
- Forma Grupos de Estudio: Aprender con otros puede hacer que el proceso sea más entretenido. ¡Compartan sus conocimientos y resuelvan problemas juntos!
1. ¿Qué pasa si tengo diferentes variables en un monomio?
No puedes sumarlos ni restarlos. Por ejemplo, 2x y 3y no se pueden combinar, ya que son diferentes «tipos».
2. ¿Puedo tener monomios con exponentes negativos?
Sí, los exponentes negativos son válidos. Por ejemplo, 2x⁻² es un monomio, pero representa 1/(2x²).
3. ¿Cómo se simplifican los monomios con coeficientes fraccionarios?
La misma regla aplica. Solo multiplica o suma los coeficientes. Por ejemplo, 1/2x² + 1/3x² no se puede sumar directamente, pero puedes encontrar un denominador común.
4. ¿Qué son los polinomios y cómo se relacionan con los monomios?
Los polinomios son expresiones que contienen dos o más monomios. Así que, en cierto modo, ¡los monomios son los bloques de construcción de los polinomios!
Espero que esta guía te haya ayudado a entender mejor los monomios y cómo operarlos. Recuerda, la práctica es clave. ¡No dudes en seguir practicando y preguntando si tienes dudas! Hasta la próxima, ¡y feliz aprendizaje!