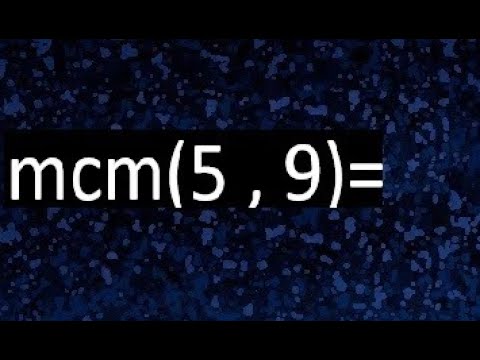¡Hola! Hoy vamos a sumergirnos en el fascinante mundo de las matemáticas, específicamente en el cálculo del Mínimo Común Múltiplo (MCM). ¿Alguna vez te has preguntado cómo dos números pueden encontrarse en un punto común cuando se multiplican? Bueno, el MCM es precisamente eso: el número más pequeño que es múltiplo de dos o más números. En este caso, vamos a calcular el MCM de 9 y 5. Pero no te preocupes, no necesitas ser un genio matemático para seguirme; lo vamos a desglosar paso a paso. Así que, ¡prepárate para convertirte en un experto en el MCM!
¿Qué es el Mínimo Común Múltiplo?
Antes de entrar en detalles, vamos a aclarar qué es exactamente el Mínimo Común Múltiplo. Imagina que tienes dos amigos, uno que llega a casa cada 9 días y otro que llega cada 5 días. El MCM sería el primer día en que ambos estarán en casa al mismo tiempo. En otras palabras, es el número más pequeño que puede ser dividido por ambos números sin dejar un residuo. ¿Te parece un concepto complicado? No te preocupes, es más sencillo de lo que parece.
¿Cómo se Calcula el Mínimo Común Múltiplo?
Ahora que sabemos qué es el MCM, pasemos a la parte emocionante: ¡calcularlo! Existen varios métodos para hacerlo, pero aquí vamos a utilizar uno de los más sencillos: el método de los múltiplos. Así que, si tienes una hoja y un lápiz a la mano, ¡sigue conmigo!
Método de los Múltiplos
Primero, vamos a listar los múltiplos de cada número. Comencemos con el 9:
- 9 x 1 = 9
- 9 x 2 = 18
- 9 x 3 = 27
- 9 x 4 = 36
- 9 x 5 = 45
Ahora, hagamos lo mismo con el 5:
- 5 x 1 = 5
- 5 x 2 = 10
- 5 x 3 = 15
- 5 x 4 = 20
- 5 x 5 = 25
- 5 x 6 = 30
- 5 x 7 = 35
- 5 x 8 = 40
- 5 x 9 = 45
Ahora que tenemos nuestras listas, busquemos el primer múltiplo que aparece en ambas. ¡Y ahí está! El número 45. Por lo tanto, el Mínimo Común Múltiplo de 9 y 5 es 45. ¿Ves? ¡No fue tan difícil!
Otra Forma de Calcular el Mínimo Común Múltiplo
Si bien el método de los múltiplos es bastante directo, hay otra técnica que puede ser útil, especialmente si trabajas con números más grandes: el método de la descomposición en factores primos. Este método puede parecer un poco más complejo, pero con un poco de práctica, se vuelve muy fácil.
Método de la Descomposición en Factores Primos
Para utilizar este método, primero necesitamos descomponer ambos números en sus factores primos. Vamos a empezar con el 9:
- 9 = 3 x 3 = 3²
Ahora, descomponemos el 5, que es un número primo:
- 5 = 5¹
Ahora, para encontrar el MCM, tomamos cada factor primo, elevándolo a la mayor potencia que aparece en la descomposición de ambos números. Así que, en nuestro caso, sería:
- 3² (de 9)
- 5¹ (de 5)
Multiplicamos estos factores: 3² x 5¹ = 9 x 5 = 45. ¡Voilà! De nuevo, llegamos a 45 como el MCM de 9 y 5. ¡Increíble, ¿verdad?
¿Por Qué Es Importante el Mínimo Común Múltiplo?
Ahora que hemos aprendido a calcular el MCM, quizás te estés preguntando: «¿Pero por qué debería importarme?» Bueno, el MCM tiene muchas aplicaciones prácticas en la vida cotidiana. Por ejemplo, es muy útil en problemas de programación de eventos, donde necesitas encontrar un momento en que dos actividades ocurren al mismo tiempo. También es esencial en fracciones, ya que te ayuda a encontrar un denominador común para sumarlas o restarlas. En resumen, entender el MCM puede hacer tu vida mucho más fácil en diversas situaciones.
Ejercicios Prácticos
Ahora que hemos cubierto la teoría y los métodos, ¿qué tal si practicamos un poco? Aquí tienes algunos ejercicios que puedes intentar:
- Calcula el MCM de 6 y 8.
- Calcula el MCM de 12 y 15.
- Calcula el MCM de 4 y 10.
Recuerda usar los métodos que hemos discutido. ¡Te sorprenderá lo fácil que se vuelve con la práctica!
Y ahí lo tienes, un recorrido completo por el Mínimo Común Múltiplo de 9 y 5. Desde qué es hasta cómo calcularlo y por qué es importante. Espero que te sientas más seguro con este concepto y que ahora puedas aplicarlo en diferentes situaciones. Recuerda, la práctica hace al maestro, así que no dudes en seguir practicando. ¿Te animas a compartir este artículo con un amigo que también necesita ayuda con el MCM?
¿El Mínimo Común Múltiplo siempre es mayor que ambos números?
En general, sí. El MCM de dos números siempre es mayor o igual que el número más grande de los dos. Sin embargo, hay excepciones cuando ambos números son iguales; en ese caso, el MCM es igual a ese número.
¿Qué pasa si uno de los números es cero?
Si uno de los números es cero, el MCM se considera indefinido. Esto se debe a que cualquier número multiplicado por cero es cero, lo que hace que no haya un múltiplo común que se pueda determinar.
¿Se puede calcular el MCM de más de dos números?
¡Absolutamente! El MCM se puede calcular para tres o más números utilizando los mismos métodos que hemos discutido. Simplemente necesitas encontrar los múltiplos o descomponer cada número en factores primos y luego seguir el mismo proceso.
¿El Mínimo Común Múltiplo es lo mismo que el Máximo Común Divisor?
No, son conceptos diferentes. El Mínimo Común Múltiplo se refiere al múltiplo más pequeño que dos o más números comparten, mientras que el Máximo Común Divisor es el número más grande que puede dividir a esos números sin dejar un residuo.
¿Dónde más puedo aplicar el MCM en la vida real?
Además de en problemas de programación de eventos, el MCM se utiliza en áreas como la planificación de horarios, la resolución de problemas de mezcla de ingredientes en recetas, y en muchas aplicaciones en álgebra y teoría de números. ¡Es un concepto realmente útil!