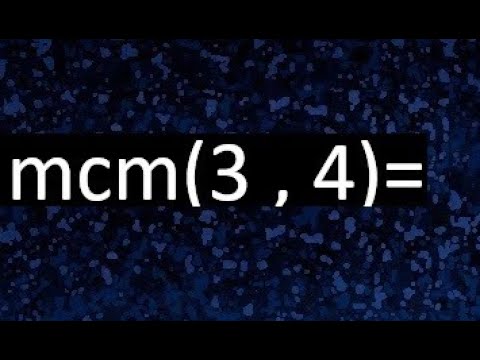¿Cómo calcular el mínimo común múltiplo de 3 y 4 de manera sencilla?

Entendiendo el Mínimo Común Múltiplo

Calcular el mínimo común múltiplo (MCM) puede parecer una tarea complicada al principio, pero te prometo que es más fácil de lo que parece. Imagina que tienes dos amigos, uno que solo sale a jugar cada 3 días y otro que lo hace cada 4 días. ¿Te has preguntado cuándo volverán a coincidir en el parque? Eso es exactamente lo que el MCM nos ayuda a encontrar. En este artículo, te guiaré a través de un proceso sencillo para calcular el MCM de 3 y 4, y te daré algunos trucos y consejos para que entiendas mejor este concepto matemático. Así que, si estás listo, ¡vamos a sumergirnos en el mundo de los múltiplos!

¿Qué es el Mínimo Común Múltiplo?

Primero, aclaremos qué es exactamente el Mínimo Común Múltiplo. El MCM de dos o más números es el múltiplo más pequeño que es común a todos ellos. En otras palabras, es el número más pequeño que puedes obtener al multiplicar cada uno de los números. Volviendo a nuestros amigos, el MCM sería el primer día en que ambos pueden jugar juntos. Para 3 y 4, tenemos que buscar los múltiplos de cada uno y ver cuál es el primero que se repite.

Múltiplos de 3 y 4

Comencemos listando los múltiplos de cada número. Para el número 3, los múltiplos son:

• 3, 6, 9, 12, 15, 18, …

Y para el número 4, los múltiplos son:

• 4, 8, 12, 16, 20, …

Ahora, observa las listas. ¿Ves algún número que se repita? ¡Exacto! El 12 es el primer número que aparece en ambas listas. Por lo tanto, el MCM de 3 y 4 es 12. Es como encontrar un punto de encuentro en el parque donde ambos amigos pueden coincidir. ¡Fácil, verdad?

Otra forma de calcular el MCM: el método de descomposición en factores primos

Ahora que hemos visto cómo encontrar el MCM de manera directa, hablemos de otro método que puede ser útil: la descomposición en factores primos. Este método puede parecer un poco más técnico, pero una vez que lo entiendes, es muy útil. La idea es descomponer cada número en sus factores primos y luego utilizar estos factores para encontrar el MCM.

Descomponiendo 3 y 4 en factores primos

Para el número 3, la única forma de descomponerlo es en sí mismo, ya que es un número primo:

• 3 = 3

Ahora, para el número 4, podemos descomponerlo así:

• 4 = 2 × 2 = 2²

Ahora, tomamos todos los factores primos que hemos encontrado. Necesitamos el mayor exponente de cada factor primo que aparece en la descomposición:

• Para el 3, tenemos 3¹
• Para el 2, tenemos 2²

El MCM se calcula multiplicando estos factores primos con sus mayores exponentes:

MCM = 2² × 3¹ = 4 × 3 = 12

Así que, usando este método, también llegamos a que el MCM de 3 y 4 es 12. ¡Increíble, ¿verdad? Esta técnica es especialmente útil cuando trabajamos con números más grandes o cuando tenemos más de dos números!

Ejemplos prácticos para entender mejor

Ahora que hemos cubierto cómo calcular el MCM, veamos algunos ejemplos prácticos. ¿Por qué no intentar calcular el MCM de otros números juntos? Por ejemplo, ¿qué tal 6 y 8? Primero, listamos los múltiplos:

Múltiplos de 6 y 8

Los múltiplos de 6 son:

• 6, 12, 18, 24, …

Y los múltiplos de 8 son:

• 8, 16, 24, …

Si observas, el primer múltiplo común es 24. Por lo tanto, el MCM de 6 y 8 es 24. Si utilizamos el método de descomposición en factores primos:

• 6 = 2 × 3
• 8 = 2 × 2 × 2 = 2³

Entonces, tomamos los factores primos y sus mayores exponentes:

• 2³
• 3¹

MCM = 2³ × 3¹ = 8 × 3 = 24. ¡Así que el MCM de 6 y 8 también es 24!

Aplicaciones del Mínimo Común Múltiplo

Ahora que ya sabes cómo calcular el MCM, quizás te estés preguntando, ¿para qué sirve esto en la vida real? El MCM tiene varias aplicaciones prácticas. Por ejemplo, es útil en la planificación de eventos, programación de turnos, y hasta en situaciones cotidianas como repartir cosas de manera equitativa.

Planificación de eventos

Imagina que organizas un evento donde dos grupos diferentes tienen horarios de reunión distintos. Uno se reúne cada 5 días y el otro cada 8 días. Para saber cuándo ambos grupos pueden reunirse al mismo tiempo, necesitarás calcular el MCM de 5 y 8. Al hacerlo, descubrirás que se reunirán cada 40 días, lo que te permitirá planificar mejor el evento.

Reparto equitativo

Otra aplicación sería en el reparto de golosinas. Si tienes 12 caramelos y 8 galletas y quieres repartirlos equitativamente entre un grupo de amigos, el MCM te ayudará a saber cuántos amigos pueden recibir una porción igual. En este caso, sería 24, lo que significa que podrías repartir de manera justa si tienes 24 amigos.

¿El MCM siempre es mayor que los números originales?

No necesariamente. El MCM de dos números puede ser igual a uno de ellos si uno de los números es un múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.

¿Cómo se calcula el MCM de más de dos números?

Para calcular el MCM de más de dos números, puedes encontrar el MCM de los primeros dos números y luego usar ese resultado para calcular el MCM con el siguiente número, y así sucesivamente.

¿El MCM puede ser un número decimal?

No, el MCM siempre es un número entero. Se trata de múltiplos, y los múltiplos de los números son siempre enteros.

¿Es lo mismo el MCM que el MCD?

No, el MCM (mínimo común múltiplo) y el MCD (máximo común divisor) son conceptos diferentes. El MCM es el múltiplo más pequeño que comparten los números, mientras que el MCD es el número más grande que puede dividir ambos números sin dejar residuo.

Espero que este artículo te haya ayudado a entender cómo calcular el mínimo común múltiplo de 3 y 4 de manera sencilla. ¡Ahora tienes herramientas para resolver problemas de MCM con confianza! No dudes en practicar con otros números y aplicar lo que has aprendido en situaciones cotidianas. ¡La matemática puede ser divertida y útil!