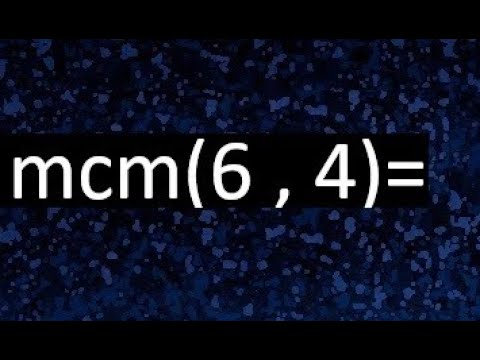¿Alguna vez te has encontrado con el desafío de calcular el mínimo común múltiplo (MCM) de dos números? No te preocupes, ¡estás en el lugar correcto! Hoy vamos a desglosar cómo encontrar el MCM de 6 y 4 de una manera sencilla y paso a paso. El MCM es un concepto fundamental en matemáticas, especialmente cuando se trata de fracciones, divisiones y problemas de sincronización. Así que, ¡vamos a sumergirnos!
¿Qué es el Mínimo Común Múltiplo?
Antes de comenzar con el cálculo, es importante entender qué es el MCM. El Mínimo Común Múltiplo de dos o más números es el múltiplo más pequeño que es común a todos ellos. Piensa en él como el primer tren que sale de la estación y llega a todas las paradas que esos números representan. Si tienes dos trenes (en este caso, los números 6 y 4), el MCM es el primer punto donde ambos trenes se encuentran nuevamente. ¡Vamos a ver cómo se hace esto!
Método 1: Usando la Descomposición en Factores Primos
Una de las maneras más efectivas de calcular el MCM es mediante la descomposición en factores primos. Este método puede parecer un poco complicado al principio, pero una vez que le agarras el truco, ¡es pan comido! Empecemos.
Paso 1: Descomponer cada número en sus factores primos
Para el número 6, sus factores primos son:
- 6 = 2 × 3
Y para el número 4, los factores primos son:
- 4 = 2 × 2 (o 2²)
Paso 2: Identificar todos los factores primos
Ahora que tenemos las descomposiciones, el siguiente paso es identificar todos los factores primos que aparecen en ambos números. Aquí, los factores primos son 2 y 3. Pero, ¿cuántas veces necesitamos cada uno de ellos? Aquí es donde entra el juego de los exponentes.
Paso 3: Elegir el mayor exponente
Para cada factor primo, seleccionamos el mayor exponente que aparece en las descomposiciones:
- Para el 2, el mayor exponente es 2 (de 4).
- Para el 3, el mayor exponente es 1 (de 6).
Paso 4: Multiplicar los factores primos seleccionados
Ahora, multiplicamos estos factores primos con sus mayores exponentes:
- MCM = 2² × 3¹ = 4 × 3 = 12
¡Y ahí lo tienes! El Mínimo Común Múltiplo de 6 y 4 es 12. Pero espera, hay más maneras de llegar a este mismo resultado. ¿Quieres conocer otro método? ¡Vamos a ello!
Método 2: Usando la Regla de los Múltiplos
Este método es más visual y puede ser más fácil de seguir para algunos. Aquí, simplemente enumeramos los múltiplos de cada número hasta encontrar el primero que se repita. ¡Vamos a intentarlo!
Paso 1: Enumerar los múltiplos de cada número
Para el número 6, los primeros múltiplos son:
- 6, 12, 18, 24, 30, …
Y para el número 4, los múltiplos son:
- 4, 8, 12, 16, 20, …
Paso 2: Encontrar el múltiplo común más pequeño
Ahora, simplemente buscamos el primer número que aparece en ambas listas. Si observas, el primer múltiplo común es 12. ¡Así que también llegamos a la misma conclusión!
Método 3: Usando la Relación entre MCM y MCD
Hay una relación interesante entre el Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) que puede ser útil. La fórmula es:
- MCM(a, b) = (a × b) / MCD(a, b)
Paso 1: Calcular el MCD de 6 y 4
Primero, necesitamos encontrar el MCD de 6 y 4. Para ello, podemos utilizar el método de descomposición en factores primos o simplemente listar los divisores de cada número:
- Divisores de 6: 1, 2, 3, 6
- Divisores de 4: 1, 2, 4
El mayor divisor común es 2, así que:
- MCD(6, 4) = 2
Paso 2: Aplicar la fórmula del MCM
Ahora, usando la fórmula:
- MCM(6, 4) = (6 × 4) / 2 = 24 / 2 = 12
Y voilà, llegamos al mismo resultado una vez más. ¡El MCM es 12!
Aplicaciones del Mínimo Común Múltiplo
Ahora que sabes cómo calcular el Mínimo Común Múltiplo de 6 y 4, te preguntarás: «¿Para qué sirve todo esto?» Bueno, el MCM tiene varias aplicaciones prácticas en la vida cotidiana. Aquí te dejo algunas:
Fracciones
Cuando necesitas sumar o restar fracciones, es esencial encontrar un denominador común. El MCM de los denominadores es lo que buscas. Esto facilita el proceso de suma o resta y te permite obtener una respuesta correcta.
Sincronización de Eventos
Imagina que tienes dos alarmas: una que suena cada 6 minutos y otra que suena cada 4 minutos. Si quieres saber cada cuántos minutos ambas alarmas sonarán al mismo tiempo, el MCM te da la respuesta. En este caso, ¡sonarán juntas cada 12 minutos!
Resolución de Problemas Matemáticos
El MCM también es útil en la resolución de problemas más complejos que involucran múltiplos y divisores. Si te enfrentas a un problema que requiere encontrar un número que sea múltiplo de varios números a la vez, el MCM es tu mejor amigo.
Calcular el Mínimo Común Múltiplo de 6 y 4 no es tan complicado como parece. Con los métodos que hemos discutido, puedes hacerlo de varias maneras y elegir la que mejor se adapte a ti. Recuerda que el MCM es una herramienta útil en matemáticas y en la vida cotidiana. ¡No dudes en practicar con otros números y convertirte en un experto en MCM!
¿El MCM siempre es mayor que los números originales?
No necesariamente. El MCM puede ser igual a uno de los números originales si uno de ellos es un múltiplo del otro. Por ejemplo, el MCM de 4 y 8 es 8.
¿Puedo usar el MCM para más de dos números?
¡Claro! El MCM se puede calcular para cualquier cantidad de números. Simplemente descompón cada número en factores primos o usa el método de múltiplos hasta que encuentres el menor múltiplo común.
¿Cuál es la diferencia entre MCM y MCD?
El MCM es el múltiplo más pequeño que es común a todos los números, mientras que el MCD es el mayor divisor que comparten. Ambos son útiles en diferentes contextos matemáticos.
¿Existen calculadoras para encontrar el MCM?
Sí, hay muchas calculadoras en línea que pueden ayudarte a encontrar el MCM de varios números rápidamente. Sin embargo, es bueno entender cómo se calcula manualmente para fortalecer tus habilidades matemáticas.
¿Es importante aprender sobre MCM en la escuela?
Definitivamente. Aprender sobre el MCM y el MCD te ayuda a desarrollar habilidades matemáticas fundamentales que son esenciales para resolver problemas más complejos en el futuro.