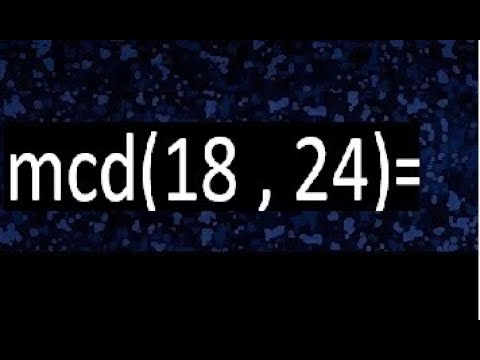Cuando hablamos de números y matemáticas, a veces nos encontramos con términos que pueden parecer un poco intimidantes. Pero no te preocupes, hoy vamos a desglosar uno de esos términos: el Mínimo Común Divisor (MCD). ¿Te has preguntado alguna vez cómo se calcula el MCD de dos números? Si alguna vez te has encontrado con los números 18 y 24 y te has preguntado cómo determinar su MCD, has llegado al lugar indicado. Vamos a sumergirnos en este fascinante mundo matemático, donde desmitificaremos el proceso y aprenderemos a hacerlo paso a paso. Al final, no solo entenderás cómo calcular el MCD, sino que también podrás aplicar este conocimiento a otros números. ¡Así que empecemos!
¿Qué es el Mínimo Común Divisor?
El Mínimo Común Divisor es el número más pequeño que es divisible por dos o más números. Imagina que tienes un grupo de amigos y quieres repartir dulces de manera equitativa. El MCD te dirá cuántos dulces puedes dar a cada amigo sin que sobre ninguno. En el caso de 18 y 24, el MCD te ayudará a determinar la cantidad máxima de dulces que puedes repartir equitativamente entre ellos. Así que, en lugar de quedarte con un montón de sobras, vamos a descubrir cómo calcularlo.
Método 1: Factorización Prima
La factorización prima es una de las maneras más efectivas de encontrar el MCD. ¿Te acuerdas de esos números que solo son divisibles por sí mismos y por 1? Esos son los números primos, y usarlos es como tener una caja de herramientas en la que solo están las herramientas más esenciales. Vamos a desglosar este método.
Paso 1: Factoriza los números
Primero, necesitamos descomponer 18 y 24 en sus factores primos. ¿Listo? Empezamos con 18:
- 18 se puede dividir por 2, lo que nos da 9.
- 9, a su vez, se puede dividir por 3, lo que nos da 3.
- Finalmente, 3 es un número primo.
Así que la factorización prima de 18 es: 2 × 3 × 3 o 2 × 3².
Ahora, vamos con 24:
- 24 se puede dividir por 2, lo que nos da 12.
- 12 se puede dividir por 2 de nuevo, lo que nos da 6.
- 6 se puede dividir por 2 una vez más, lo que nos da 3.
- Finalmente, 3 es un número primo.
Así que la factorización prima de 24 es: 2 × 2 × 2 × 3 o 2³ × 3.
Paso 2: Identifica los factores comunes
Ahora que tenemos las factorizaciones, es momento de identificar los factores comunes. Observando:
- Para 18: 2 × 3²
- Para 24: 2³ × 3
Los factores primos comunes son 2 y 3. Ahora, tomamos el menor exponente de cada factor primo:
- Para 2: el menor exponente es 1 (de 18).
- Para 3: el menor exponente es 1 (de 24).
Paso 3: Multiplica los factores comunes
Ahora, multiplicamos esos factores comunes:
MCD = 2¹ × 3¹ = 2 × 3 = 6.
Así que, ¡ahí lo tienes! El Mínimo Común Divisor de 18 y 24 es 6. ¿No es genial? Ahora puedes usar este método con otros números.
Método 2: Algoritmo de Euclides
Si la factorización prima no es lo tuyo, no te preocupes. Hay otro método que es igual de efectivo y un poco más rápido: el algoritmo de Euclides. Este método es como un atajo en un juego, te lleva al objetivo más rápido. Vamos a ver cómo funciona.
Paso 1: Aplica el algoritmo
Para usar el algoritmo de Euclides, tomamos los dos números y realizamos una serie de divisiones. Empezamos con 24 y 18. Dividimos el número mayor entre el menor:
- 24 ÷ 18 = 1 con un residuo de 6.
Ahora tomamos el divisor anterior (18) y lo dividimos por el residuo (6):
- 18 ÷ 6 = 3 con un residuo de 0.
Cuando llegamos a un residuo de 0, el último divisor es el MCD. En este caso, el MCD es 6. ¡Sorpresa! El resultado es el mismo que antes.
Aplicaciones del Mínimo Común Divisor
Ahora que sabes cómo calcular el MCD, ¿te has preguntado para qué sirve? El MCD tiene varias aplicaciones prácticas en la vida diaria. Por ejemplo, si estás organizando una fiesta y quieres hacer porciones de pastel para tus amigos, el MCD te ayudará a determinar cuántas porciones puedes hacer sin que sobre nada. También es útil en la simplificación de fracciones. Si tienes 18/24, puedes simplificar la fracción dividiendo tanto el numerador como el denominador por su MCD, que es 6. Así que 18/24 se convierte en 3/4. ¡Así de fácil!
Ejercicios Prácticos
Ahora que tienes el conocimiento teórico, ¿por qué no lo pones en práctica? Aquí hay algunos ejercicios para que te diviertas:
- Calcula el MCD de 30 y 45.
- Calcula el MCD de 50 y 75.
- Calcula el MCD de 36 y 60.
Recuerda usar ambos métodos y ver cuál prefieres. ¡La práctica hace al maestro!
En resumen, calcular el Mínimo Común Divisor de dos números no tiene por qué ser un proceso complicado. Ya sea que elijas la factorización prima o el algoritmo de Euclides, lo importante es entender los pasos y practicar. Con el tiempo, te sentirás más cómodo con estos cálculos y podrás aplicarlos en situaciones cotidianas. Así que la próxima vez que te enfrentes a un par de números, ya sabes qué hacer. ¡No hay excusa para no ser un experto en MCD!
¿El MCD siempre será menor que los números originales?
Sí, el MCD de dos números siempre será menor o igual que el número más pequeño de los dos. Esto se debe a que el MCD es un divisor de ambos números.
¿Puedo calcular el MCD de más de dos números?
¡Por supuesto! Puedes calcular el MCD de tres o más números. Simplemente calcula el MCD de los dos primeros números y luego utiliza ese resultado para calcular el MCD con el siguiente número, y así sucesivamente.
¿El MCD de dos números primos siempre será 1?
Exactamente. Si ambos números son primos y no tienen factores en común, su MCD será 1, lo que significa que son coprimos.
¿Es útil el MCD en la programación?
Sí, el MCD es muy útil en programación, especialmente en algoritmos relacionados con la teoría de números y la criptografía. Los programadores a menudo utilizan el MCD para simplificar fracciones y resolver problemas relacionados con divisibilidad.
¿Puedo usar el MCD para simplificar expresiones algebraicas?
Sí, el MCD puede ser utilizado para simplificar expresiones algebraicas, similar a cómo se simplifican fracciones. Esto puede ser muy útil en matemáticas avanzadas.