Entendiendo los Fundamentos de Máximos y Mínimos
¿Alguna vez te has preguntado cómo se determina el punto más alto o más bajo de una función? Este concepto es fundamental en matemáticas y tiene aplicaciones en diversas áreas como la economía, la ingeniería y las ciencias sociales. En este artículo, vamos a desglosar qué son los máximos y mínimos relativos y absolutos, cómo identificarlos y por qué son importantes. Te prometo que al final de esta lectura, tendrás una comprensión clara y práctica de estos conceptos, ¡así que empecemos!
### ¿Qué son los Máximos y Mínimos?
Antes de entrar en detalles técnicos, vamos a aclarar qué significan estos términos. Los máximos son los puntos en los que una función alcanza su valor más alto en un intervalo determinado, mientras que los mínimos son donde alcanza su valor más bajo. Imagínate que estás escalando una montaña: el punto más alto que alcanzas es un máximo, y el punto más bajo del valle que cruzas es un mínimo. Ahora bien, dentro de estos conceptos, hay dos categorías: máximos y mínimos relativos, y máximos y mínimos absolutos.
### Máximos y Mínimos Relativos vs. Absolutos
Para no perderte en la terminología, vamos a desglosar estas categorías.
#### Máximos y Mínimos Relativos
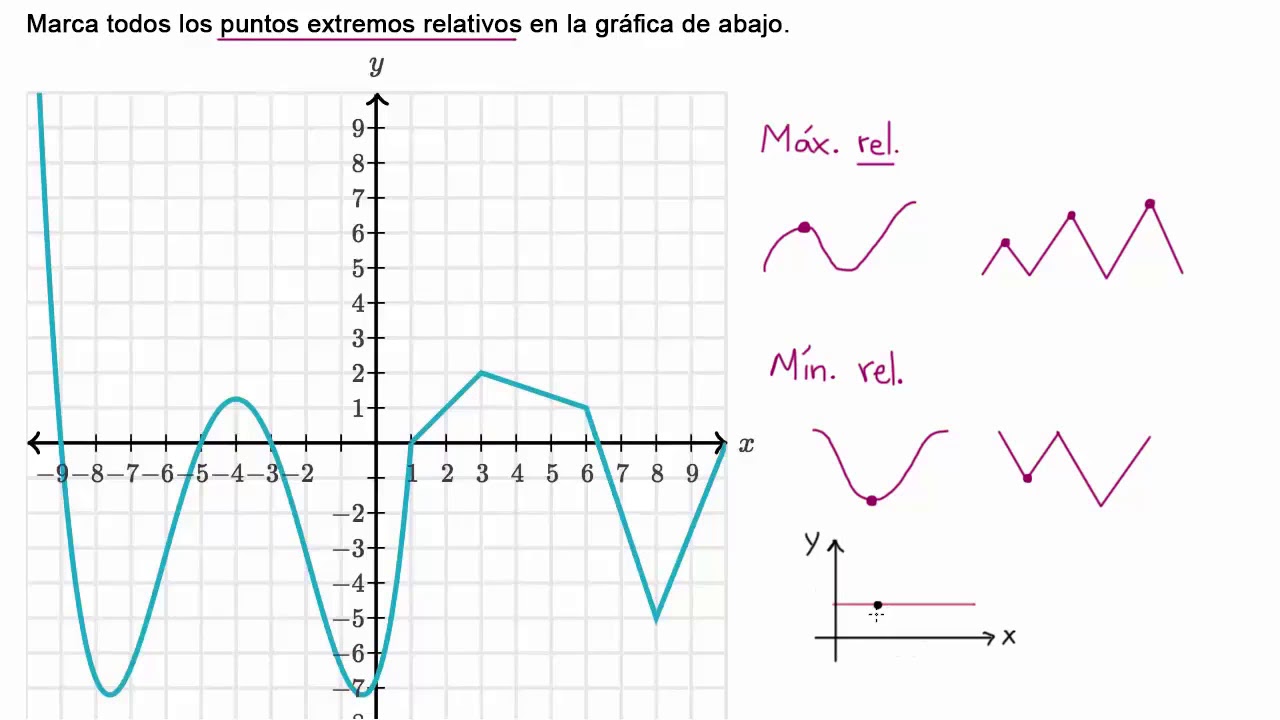
Los máximos y mínimos relativos son aquellos que son más altos o más bajos que sus puntos vecinos. Por ejemplo, si estás en una colina, el pico que alcanzas puede ser el más alto de esa área, pero no necesariamente el más alto de toda la región. Esto significa que hay otros picos en otras áreas que podrían ser más altos. En términos matemáticos, un máximo relativo es un punto donde la función cambia de creciente a decreciente, y un mínimo relativo es donde cambia de decreciente a creciente.
#### Máximos y Mínimos Absolutos
Por otro lado, los máximos y mínimos absolutos son los más altos y más bajos de toda la función en un intervalo dado. Siguiendo con nuestra analogía de la montaña, el máximo absoluto sería el pico más alto de todas las montañas en un país, mientras que el mínimo absoluto sería el punto más bajo, como el nivel del mar. En resumen, un máximo absoluto es el valor más grande que toma la función en todo su dominio, mientras que un mínimo absoluto es el más pequeño.
### Cómo Identificar Máximos y Mínimos
Ahora que tenemos claro qué son los máximos y mínimos, veamos cómo podemos identificarlos en una función. Hay varias técnicas que podemos utilizar, y aquí te las explico de manera sencilla.
#### Derivadas
Una de las herramientas más poderosas en cálculo es la derivada. La derivada de una función nos indica la pendiente de la misma en un punto dado. Si la derivada es cero en un punto, eso puede ser un indicativo de un máximo o mínimo. Aquí hay un paso a paso para usar derivadas:
1. Encuentra la derivada de la función. Esto te dará la tasa de cambio de la función.
2. Iguala la derivada a cero. Esto te ayudará a encontrar los puntos críticos, donde la función puede tener un máximo o mínimo.
3. Usa la prueba de la segunda derivada. Si la segunda derivada es positiva, tienes un mínimo; si es negativa, tienes un máximo.
#### Análisis Gráfico
A veces, simplemente graficar la función puede ayudarte a visualizar los máximos y mínimos. Puedes usar herramientas gráficas como Desmos o GeoGebra para trazar la función y observar los puntos donde se alcanzan los picos y valles. Esto puede ser especialmente útil si no estás cómodo trabajando con derivadas.
### Ejemplos Prácticos
Ahora que sabemos cómo identificar estos puntos, veamos algunos ejemplos prácticos para consolidar nuestro aprendizaje.
#### Ejemplo 1: Función Cuadrática
Consideremos la función ( f(x) = -x^2 + 4x ).
1. Derivada: La derivada es ( f'(x) = -2x + 4 ).
2. Igualar a cero: ( -2x + 4 = 0 ) nos da ( x = 2 ).
3. Segunda derivada: ( f»(x) = -2 ), que es negativa, por lo que ( x = 2 ) es un máximo relativo.
Ahora, evaluamos ( f(2) = -2^2 + 4(2) = 4 ). Así que el máximo relativo es ( (2, 4) ).
#### Ejemplo 2: Función Trigonométrica
Consideremos la función ( g(x) = sin(x) ).
1. Derivada: La derivada es ( g'(x) = cos(x) ).
2. Igualar a cero: Esto ocurre en ( x = frac{pi}{2} + kpi ) donde ( k ) es un entero.
3. Máximos y Mínimos: En el intervalo ( [0, 2pi] ), tenemos un máximo absoluto en ( x = frac{pi}{2} ) y un mínimo absoluto en ( x = frac{3pi}{2} ).
### Aplicaciones de Máximos y Mínimos
Los conceptos de máximos y mínimos no son solo ejercicios académicos. Tienen aplicaciones prácticas en la vida real. Por ejemplo, en la economía, se utilizan para maximizar ganancias y minimizar costos. En la ingeniería, se aplican para optimizar el diseño de estructuras. Y en la biología, se pueden usar para entender el crecimiento de poblaciones.
### Consejos para Estudiar Máximos y Mínimos
Si estás aprendiendo sobre estos conceptos, aquí tienes algunos consejos:
1. Practica con ejemplos. Cuanto más practiques, más cómodo te sentirás con el material.
2. Usa recursos visuales. Las gráficas pueden hacer que los conceptos sean más fáciles de entender.
3. No dudes en preguntar. Si algo no te queda claro, busca ayuda de un profesor o tutor.
### Preguntas Frecuentes
1. ¿Cuál es la diferencia entre un máximo y un mínimo absoluto?
La diferencia radica en el rango: el máximo absoluto es el valor más alto en todo el dominio de la función, mientras que el máximo relativo es solo el más alto en un intervalo específico.
2. ¿Cómo sé si tengo un máximo o mínimo?
Puedes usar la prueba de la primera o segunda derivada para determinar la naturaleza del punto crítico.
3. ¿Puedo tener más de un máximo o mínimo en una función?
Sí, una función puede tener múltiples máximos y mínimos, tanto relativos como absolutos.
4. ¿Por qué son importantes los máximos y mínimos en la vida real?
Son cruciales para la optimización en diversas disciplinas, como economía, ingeniería y ciencias, ayudando a tomar decisiones informadas.
5. ¿Existen funciones que no tienen máximos o mínimos?
Sí, algunas funciones, como las que son estrictamente crecientes o decrecientes, no tienen máximos o mínimos en su dominio.
### Conclusión
Ahora que hemos explorado a fondo los conceptos de máximos y mínimos relativos y absolutos, y cómo identificarlos, estás mejor equipado para aplicar estos conocimientos en situaciones prácticas. Recuerda que la clave está en practicar y familiarizarte con las herramientas matemáticas que te ayudarán a encontrar estos puntos críticos. ¡Buena suerte en tu viaje matemático!