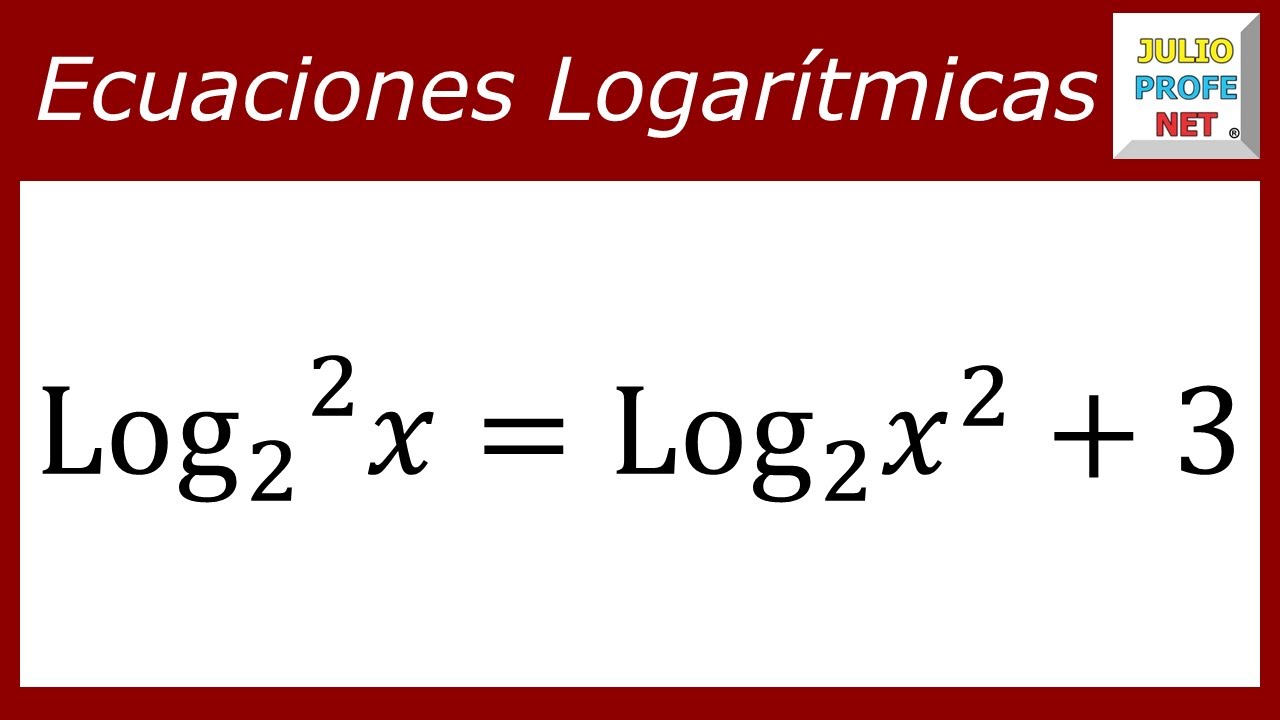¿Te has encontrado alguna vez con el término «logaritmos al cuadrado» y te has preguntado qué demonios significa? No estás solo. Este concepto puede parecer complicado al principio, pero con un poco de práctica y comprensión, se convierte en algo bastante manejable. Los logaritmos son herramientas matemáticas poderosas que nos ayudan a resolver ecuaciones exponenciales de una manera más sencilla. Imagina que los logaritmos son como una linterna en la oscuridad de las matemáticas: iluminan el camino y te ayudan a entender lo que de otro modo podría ser confuso.
Ahora, ¿qué pasa cuando hablamos de logaritmos al cuadrado? Aquí es donde la cosa se pone interesante. Este concepto combina la idea de los logaritmos con la operación de elevar al cuadrado. Si bien puede parecer un poco intimidante al principio, en este artículo desglosaremos todo lo que necesitas saber, paso a paso. Desde los fundamentos hasta ejemplos prácticos, te guiaré en este viaje matemático. Así que, ¡vamos a sumergirnos!
¿Qué Son los Logaritmos?
Antes de entrar en el tema de los logaritmos al cuadrado, es esencial tener una comprensión básica de lo que son los logaritmos. En términos simples, un logaritmo responde a la pregunta: ¿a qué potencia debo elevar un número base para obtener otro número? Por ejemplo, si tienes el logaritmo en base 10 de 100, la respuesta es 2, porque 10 elevado a la potencia de 2 es igual a 100.
Los logaritmos tienen varias bases, pero las más comunes son la base 10 (logaritmos comunes) y la base e (logaritmos naturales). La notación de un logaritmo se representa como log_b(a), donde «b» es la base y «a» es el número del que deseas calcular el logaritmo. Así que, si alguna vez te sientes perdido en un mar de números, recuerda que los logaritmos son tu amigo.
Logaritmos al Cuadrado: ¿Qué Significan?
Ahora que tenemos una idea de lo que son los logaritmos, ¿qué significa realmente «logaritmos al cuadrado»? Cuando hablamos de logaritmos al cuadrado, nos referimos a tomar el logaritmo de un número y luego elevar ese resultado al cuadrado. Por ejemplo, si calculas log(10) y luego lo elevas al cuadrado, obtienes (log(10))^2.
Pero, ¿por qué querrías hacer esto? Bueno, hay situaciones en matemáticas y ciencias donde trabajar con logaritmos al cuadrado puede simplificar cálculos o hacer que ciertos patrones sean más evidentes. Por ejemplo, en estadística y en análisis de datos, los logaritmos al cuadrado pueden ayudar a normalizar datos que tienen una distribución sesgada.
Propiedades de los Logaritmos
Para comprender mejor los logaritmos al cuadrado, es crucial conocer algunas propiedades de los logaritmos. Aquí hay un resumen rápido:
1. Logaritmo de un Producto: log_b(x * y) = log_b(x) + log_b(y)
2. Logaritmo de un Cociente: log_b(x / y) = log_b(x) – log_b(y)
3. Logaritmo de una Potencia: log_b(x^n) = n * log_b(x)
Estas propiedades son útiles porque te permiten manipular logaritmos de manera que simplifiquen los cálculos. Por ejemplo, si tienes que calcular log(1000) y sabes que 1000 es 10^3, puedes usar la propiedad de la potencia para obtener log(1000) = 3 * log(10).
Ejemplos Prácticos de Logaritmos al Cuadrado
Para que todo esto tenga sentido, veamos algunos ejemplos prácticos. Supongamos que queremos calcular el logaritmo en base 10 de 100 y luego elevarlo al cuadrado.
1. Paso 1: Calcular log(100)
– Sabemos que log(100) = 2, porque 10^2 = 100.
2. Paso 2: Elevar al cuadrado
– Entonces, (log(100))^2 = 2^2 = 4.
¡Y ahí lo tienes! Un cálculo sencillo que ilustra cómo funcionan los logaritmos al cuadrado.
Más Ejemplos con Diferentes Bases
Vamos a complicar un poco las cosas y usar otra base, digamos la base 2. Imagina que quieres calcular log_2(8) y luego elevarlo al cuadrado.
1. Paso 1: Calcular log_2(8)
– Sabemos que 2^3 = 8, así que log_2(8) = 3.
2. Paso 2: Elevar al cuadrado
– (log_2(8))^2 = 3^2 = 9.
Como ves, el proceso es el mismo sin importar la base. ¡Solo tienes que aplicar las propiedades y seguir adelante!
Aplicaciones de los Logaritmos al Cuadrado
Los logaritmos al cuadrado tienen varias aplicaciones prácticas en diferentes campos. Desde la biología hasta la ingeniería, su utilidad es bastante amplia. Aquí hay algunas áreas donde se utilizan:
Estadística
En estadística, a menudo lidiamos con datos que no se distribuyen de manera uniforme. Utilizar logaritmos al cuadrado puede ayudar a normalizar estos datos, haciéndolos más fáciles de analizar. Por ejemplo, si estás trabajando con datos de ingresos, que a menudo tienen una distribución sesgada, aplicar logaritmos al cuadrado puede ayudar a suavizar esa distribución.
Ciencias de Datos
En el análisis de datos, los logaritmos al cuadrado pueden ser útiles para transformar variables y hacer que las relaciones entre ellas sean más evidentes. Esto es especialmente importante en modelos de regresión, donde se busca establecer relaciones entre variables.
Física y Química
En ciencias físicas y químicas, los logaritmos al cuadrado pueden aparecer en fórmulas que describen reacciones y procesos. Por ejemplo, en la ley de decaimiento radiactivo, los logaritmos pueden ayudar a calcular la cantidad de material que queda después de un cierto tiempo.
Desmitificando los Logaritmos al Cuadrado
Así que, ahora que hemos explorado los logaritmos al cuadrado, ¿te sientes más cómodo con el tema? La clave está en practicar y aplicar estos conceptos a problemas reales. No te desanimes si al principio parece un poco complicado. Con el tiempo y la práctica, se volverá más natural.
Recuerda, cada vez que te encuentres con un logaritmo al cuadrado, piensa en las propiedades y en cómo puedes descomponer el problema en pasos más pequeños. ¡Es como resolver un rompecabezas!
¿Cuál es la diferencia entre logaritmos y logaritmos al cuadrado?
Los logaritmos son funciones que responden a la pregunta de a qué potencia se debe elevar una base para obtener un número. Los logaritmos al cuadrado, en cambio, son el resultado de tomar un logaritmo y elevarlo al cuadrado.
¿Dónde se utilizan los logaritmos al cuadrado en la vida real?
Se utilizan en diversas áreas como estadística, ciencias de datos, física y química para simplificar cálculos y analizar datos que no siguen una distribución normal.
¿Cómo puedo practicar logaritmos al cuadrado?
Una buena forma de practicar es resolver problemas de matemáticas que involucren logaritmos y experimentar con diferentes bases. También puedes utilizar herramientas en línea o aplicaciones educativas para practicar.
¿Son los logaritmos al cuadrado más complicados que los logaritmos simples?
No necesariamente. Aunque puede parecer más complicado al principio, una vez que entiendes los conceptos básicos de los logaritmos, elevarlos al cuadrado es simplemente una cuestión de seguir pasos adicionales.
¿Puedo usar logaritmos al cuadrado en calculadoras comunes?
Sí, la mayoría de las calculadoras científicas tienen funciones para calcular logaritmos. Solo asegúrate de calcular primero el logaritmo y luego elevar el resultado al cuadrado.
En conclusión, los logaritmos al cuadrado son un concepto que, aunque puede parecer complicado al principio, se vuelve más accesible con la práctica y la comprensión adecuada. Así que la próxima vez que te enfrentes a ellos, recuerda: ¡tienes las herramientas para dominarlos!