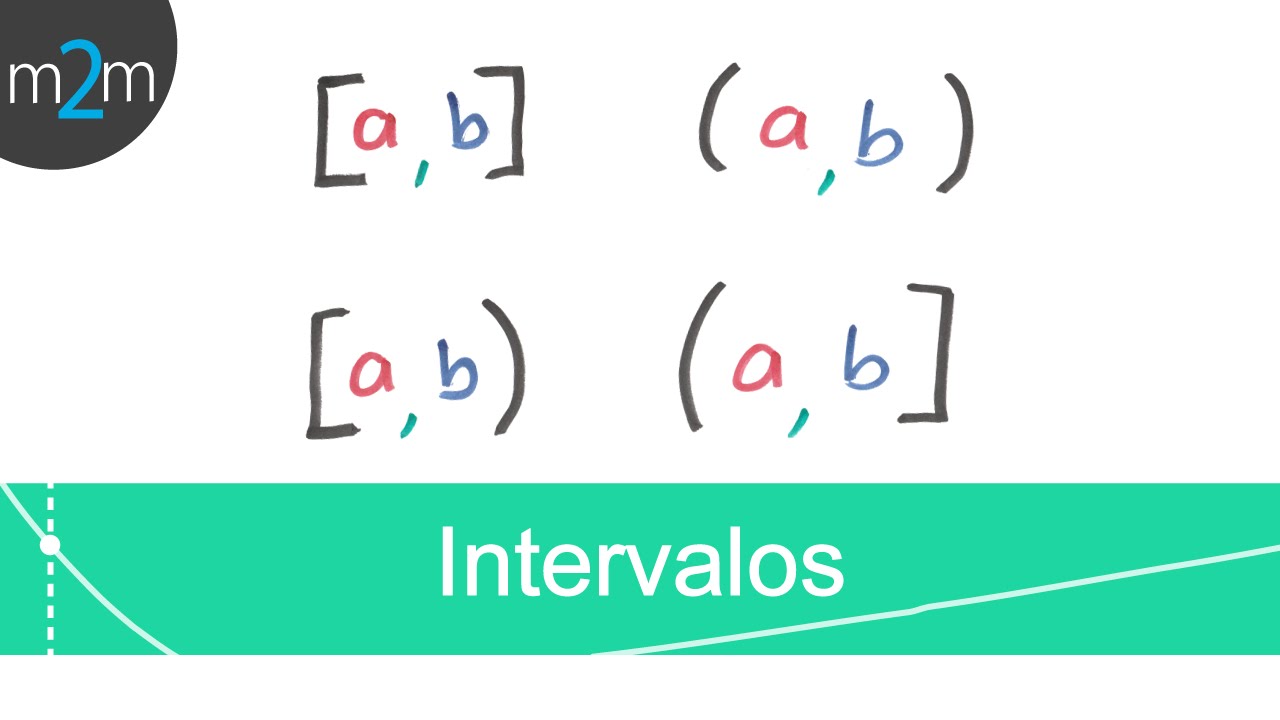
Si alguna vez te has topado con una clase de matemáticas o has leído sobre análisis matemático, es probable que hayas escuchado los términos «intervalos cerrados» y «abiertos». Pero, ¿qué significan realmente? Y más importante aún, ¿por qué deberían importarte? Imagina que estás en un parque, y hay un camino que va de un extremo a otro. Un intervalo cerrado sería como un camino que tiene barreras en ambos extremos, mientras que un intervalo abierto sería como un camino que no tiene barreras. Este simple ejemplo nos ayuda a visualizar la diferencia fundamental entre ambos conceptos. A lo largo de este artículo, vamos a desglosar estos intervalos, dándote ejemplos claros y prácticos, para que al final puedas entenderlos a la perfección.
¿Qué son los Intervalos Cerrados?
Comencemos con los intervalos cerrados. En términos matemáticos, un intervalo cerrado se denota como [a, b], donde «a» y «b» son los extremos del intervalo. La clave aquí es que incluye ambos extremos. Así que si tienes un intervalo como [2, 5], esto significa que todos los números entre 2 y 5 están incluidos, y también los propios 2 y 5. Es como si estuvieras invitando a todos tus amigos a una fiesta, incluyendo a aquellos que llegan justo a la hora, y también a los que llegan un poco más tarde. ¿Te imaginas qué pasaría si no los invitaras? ¡Podrías perderte de grandes momentos!
Ejemplos Prácticos de Intervalos Cerrados
Veamos algunos ejemplos prácticos para hacer esto más claro. Supongamos que estás midiendo la temperatura en una habitación. Si la temperatura se mantiene entre [18°C, 22°C], esto significa que la temperatura puede ser 18°C, 22°C, o cualquier valor en el medio, como 19°C, 20°C o 21°C. ¿Ves cómo abarca todo ese rango? Otro ejemplo podría ser en un examen, donde un estudiante necesita obtener una calificación entre [60, 100] para aprobar. En este caso, cualquier puntuación dentro de ese rango, incluyendo los límites, significa éxito.
¿Qué son los Intervalos Abiertos?
Ahora, pasemos a los intervalos abiertos. Un intervalo abierto se denota como (a, b), lo que significa que incluye todos los números entre «a» y «b», pero no incluye los extremos. Así que, si tienes un intervalo como (2, 5), esto significa que puedes tener 2.1, 3, 4.9, pero no puedes incluir 2 ni 5. Es como si tuvieras una fiesta, pero decidieras que solo puedes entrar si llegas un poco después de que comience. Si llegas justo a la hora, ¡te quedas afuera!
Ejemplos Prácticos de Intervalos Abiertos
Siguiendo con la idea de la temperatura, si decimos que la temperatura debe estar en el intervalo (18°C, 22°C), esto significa que la temperatura no puede ser exactamente 18°C o 22°C, sino que debe estar entre esos dos valores. Otro ejemplo sería en el caso de un juego de apuestas, donde un jugador solo puede ganar si su puntuación está entre (50, 100). Aquí, una puntuación de 50 o 100 no contaría, solo las que estén entre esos límites.
¿Por qué son Importantes los Intervalos Cerrados y Abiertos?
Entonces, ¿por qué deberías preocuparte por estos intervalos? La respuesta es simple: son fundamentales en muchas áreas de la matemática y la ciencia. Desde la estadística hasta el cálculo, los intervalos te ayudan a definir rangos, establecer límites y tomar decisiones basadas en datos. Imagina que estás tratando de analizar el rendimiento de tus inversiones. Al usar intervalos, puedes determinar rápidamente qué inversiones están dentro de un rango aceptable y cuáles no. Es como tener un mapa que te guía en un viaje complicado.
La Diferencia entre Intervalos Cerrados y Abiertos
Si bien ya hemos mencionado las diferencias, es importante subrayarlas. La inclusión o exclusión de los extremos es lo que realmente define si un intervalo es abierto o cerrado. Un intervalo cerrado incluye sus límites, mientras que un intervalo abierto los deja fuera. Esto puede parecer un detalle menor, pero en matemáticas, los pequeños detalles pueden marcar una gran diferencia. Piensa en ello como en una carrera. Si la línea de meta está incluida, todos los que cruzan la línea ganan. Pero si no está incluida, solo los que cruzan antes de la línea pueden ser considerados ganadores. ¡Todo un dilema!
Aplicaciones en la Vida Real
Los intervalos no solo son un concepto académico; tienen aplicaciones prácticas en la vida diaria. Por ejemplo, en la programación de computadoras, los intervalos se utilizan para definir rangos de valores que una variable puede tomar. En economía, se utilizan para establecer márgenes de precios. Y en ciencias, son esenciales para definir intervalos de confianza en experimentos. ¿Te has dado cuenta de que los intervalos están en todas partes? Desde la música, donde las notas pueden ser consideradas en intervalos, hasta la física, donde las medidas pueden tener rangos específicos. ¡Es un concepto universal!
Ejemplos Combinados de Intervalos
Para hacer las cosas aún más interesantes, ¿qué tal si combinamos intervalos abiertos y cerrados? A veces, los problemas requieren que uses ambos tipos. Por ejemplo, en un examen, podrías tener que definir un rango de calificaciones donde [60, 70) significa que 60 está incluido, pero 70 no lo está. Esto podría indicar que un estudiante necesita al menos 60 para pasar, pero no puede obtener exactamente 70. Es una manera de establecer un límite superior que no se puede alcanzar. ¡Interesante, ¿verdad?
Consejos para Identificar Intervalos
Ahora que hemos cubierto bastante sobre intervalos, aquí van algunos consejos para ayudarte a identificar y trabajar con ellos. Primero, siempre presta atención a los símbolos. Un corchete [ o ] indica que el número está incluido, mientras que un paréntesis ( o ) indica que no lo está. Segundo, si estás trabajando con un gráfico, asegúrate de marcar claramente los límites de tu intervalo. Y finalmente, practica. Cuanto más trabajes con intervalos, más fácil te resultará reconocerlos y utilizarlos en diferentes contextos.
¿Puedo tener un intervalo que combine cerrado y abierto?
Sí, puedes tener intervalos que combinan ambos tipos, como [a, b), donde «a» está incluido y «b» no. Esto es útil en muchas aplicaciones matemáticas.
¿Cómo se grafican los intervalos abiertos y cerrados?
En un gráfico, los intervalos cerrados se representan con un punto sólido en los extremos, mientras que los abiertos se representan con un punto vacío.
¿Los intervalos se utilizan en otras disciplinas además de matemáticas?
Absolutamente. Los intervalos se utilizan en estadística, ciencias, economía, y muchas otras disciplinas para definir rangos y establecer límites.
¿Puedo mezclar intervalos en una sola expresión?
Sí, puedes mezclar intervalos en una sola expresión, como en [a, b) ∪ (c, d]. Esto significa que estás combinando diferentes rangos de valores.
¿Cómo puedo practicar el uso de intervalos?
Una buena manera de practicar es resolver problemas matemáticos que involucren intervalos, y también puedes intentar graficar diferentes intervalos para visualizar mejor su uso.
Con esto, esperamos que tengas una comprensión más clara de los intervalos cerrados y abiertos. ¡Ahora es tu turno de ponerlo en práctica!