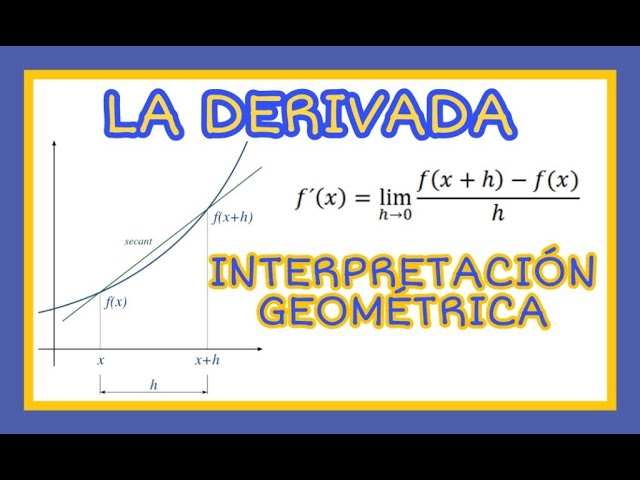
La Esencia de la Derivada en el Cambio
Cuando hablamos de derivadas, muchos se sienten abrumados por la complejidad de las fórmulas y los símbolos. Pero, ¿qué pasaría si te dijera que la derivada es simplemente una forma de entender el cambio? Imagina que estás conduciendo un coche y observas el velocímetro. La velocidad en ese momento es, de hecho, una derivada: te dice cómo cambia tu posición en el tiempo. En matemáticas, la derivada cumple un papel similar, pero en lugar de medir la velocidad, mide cómo cambia una función a medida que cambias su entrada. Este concepto se puede visualizar de manera geométrica, lo que lo hace aún más interesante y accesible.
¿Qué es la Derivada?
En términos simples, la derivada de una función en un punto específico nos dice la pendiente de la tangente a la curva de esa función en ese punto. Piensa en ello como si estuvieras tratando de encontrar la inclinación de una colina en un lugar particular. Si estás en la cima de una montaña, la pendiente puede ser bastante empinada, mientras que en el valle, puede ser casi plana. Así es como funciona la derivada: mide cuán empinada es la curva en un punto dado.
La Tangente y la Curva
Visualiza una curva suave en un gráfico. Ahora, imagina que quieres saber cómo se comporta la curva en un punto específico. Lo que haces es dibujar una línea recta que toque la curva justo en ese punto. Esta línea se llama «línea tangente». La pendiente de esta línea tangente es precisamente la derivada de la función en ese punto. Pero, ¿por qué es tan importante esta línea tangente? Porque nos da una idea clara de cómo se comporta la función en las cercanías de ese punto. Si la pendiente es positiva, la función está aumentando; si es negativa, está disminuyendo. ¡Es como tener un mapa de ruta para entender el comportamiento de las funciones!
La Notación de la Derivada
Ahora que tenemos una idea básica de qué es la derivada, hablemos de cómo se representa. La notación más común es f'(x), donde f representa nuestra función y x es el punto en el que estamos evaluando la derivada. Otra notación popular es dy/dx, que se lee «cambio en y sobre cambio en x». Este último es especialmente útil porque nos recuerda que estamos hablando de tasas de cambio. ¿No es genial cómo un símbolo puede encapsular tanto significado?
La Regla del Límite
Para entender cómo se calcula la derivada, necesitamos hablar sobre los límites. La derivada se define formalmente como el límite de la tasa de cambio promedio a medida que el intervalo de tiempo se aproxima a cero. Suena complicado, pero imagina que estás tratando de medir la velocidad de un coche. Si solo miras la distancia recorrida en un segundo, podrías tener una idea, pero no sería precisa. En cambio, si miras la distancia recorrida en un intervalo de tiempo cada vez más pequeño, eventualmente podrás medir la velocidad en un instante específico. Eso es lo que hace la derivada: afina nuestra medida del cambio hasta el punto más preciso posible.
Interpretación Visual de la Derivada
Volviendo a nuestra analogía de la carretera, si representamos la función como una curva en un gráfico, la derivada nos da la inclinación de esa curva en cada punto. Puedes imaginarlo como una montaña rusa: en algunos puntos, la pista es muy empinada, lo que significa que la derivada es alta. En otros, la pista es casi plana, lo que indica una derivada baja. Si la montaña rusa baja rápidamente, eso significa que la derivada es negativa, y si sube, la derivada es positiva. Así que cada vez que veas una curva, pregúntate: ¿qué tan empinada es aquí?
Aplicaciones de la Derivada en el Mundo Real
Las derivadas no son solo un concepto abstracto; tienen aplicaciones prácticas en la vida cotidiana. Desde la economía hasta la biología, las derivadas nos ayudan a modelar situaciones reales. Por ejemplo, en economía, podemos usar derivadas para maximizar ganancias o minimizar costos. Si una empresa quiere saber cómo cambiará su ingreso si aumenta el precio de un producto, puede usar la derivada para predecir ese cambio. En biología, las derivadas se utilizan para modelar el crecimiento de poblaciones, donde la tasa de crecimiento puede variar con el tiempo.
Tipos de Derivadas
Existen diferentes tipos de derivadas que pueden ser útiles dependiendo del contexto. La derivada ordinaria es la más común, pero también hay derivadas parciales, que se utilizan cuando trabajamos con funciones de múltiples variables. Imagina que estás en una fiesta con amigos, y quieres saber cómo cambia el ambiente a medida que agregas más música o comida. Las derivadas parciales te permiten analizar el efecto de cada uno de esos factores de manera individual. ¡Es como tener un control remoto para ajustar cada variable en una fiesta!
El Teorema de Rolle y el Teorema del Valor Intermedio
Cuando profundizamos en el estudio de las derivadas, encontramos algunos teoremas interesantes. El Teorema de Rolle establece que si una función es continua en un intervalo cerrado y derivable en el intervalo abierto, entonces hay al menos un punto donde la derivada es cero. Esto significa que en algún lugar entre dos extremos, la función debe tener un máximo o mínimo. Por otro lado, el Teorema del Valor Intermedio nos dice que si una función es continua, entonces toma todos los valores entre su mínimo y máximo. Esto es esencial para entender cómo se comportan las funciones y por qué las derivadas son tan importantes.
La Segunda Derivada
Una vez que entiendes la primera derivada, es natural preguntarse: ¿y qué hay de la segunda derivada? La segunda derivada nos dice cómo está cambiando la pendiente de la curva. ¿Recuerdas la montaña rusa? La primera derivada te dice si estás subiendo o bajando, pero la segunda derivada te dice si la montaña rusa se está volviendo más empinada o menos empinada. Si la segunda derivada es positiva, significa que la curva se está volviendo más empinada; si es negativa, se está aplanando. ¡Es como tener un doble control sobre la emoción de la montaña rusa!
Interpretación de la Segunda Derivada
La segunda derivada tiene aplicaciones importantes en el análisis de la concavidad de una función. Si una función es cóncava hacia arriba, su segunda derivada será positiva, lo que indica que la función tiene un mínimo local. Por el contrario, si es cóncava hacia abajo, la segunda derivada será negativa, sugiriendo un máximo local. Esto es esencial para optimizar funciones en diversas disciplinas, desde la ingeniería hasta la economía. ¡Es como tener un mapa del tesoro que te indica dónde están los máximos y mínimos!
En resumen, la interpretación geométrica de la derivada nos ofrece una manera poderosa de entender el cambio en las matemáticas. A través de visualizaciones y aplicaciones prácticas, podemos ver cómo las derivadas no son solo un conjunto de reglas y fórmulas, sino herramientas que nos ayudan a navegar por el mundo que nos rodea. La próxima vez que pienses en derivadas, recuerda la montaña rusa y cómo cada pendiente te cuenta una historia sobre el comportamiento de una función. ¿No es fascinante cómo un concepto matemático puede tener tanto significado y aplicación?
¿Por qué es importante entender la derivada en matemáticas?
La derivada es fundamental porque nos ayuda a comprender cómo cambian las funciones. Desde la velocidad en física hasta el crecimiento en biología, su aplicación es amplia y esencial para muchas disciplinas.
¿Qué diferencia hay entre la derivada y la segunda derivada?
La derivada nos dice la pendiente de una función en un punto específico, mientras que la segunda derivada nos indica cómo cambia esa pendiente. Esto nos ayuda a identificar máximos y mínimos en la función.
¿Cómo se relacionan las derivadas con el mundo real?
Las derivadas se utilizan en muchas áreas, como la economía para optimizar ganancias y en la biología para modelar el crecimiento poblacional. Son herramientas valiosas para analizar cambios en diversas situaciones.
¿Qué es la notación de Leibniz y cómo se utiliza?
La notación de Leibniz, que se expresa como dy/dx, es una forma de representar la derivada que enfatiza el cambio en y con respecto al cambio en x. Es especialmente útil para entender tasas de cambio en problemas aplicados.
¿Cómo puedo practicar el cálculo de derivadas?
Una buena manera de practicar es resolver ejercicios de diferentes funciones y graficar sus derivadas. También puedes utilizar aplicaciones en línea que te permitan visualizar las funciones y sus pendientes.