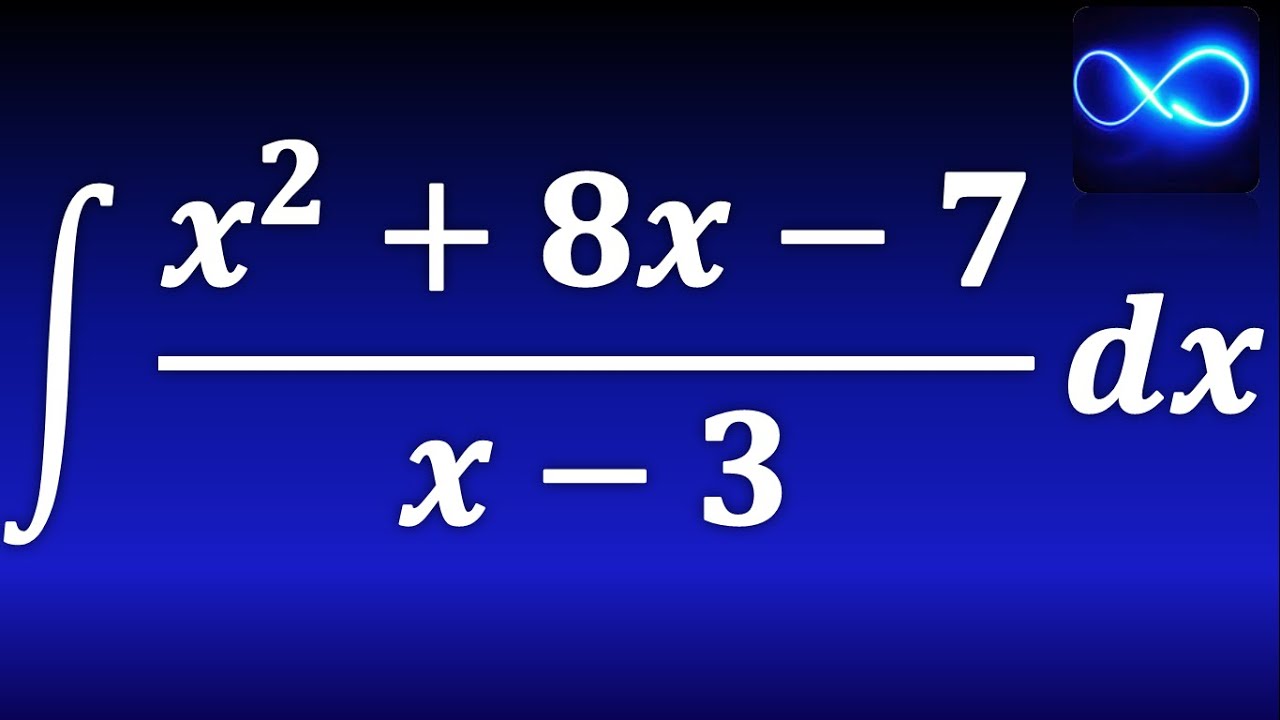¿Alguna vez te has encontrado con un polinomio que parece un rompecabezas? No te preocupes, ¡no estás solo! La integral por división de polinomios es una herramienta poderosa que te ayudará a resolver problemas de integración que, a simple vista, parecen complicados. En este artículo, vamos a desglosar el proceso paso a paso, de manera que puedas dominarlo y aplicarlo con confianza. Prepárate para adentrarte en el mundo de las integrales y descubrir cómo la división de polinomios puede hacer que todo sea mucho más fácil.
La integral de un polinomio no es solo un ejercicio matemático; es como una aventura en la que cada paso te acerca más a la solución. Imagina que estás navegando por un río: a veces hay aguas tranquilas y otras veces hay rápidos. La división de polinomios es como encontrar el camino más suave para avanzar. A lo largo de este artículo, no solo te enseñaré cómo realizar estas integrales, sino que también te proporcionaré ejemplos prácticos que harán que el proceso sea más claro y menos intimidante. Así que, si estás listo, ¡vamos a sumergirnos en el tema!
¿Qué es la División de Polinomios?
La división de polinomios es un proceso que nos permite dividir un polinomio por otro, similar a cómo dividir números enteros. ¿Te suena familiar? Imagina que tienes un pastel (el polinomio) y quieres compartirlo entre varias personas (el divisor). El objetivo es determinar cuánto le toca a cada uno y, a veces, sobran migajas. Esto es exactamente lo que sucede cuando dividimos polinomios.
En términos más formales, si tenemos dos polinomios ( P(x) ) (el numerador) y ( D(x) ) (el denominador), queremos encontrar el cociente ( Q(x) ) y el residuo ( R(x) ) tal que:
[ P(x) = D(x) cdot Q(x) + R(x) ]
donde el grado de ( R(x) ) es menor que el grado de ( D(x) ). Este es el primer paso fundamental que necesitamos entender antes de abordar las integrales.
¿Por qué es Importante la Integral por División de Polinomios?
La integral por división de polinomios es esencial en el cálculo porque simplifica la tarea de integrar funciones que son fracciones de polinomios. Si te enfrentas a una integral como:
[ int frac{P(x)}{D(x)} , dx ]
puede parecer desalentador al principio. Sin embargo, si realizas la división de polinomios primero, puedes transformar esta integral en una suma de integrales más simples. ¡Es como desmenuzar un problema grande en pedazos más manejables!
Pasos para Realizar la División de Polinomios
Paso 1: Configura la División
Comencemos con un ejemplo sencillo. Supongamos que queremos dividir el polinomio ( P(x) = 2x^3 + 3x^2 – x + 5 ) entre ( D(x) = x + 2 ). Primero, escribimos esto en forma de división larga.
1. Escribe ( P(x) ) dentro de la casita de la división y ( D(x) ) fuera.
2. Comienza dividiendo el primer término de ( P(x) ) por el primer término de ( D(x) ).
Paso 2: Realiza la División
En nuestro ejemplo, el primer término de ( P(x) ) es ( 2x^3 ) y el primer término de ( D(x) ) es ( x ). Así que:
[ frac{2x^3}{x} = 2x^2 ]
Ahora, multiplicamos ( 2x^2 ) por ( D(x) ):
[ 2x^2 cdot (x + 2) = 2x^3 + 4x^2 ]
Restamos esto de ( P(x) ):
[ (2x^3 + 3x^2 – x + 5) – (2x^3 + 4x^2) = -x^2 – x + 5 ]
Paso 3: Repite el Proceso
Ahora repetimos el proceso con el nuevo polinomio ( -x^2 – x + 5 ). Dividimos el primer término de ( -x^2 ) entre ( x ):
[ frac{-x^2}{x} = -x ]
Multiplicamos ( -x ) por ( D(x) ):
[ -x cdot (x + 2) = -x^2 – 2x ]
Restamos de nuestro polinomio:
[ (-x^2 – x + 5) – (-x^2 – 2x) = x + 5 ]
Paso 4: Continúa Hasta el Resto
Finalmente, repetimos el proceso una vez más. Dividimos ( x ) entre ( x ):
[ frac{x}{x} = 1 ]
Multiplicamos ( 1 ) por ( D(x) ):
[ 1 cdot (x + 2) = x + 2 ]
Restamos:
[ (x + 5) – (x + 2) = 3 ]
Ahora hemos terminado. El cociente es ( 2x^2 – x + 1 ) y el residuo es ( 3 ). Así que podemos escribir:
[ P(x) = (x + 2)(2x^2 – x + 1) + 3 ]
Integrando el Resultado
Una vez que hemos realizado la división, el siguiente paso es integrar el resultado. Ahora tenemos:
[ int frac{P(x)}{D(x)} , dx = int (2x^2 – x + 1) , dx + int frac{3}{x + 2} , dx ]
Esto se convierte en dos integrales separadas. La primera es bastante directa:
[ int (2x^2 – x + 1) , dx = frac{2}{3}x^3 – frac{1}{2}x^2 + x + C_1 ]
Y la segunda, que es una integral logarítmica:
[ int frac{3}{x + 2} , dx = 3 ln|x + 2| + C_2 ]
Finalmente, combinamos los resultados:
[ int frac{P(x)}{D(x)} , dx = frac{2}{3}x^3 – frac{1}{2}x^2 + x + 3 ln|x + 2| + C ]
Ejemplo Práctico Completo
Ahora que hemos revisado el proceso, veamos un ejemplo completo desde el principio hasta el final. Supongamos que queremos integrar:
[ int frac{x^3 + 4x^2 + 5x + 6}{x^2 + 2} , dx ]
1. División de Polinomios:
– Dividimos ( x^3 + 4x^2 + 5x + 6 ) por ( x^2 + 2 ).
– El cociente es ( x + 4 ) y el residuo es ( -2 ).
– Así que ( frac{x^3 + 4x^2 + 5x + 6}{x^2 + 2} = x + 4 – frac{2}{x^2 + 2} ).
2. Integración:
– Integramos cada término:
[ int (x + 4) , dx – int frac{2}{x^2 + 2} , dx ]
– La primera parte es sencilla:
[ frac{x^2}{2} + 4x + C_1 ]
– Para la segunda parte, recordemos que:
[ int frac{2}{x^2 + 2} , dx = sqrt{2} tan^{-1}left(frac{x}{sqrt{2}}right) + C_2 ]
Finalmente, combinamos todo:
[ int frac{x^3 + 4x^2 + 5x + 6}{x^2 + 2} , dx = frac{x^2}{2} + 4x – sqrt{2} tan^{-1}left(frac{x}{sqrt{2}}right) + C ]
Y ahí lo tienes. La integral por división de polinomios no solo simplifica la tarea de integración, sino que también te permite abordar problemas que, de otro modo, podrían parecer abrumadores. Al descomponer el proceso en pasos manejables, puedes ganar confianza y habilidad en el tema. Así que la próxima vez que te enfrentes a una integral complicada, recuerda que la división de polinomios puede ser tu mejor aliada.
¿Siempre necesito hacer la división de polinomios antes de integrar?
No siempre es necesario, pero si la integral es una fracción de polinomios, la división te ayudará a simplificar el proceso.
¿Qué hago si el residuo es cero?
Si el residuo es cero, eso significa que ( P(x) ) es divisible por ( D(x) ), y puedes integrar el cociente directamente.
¿Puedo aplicar la división de polinomios a funciones más complejas?
Sí, la técnica se puede aplicar a polinomios de mayor grado y a funciones racionales. La clave es siempre simplificar primero.
¿La integral por división de polinomios se aplica en cálculo avanzado?
Sí, esta técnica es fundamental en el cálculo integral y se utiliza en diversas áreas de matemáticas avanzadas, incluyendo el análisis y la teoría de funciones.
¿Hay alguna práctica recomendada para mejorar en esto?
¡Claro! La práctica constante es clave. Resuelve varios problemas de diferentes niveles de dificultad y no dudes en buscar ejemplos y ejercicios en libros de texto o en línea.
¡Espero que este artículo te haya sido útil y que ahora te sientas más seguro al enfrentar integrales que involucran división de polinomios!