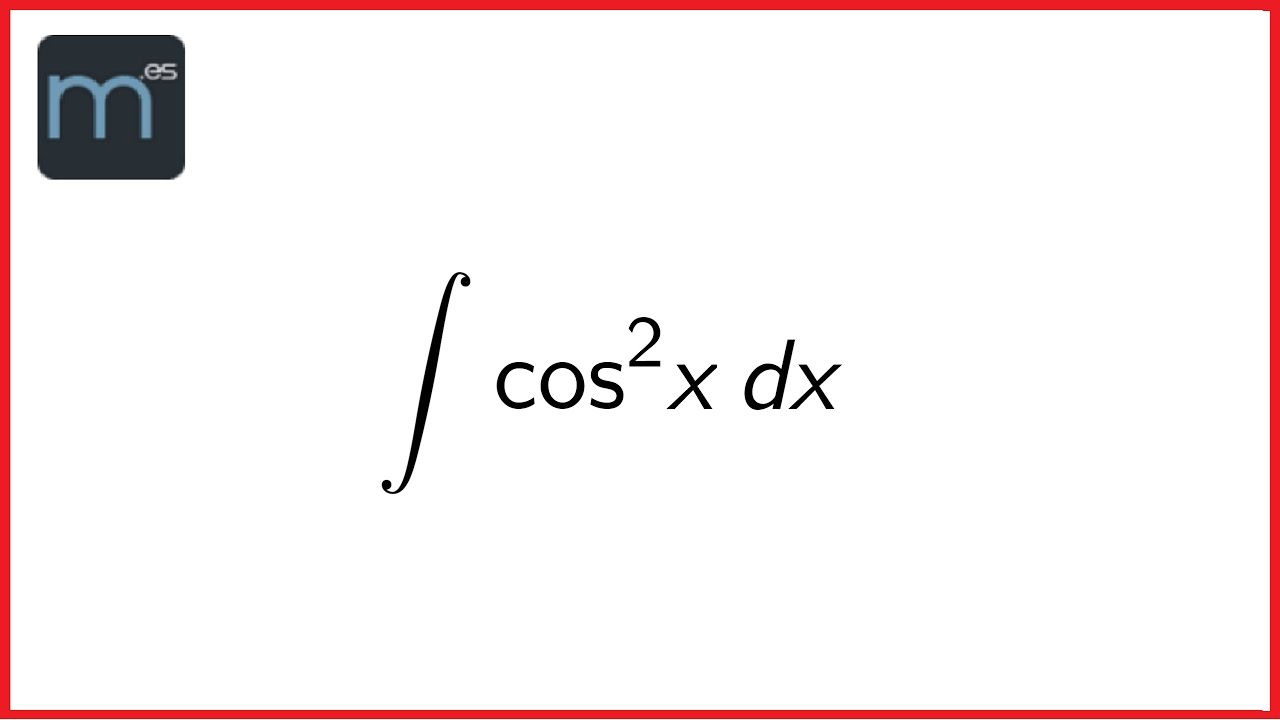¿Alguna vez te has preguntado cómo se resuelven las integrales de funciones trigonométricas? Si es así, ¡estás en el lugar correcto! Hoy vamos a sumergirnos en el fascinante mundo de la integral del coseno cuadrado de x, una función que aparece con frecuencia en cálculo y en diversas aplicaciones de la física y la ingeniería. No te preocupes si no eres un experto en matemáticas; aquí lo explicaremos todo paso a paso, de una manera sencilla y amigable.
¿Qué es la Integral del Coseno Cuadrado?
La integral del coseno cuadrado, representada como ∫ cos²(x) dx, puede parecer intimidante al principio, pero es solo otra forma de integrar funciones. Antes de lanzarnos a la resolución, es útil recordar que la integral es, en esencia, el área bajo la curva de una función. Así que, cuando hablamos de la integral del coseno cuadrado, estamos buscando el área bajo la curva de esta función específica. ¿Te suena más claro ahora? Genial, sigamos adelante.
La Identidad Fundamental: Coseno Cuadrado
Para resolver la integral del coseno cuadrado, es esencial conocer una identidad trigonométrica clave: la identidad de reducción de ángulo. Esta nos dice que:
cos²(x) = (1 + cos(2x)) / 2
Esta identidad es nuestra mejor amiga en este proceso, ya que nos permite transformar la función en algo más manejable. Al descomponer coseno cuadrado de esta manera, podemos simplificar la integral considerablemente. ¿Listo para ver cómo funciona?
Pasos para Resolver la Integral del Coseno Cuadrado
Paso 1: Aplicar la Identidad
Comencemos aplicando la identidad mencionada anteriormente a nuestra integral:
∫ cos²(x) dx = ∫ (1 + cos(2x)) / 2 dx
Esto simplifica nuestra tarea, ya que ahora tenemos una integral más sencilla que resolver. ¿Ves cómo empieza a tomar forma?
Paso 2: Separar la Integral
Ahora, podemos separar la integral en dos partes:
∫ (1/2) dx + ∫ (1/2) cos(2x) dx
Esto nos permitirá resolver cada parte de forma independiente. ¡Vamos a por ello!
Paso 3: Resolver las Integrales Individuales
Para la primera parte, la integral de 1/2 dx es simplemente (1/2)x. Fácil, ¿verdad? Ahora, para la segunda parte, utilizamos una regla básica de integración:
∫ cos(kx) dx = (1/k) sin(kx) + C
En nuestro caso, k es 2, así que:
∫ (1/2) cos(2x) dx = (1/4) sin(2x)
Ahora, combinando ambas partes, tenemos:
∫ cos²(x) dx = (1/2)x + (1/4) sin(2x) + C
Ejemplos Prácticos
Veamos un par de ejemplos para que puedas ver cómo aplicar esto en la práctica.
Ejemplo 1: Calcular ∫ cos²(3x) dx
Siguiendo los mismos pasos que antes, aplicamos la identidad:
∫ cos²(3x) dx = ∫ (1 + cos(6x)) / 2 dx
Separando la integral, obtenemos:
∫ (1/2) dx + ∫ (1/2) cos(6x) dx
Resolviendo cada parte:
Para la primera parte: (1/2)x
Para la segunda parte: (1/12) sin(6x)
Entonces, la solución es:
∫ cos²(3x) dx = (1/2)x + (1/12) sin(6x) + C
Ejemplo 2: Calcular ∫ cos²(θ) dθ
Ahora, probemos con un ejemplo diferente, usando la variable θ. Siguiendo el mismo proceso:
∫ cos²(θ) dθ = ∫ (1 + cos(2θ)) / 2 dθ
Separando la integral:
∫ (1/2) dθ + ∫ (1/2) cos(2θ) dθ
Resolviendo ambas partes:
Para la primera parte: (1/2)θ
Para la segunda parte: (1/4) sin(2θ)
Así que, la solución es:
∫ cos²(θ) dθ = (1/2)θ + (1/4) sin(2θ) + C
Aplicaciones de la Integral del Coseno Cuadrado
Ahora que ya sabemos cómo calcular la integral del coseno cuadrado, es interesante pensar en dónde podemos aplicarla. Esta integral tiene diversas aplicaciones en campos como la física, la ingeniería y hasta en la economía. Por ejemplo, en física, puede usarse para calcular el trabajo realizado en sistemas oscilatorios, donde el movimiento puede describirse con funciones trigonométricas.
Además, en ingeniería eléctrica, el coseno cuadrado se relaciona con la potencia media en circuitos de corriente alterna. ¿Te imaginas lo útil que es dominar esto? Ahora eres un paso más cerca de entender estos conceptos complejos.
¿Por qué se usa la identidad trigonométrica para resolver la integral?
Usamos la identidad trigonométrica para simplificar la función, haciéndola más manejable para la integración. Sin esta identidad, la integral sería mucho más complicada.
¿Existen otras formas de integrar cos²(x)?
Sí, hay otros métodos, como la integración por partes o el uso de series de Fourier, pero la identidad trigonométrica es generalmente la más sencilla y directa.
¿La integral del coseno cuadrado tiene alguna relación con otras funciones trigonométricas?
Definitivamente. Muchas funciones trigonométricas tienen identidades que pueden ser utilizadas para simplificar integrales, y el coseno cuadrado es solo una de ellas. Por ejemplo, también podemos ver la relación con el seno cuadrado a través de la identidad pitagórica.
¿Qué pasa si la integral tiene límites?
Si la integral tiene límites, simplemente evaluamos la función resultante en esos límites. Por ejemplo, para calcular ∫[a, b] cos²(x) dx, usaríamos el resultado anterior y luego calcularíamos F(b) – F(a), donde F es la función antiderivada que obtuvimos.
Ahora que tienes una comprensión sólida de la integral del coseno cuadrado, ¿qué tal si intentas resolver algunas integrales por tu cuenta? ¡Practicar es la mejor manera de aprender!