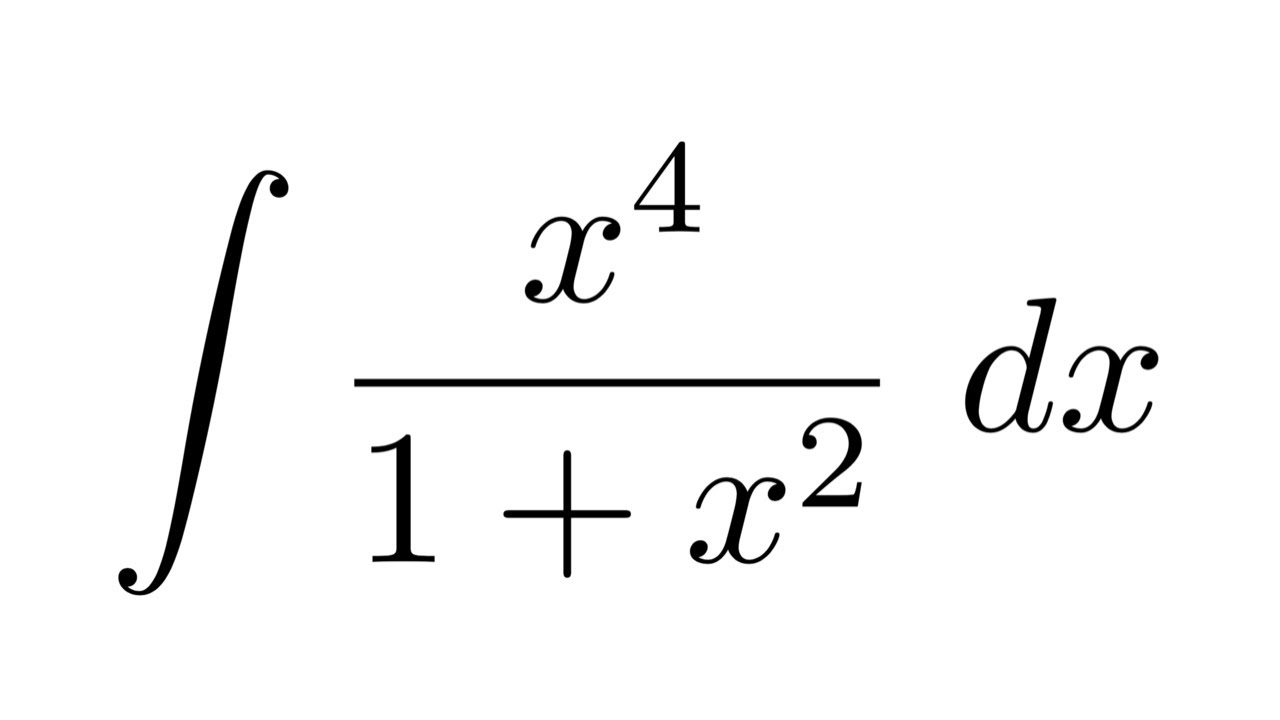¡Hola, amante de las matemáticas! Hoy vamos a sumergirnos en el fascinante mundo de las integrales, específicamente en cómo calcular la integral de x4. Si alguna vez te has preguntado cómo se hace o por qué es importante, estás en el lugar correcto. Las integrales son una herramienta fundamental en el cálculo que nos ayuda a entender áreas bajo curvas, volúmenes y muchas otras aplicaciones en la vida real. Así que, ¿listo para convertirte en un experto en integrales? ¡Vamos a ello!
¿Qué es una Integral?
Antes de entrar en materia, es esencial que comprendamos qué es una integral. Imagina que tienes una curva en un gráfico, y quieres saber cuánta área hay bajo esa curva. Eso es, en esencia, lo que hace una integral: calcula el área. En el caso de x4, queremos encontrar el área bajo la curva de esta función entre dos puntos. Pero no te preocupes, no necesitamos ser artistas para trazar la curva, ¡solo un poco de matemáticas!
La Integral Indefinida de x4
La integral de x4 se expresa matemáticamente como ∫ x4 dx. La «dx» al final simplemente indica que estamos integrando respecto a x. Para calcularla, utilizamos la regla de potencias de las integrales, que es bastante sencilla: si tienes x elevado a la n, la integral se calcula como x elevado a la n+1 dividido por n+1, más una constante de integración «C».
Aplicando la Regla de Potencias
Siguiendo esta regla, para x4, n es igual a 4. Así que, cuando aplicamos la regla, tenemos:
∫ x4 dx = (x4+1)/(4+1) + C = (x5)/5 + C.
¡Y ahí lo tienes! La integral indefinida de x4 es (x5)/5 + C. Pero, ¿qué significa esa «C»? Esa constante es crucial porque al integrar, estamos encontrando una familia de funciones que pueden diferir por una constante. Así que, aunque hayamos encontrado una solución, hay muchas más que también son correctas.
La Integral Definida de x4
Ahora que hemos visto la integral indefinida, hablemos de la integral definida. Imagina que ahora queremos encontrar el área bajo la curva de x4 entre dos puntos específicos, digamos desde x = 1 hasta x = 3. Para hacer esto, primero encontramos la integral indefinida como antes, y luego evaluamos esa función en los límites superior e inferior.
Evaluando la Integral Definida
Entonces, partimos de nuestra integral indefinida:
F(x) = (x5)/5 + C.
Ahora evaluamos F(3) y F(1):
F(3) = (35)/5 + C = 243/5 + C.
F(1) = (15)/5 + C = 1/5 + C.
Ahora, restamos F(1) de F(3):
Área = F(3) – F(1) = (243/5 + C) – (1/5 + C) = (243/5 – 1/5) = 242/5.
Así que el área bajo la curva de x4 desde x = 1 hasta x = 3 es 242/5 unidades cuadradas. ¡Impresionante, ¿no?!
Ejemplos Prácticos
Ahora que ya entendemos cómo calcular la integral de x4, vamos a practicar con algunos ejemplos más. La práctica es clave en matemáticas, y te ayudará a consolidar lo que has aprendido.
Ejemplo 1: Integral Indefinida
Calcula ∫ x4 dx. Como ya lo vimos, la respuesta es:
∫ x4 dx = (x5)/5 + C.
Ejemplo 2: Integral Definida
Calcula ∫02 x4 dx. Siguiendo el mismo procedimiento:
Primero, encontramos la integral indefinida:
F(x) = (x5)/5 + C.
Luego evaluamos en los límites:
F(2) = (25)/5 = 32/5,
F(0) = (05)/5 = 0.
Área = F(2) – F(0) = (32/5 – 0) = 32/5.
Aplicaciones de las Integrales
Las integrales no solo son un ejercicio académico, sino que tienen múltiples aplicaciones en la vida real. Desde calcular áreas de terrenos hasta encontrar el volumen de un objeto, las integrales son herramientas poderosas. También se utilizan en la física para encontrar el trabajo realizado por una fuerza variable o para determinar la carga eléctrica acumulada a lo largo de un conductor. Así que, la próxima vez que veas una integral, recuerda que no es solo un conjunto de símbolos, ¡es una forma de entender el mundo que nos rodea!
¿Por Qué Deberías Aprender a Integrar?
Aprender a integrar puede parecer complicado al principio, pero es una habilidad que te abrirá muchas puertas. Las matemáticas son la base de muchas disciplinas, desde la ingeniería hasta la economía, y tener un buen manejo de las integrales te dará una ventaja competitiva. Además, resolver integrales puede ser muy satisfactorio, como completar un rompecabezas complicado. ¿Quién no disfruta de esa sensación de logro?
Consejos para Aprender Integrales
Si estás empezando a aprender sobre integrales, aquí van algunos consejos prácticos:
- Practica Regularmente: La práctica hace al maestro. Cuanto más practiques, más cómodo te sentirás.
- Utiliza Recursos en Línea: Hay muchos tutoriales y videos en línea que pueden ofrecerte diferentes perspectivas y técnicas.
- No Te Desanimes: Al principio puede parecer difícil, pero con el tiempo y la práctica, te volverás más competente.
- Haz Preguntas: No dudes en preguntar a tus profesores o compañeros si tienes dudas. A veces, una pequeña aclaración puede hacer una gran diferencia.
¿Cuál es la diferencia entre integral indefinida y definida?
La integral indefinida se refiere a la familia de funciones que se derivan de una función dada, mientras que la integral definida calcula el área bajo la curva entre dos puntos específicos.
¿Por qué es importante la constante «C» en la integral indefinida?
La constante «C» representa la familia de funciones que son equivalentes a la función original, ya que todas estas funciones tienen la misma derivada.
¿Las integrales tienen aplicaciones en la vida real?
¡Sí! Las integrales se utilizan en muchas áreas, como la física, la economía, la biología y la ingeniería, para calcular áreas, volúmenes y otros valores importantes.
¿Cómo puedo mejorar en la resolución de integrales?
Practica con regularidad, busca recursos en línea y no dudes en hacer preguntas. Cuanto más tiempo dediques a entender los conceptos, más fácil te resultará resolver integrales.
¿Es necesario saber derivadas para entender integrales?
Sí, tener una comprensión básica de las derivadas es fundamental, ya que las integrales y derivadas son conceptos inversos en cálculo.
Y ahí lo tienes, amigo. Ahora estás más preparado para enfrentar el desafío de las integrales. Recuerda que la práctica es clave, así que sigue practicando y no te desanimes. ¡Buena suerte en tu viaje matemático!