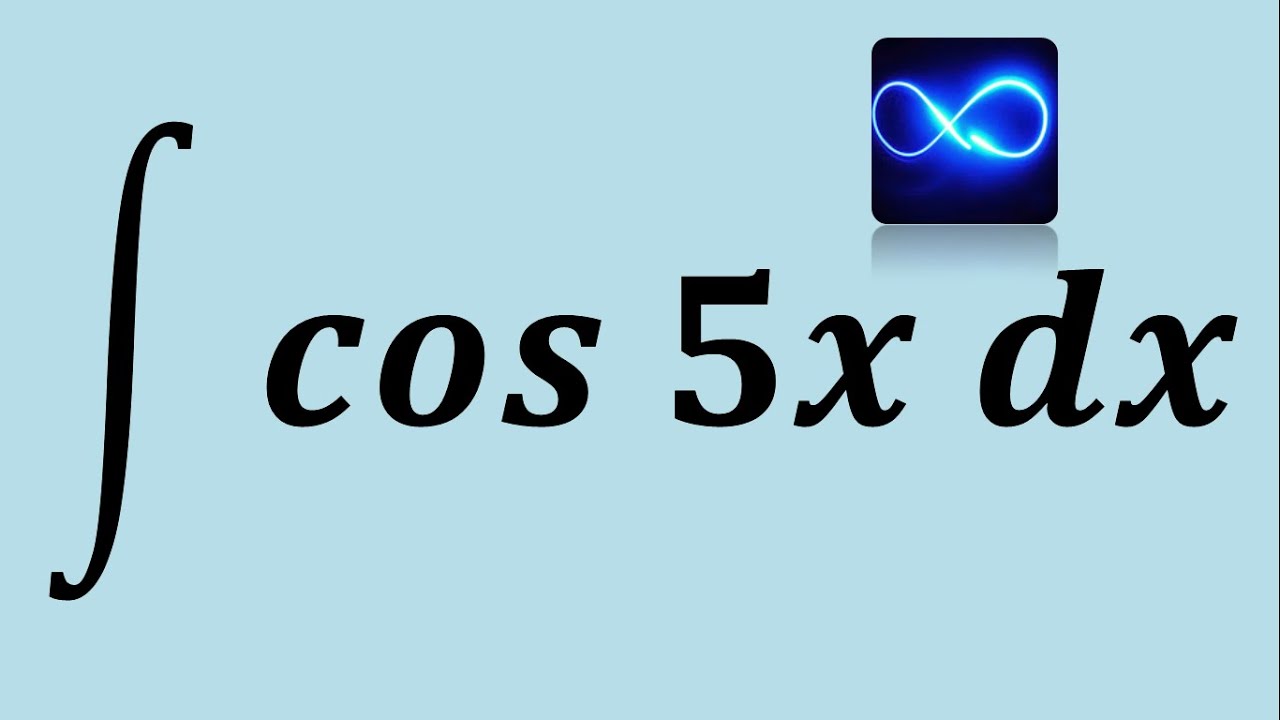Cuando te sumerges en el mundo del cálculo, una de las primeras cosas que te enseñan son las integrales. Y entre las funciones más importantes que se integran está el coseno. Pero, ¿alguna vez te has preguntado por qué es tan relevante? La integral de coseno no solo es una herramienta matemática, sino que también es fundamental en diversas aplicaciones en la física, la ingeniería y más. ¡Así que prepárate! Vamos a explorar este tema de manera sencilla y práctica.
¿Qué es la Integral de Coseno x?
La integral de coseno x, denotada comúnmente como ∫cos(x)dx, es una operación que busca encontrar la función cuya derivada es coseno. ¿Te suena complicado? No te preocupes, es más sencillo de lo que parece. La integral de coseno x es una de las integrales más básicas que puedes encontrar en cálculo, y su resultado es bastante limpio y directo.
La Fórmula Básica
La integral de coseno x se puede expresar de manera simple. El resultado de esta integral es:
∫cos(x)dx = sin(x) + C
Donde C representa la constante de integración. Esta C es importante porque, al integrar, hay infinitas funciones que podrían derivar en coseno x, y esta constante nos ayuda a tener en cuenta todas esas posibilidades. ¡Piensa en ella como una «sorpresa» que se añade al resultado!
¿Por qué es Importante la Integral de Coseno x?
La integral de coseno x no es solo un ejercicio académico. Su relevancia se extiende a varios campos. Por ejemplo, en física, se utiliza para describir movimientos oscilatorios, como el de un péndulo o una onda sonora. En ingeniería, puedes encontrarla en el análisis de circuitos eléctricos y en la teoría de señales. Así que, si alguna vez pensaste que aprender cálculo era solo un requisito escolar, ¡piénsalo de nuevo!
Visualizando la Integral de Coseno
Una buena manera de entender la integral de coseno es a través de su representación gráfica. Imagina que tienes una curva que representa la función coseno. Al integrar, lo que realmente estamos haciendo es calcular el área bajo esa curva entre dos puntos. Este concepto de área es clave en el cálculo y se puede visualizar como el espacio que se encuentra entre la curva y el eje x. Así que, cuando pienses en la integral, imagina que estás «llenando» un espacio con área. ¡Es como pintar un lienzo!
Ejemplos Prácticos de la Integral de Coseno x
Ahora que tenemos una idea básica, veamos algunos ejemplos prácticos para que puedas aplicar lo que has aprendido. Recuerda, la práctica es fundamental en matemáticas.
Ejemplo 1: Integral Definida
Supongamos que queremos calcular la integral definida de coseno x desde 0 hasta π/2. Esto se expresa como:
∫0π/2 cos(x) dx
Usamos la fórmula que mencionamos anteriormente:
∫cos(x) dx = sin(x) + C
Ahora, evaluamos los límites:
sin(π/2) - sin(0) = 1 - 0 = 1
Así que, la integral definida de coseno x de 0 a π/2 es igual a 1. ¡Fácil, verdad?
Ejemplo 2: Integral con una Función Compuesta
Imagina que queremos integrar coseno de 2x. Esto puede parecer un poco más complicado, pero no te asustes. La integral se vería así:
∫cos(2x) dx
Para resolverlo, usamos una técnica conocida como sustitución. Deja que u = 2x, entonces du = 2dx, lo que significa que dx = du/2. Ahora, la integral se transforma en:
(1/2)∫cos(u) du
Ahora, aplicamos la integral de coseno:
(1/2)sin(u) + C = (1/2)sin(2x) + C
Y ahí lo tienes, ¡una nueva función a partir de la integral de coseno!
Aplicaciones de la Integral de Coseno x
Ahora que hemos cubierto la teoría y algunos ejemplos, hablemos de las aplicaciones prácticas de la integral de coseno x. Como mencionamos antes, su uso se extiende a varios campos, pero aquí hay algunas aplicaciones específicas:
Física: Movimiento Oscilatorio
En física, el movimiento oscilatorio, como el de un péndulo, puede describirse usando funciones trigonométricas. La integral de coseno es crucial para determinar la posición en función del tiempo, ayudando a predecir el comportamiento de sistemas oscilantes.
Ingeniería: Análisis de Circuitos
Los ingenieros utilizan la integral de coseno en el análisis de circuitos eléctricos, especialmente en circuitos de corriente alterna. La comprensión de cómo varían las corrientes y voltajes a lo largo del tiempo es fundamental para diseñar sistemas eléctricos eficientes.
Gráficos y Diseño
En diseño gráfico y animación, las funciones trigonométricas son utilizadas para crear movimientos suaves y naturales. La integral de coseno puede ayudar a determinar trayectorias y patrones de movimiento en la creación de gráficos animados.
Consejos para Integrar Coseno x
Si bien la integral de coseno x es una de las más sencillas, aquí hay algunos consejos que te ayudarán a manejarla mejor:
Practica con Diferentes Límites
La práctica hace al maestro. Intenta calcular integrales definidas de coseno con diferentes límites para familiarizarte con el proceso. Cuanto más practiques, más confianza ganarás.
Usa Sustituciones Cuando Sea Necesario
Si te encuentras con integrales más complejas, no dudes en usar sustituciones. Esto puede simplificar el problema y hacerlo más manejable. Recuerda, ¡la creatividad es clave en matemáticas!
Visualiza las Funciones
Siempre que sea posible, visualiza las funciones que estás integrando. Dibuja las gráficas y observa cómo se relacionan. Esto no solo te ayudará a entender mejor el concepto, sino que también hará que el aprendizaje sea más divertido.
1. ¿Cuál es la integral de coseno x en términos de seno?
La integral de coseno x es sin(x) + C. Esto significa que la función cuya derivada es coseno es el seno.
2. ¿Qué sucede si integro coseno con límites?
Cuando integras coseno con límites, obtienes un valor numérico que representa el área bajo la curva de la función coseno entre esos límites.
3. ¿Puedo aplicar la integral de coseno en problemas de la vida real?
¡Definitivamente! La integral de coseno se utiliza en física, ingeniería y muchos otros campos, por lo que es muy relevante en situaciones del mundo real.
4. ¿Existen otras funciones trigonométricas que se integran de manera similar?
Sí, funciones como seno, tangente y secante también tienen integrales que se pueden calcular de manera similar, cada una con sus propias fórmulas y resultados.
5. ¿Cómo puedo mejorar en la integración de funciones trigonométricas?
La práctica es clave. Trabaja en problemas variados, utiliza recursos en línea y no dudes en pedir ayuda si te sientes atascado. Con el tiempo, mejorarás en la integración de funciones trigonométricas.
Así que ahí lo tienes, una guía completa sobre la integral de coseno x. Desde su definición hasta ejemplos prácticos y aplicaciones, esperamos que este artículo te haya ayudado a entender mejor este concepto fundamental. ¡Sigue practicando y explorando el fascinante mundo del cálculo!