¿Alguna vez te has encontrado frente a una gráfica llena de flechas y no has tenido ni idea de qué significan? No te preocupes, estás en el lugar correcto. En esta guía, vamos a desglosar cómo interpretar la gráfica de suma de vectores de una manera sencilla y comprensible. La suma de vectores es un concepto fundamental en física y matemáticas, y entender cómo se representa gráficamente puede abrirte un mundo de posibilidades. Así que, siéntate, relájate y acompáñame en este viaje a través de la gráfica de suma de vectores.
¿Qué es un Vector?
Primero lo primero: ¿qué es un vector? Imagina que estás dando instrucciones a un amigo sobre cómo llegar a un lugar. Podrías decirle «ve hacia el norte 10 metros y luego gira a la derecha y camina 5 metros». Eso es un poco lo que hace un vector. Es una entidad que tiene una dirección y una magnitud. En términos más técnicos, un vector se representa como una flecha en un plano, donde la longitud de la flecha indica la magnitud y la dirección de la flecha indica hacia dónde va. ¿Ves? No es tan complicado, ¿verdad?
¿Por Qué Es Importante la Suma de Vectores?
La suma de vectores es crucial porque en el mundo real, muchas fuerzas y movimientos se pueden descomponer en vectores. Por ejemplo, si un barco navega en una dirección y el viento sopla en otra, puedes sumar esos vectores para determinar la dirección y velocidad real del barco. Así que, entender cómo sumar vectores no solo es útil en el aula, sino que también tiene aplicaciones prácticas en la vida cotidiana.
El Método Gráfico para Sumar Vectores
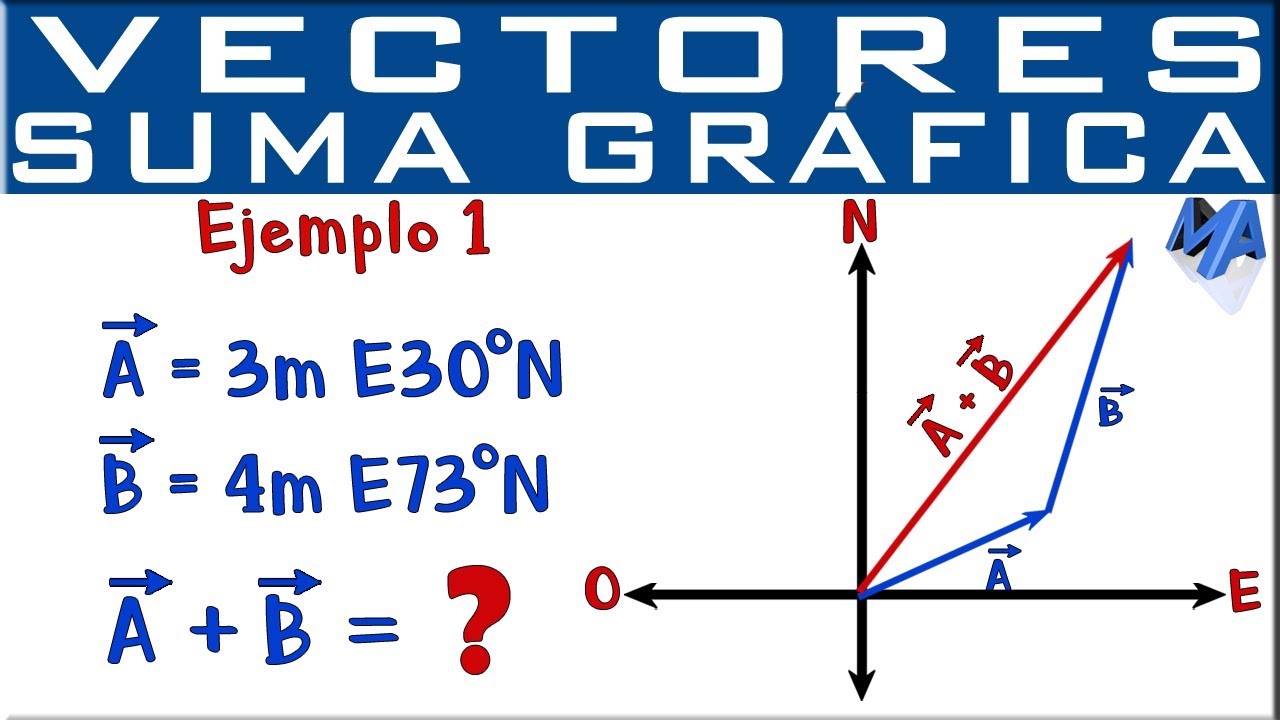
Ahora que ya sabemos qué es un vector y por qué es importante, hablemos sobre cómo se suman gráficamente. La forma más común de sumar vectores es el método de la «cabeza a cola». Imagina que tienes dos vectores, A y B. Para sumarlos, dibujas el vector A y luego colocas el vector B comenzando en la «cabeza» del vector A. La línea que va desde la «cola» de A hasta la «cabeza» de B te dará el vector resultante, que llamaremos R. Este método es visual y te permite ver claramente cómo se combinan las direcciones y magnitudes de los vectores.
Elementos de una Gráfica de Vectores
Para entender una gráfica de suma de vectores, hay algunos elementos clave que debes conocer. En primer lugar, cada vector se representa como una flecha, donde la longitud de la flecha indica su magnitud y la dirección indica hacia dónde se está moviendo. Además, las escalas en los ejes son importantes; una mala interpretación de la escala puede llevar a resultados incorrectos. Así que, siempre asegúrate de que estás viendo la gráfica correctamente.
Escalas y Unidades
Las escalas en los ejes son fundamentales. Por ejemplo, si un eje está marcado en metros y el otro en kilómetros, deberás tener cuidado al sumar los vectores. Asegúrate de que todos los vectores estén en las mismas unidades antes de realizar la suma. Esto puede parecer tedioso, pero es esencial para obtener resultados precisos. Piensa en ello como tener una receta de cocina: si usas tazas en lugar de mililitros, el resultado final podría ser desastroso.
Ejemplo Práctico de Suma de Vectores
Ahora, vamos a poner en práctica lo que hemos aprendido. Supongamos que tienes dos vectores: A (5 unidades hacia el este) y B (3 unidades hacia el norte). Para sumar estos vectores gráficamente, dibuja primero el vector A. Luego, desde la cabeza de A, dibuja el vector B. El vector resultante R se obtendrá al trazar una línea desde la cola de A hasta la cabeza de B. Ahora, usando el teorema de Pitágoras, podemos calcular la magnitud de R. ¿Te das cuenta de lo sencillo que es? Todo se reduce a unos simples pasos.
Interpretando el Resultado
Una vez que has encontrado el vector resultante, es hora de interpretarlo. La dirección de R te dará una idea clara de hacia dónde se está moviendo el objeto resultante de la suma de los vectores. Y la magnitud te dirá qué tan rápido o fuerte es ese movimiento. Es como si tuvieras un mapa que te dice no solo hacia dónde ir, sino también qué tan lejos está el destino. ¿No es genial?
Aplicaciones en el Mundo Real
La suma de vectores no solo se aplica en situaciones teóricas, sino que tiene muchas aplicaciones en la vida real. Por ejemplo, en ingeniería, cuando se diseñan estructuras, se debe considerar la suma de fuerzas que actúan sobre ellas. En deportes, los entrenadores analizan los vectores de velocidad y dirección para mejorar el rendimiento de los atletas. Cada vez que realizamos un movimiento, ya sea caminando, corriendo o incluso lanzando una pelota, estamos interactuando con vectores. Así que, la próxima vez que hagas algo físico, piensa en los vectores que están en juego.
Consejos para Mejorar en la Suma de Vectores
Si te sientes un poco abrumado por todo esto, no te preocupes. Aquí hay algunos consejos que pueden ayudarte a mejorar en la suma de vectores:
- Practica con ejemplos visuales: Cuanto más practiques, más cómodo te sentirás. Usa papel milimetrado o aplicaciones en línea para dibujar vectores.
- Haz uso de la tecnología: Existen muchas aplicaciones y herramientas en línea que te permiten manipular vectores y ver los resultados en tiempo real.
- Estudia en grupo: A veces, discutir con otros puede ayudarte a entender mejor los conceptos. La enseñanza entre pares es una herramienta poderosa.
La interpretación de la gráfica de suma de vectores es una habilidad valiosa que te ayudará en muchos aspectos de la ciencia y la vida cotidiana. Al comprender los conceptos básicos de los vectores y cómo sumarlos gráficamente, puedes tomar decisiones más informadas y resolver problemas de manera más efectiva. Recuerda que la práctica hace al maestro. Así que sigue practicando y no dudes en volver a esta guía cuando lo necesites. ¡Buena suerte en tu viaje a través del mundo de los vectores!
¿Puedo sumar vectores de diferentes magnitudes y direcciones?
Sí, puedes sumar vectores de diferentes magnitudes y direcciones, pero debes hacerlo teniendo en cuenta su dirección y usando el método adecuado para obtener un resultado preciso.
¿Qué herramientas puedo usar para practicar la suma de vectores?
Existen aplicaciones en línea, software de matemáticas y papel milimetrado que te pueden ayudar a practicar la suma de vectores de manera efectiva.
¿Es necesario conocer trigonometría para sumar vectores?
No es estrictamente necesario, pero conocer trigonometría puede facilitar el proceso, especialmente cuando se trata de calcular la magnitud y dirección de vectores resultantes.
¿Cómo afecta la dirección de los vectores al resultado final?
La dirección de los vectores es crucial porque determina cómo se combinan. Dos vectores que apuntan en direcciones opuestas pueden cancelarse, mientras que aquellos que apuntan en la misma dirección se sumarán.
¿Hay alguna diferencia entre la suma gráfica y la suma algebraica de vectores?
Sí, la suma gráfica te da una representación visual y es útil para comprender la interacción de vectores, mientras que la suma algebraica utiliza componentes numéricas para obtener resultados más precisos.