¿Qué es una Función Constante y Por Qué es Importante?
La función constante es uno de esos conceptos en matemáticas que, aunque parecen simples, tienen un impacto enorme en diversas áreas, desde la economía hasta la física. Pero, ¿qué es exactamente una función constante? En términos sencillos, es una función que siempre devuelve el mismo valor, sin importar el input que se le dé. Imagina que estás en una fiesta, y cada vez que alguien te pregunta «¿Cuánto cuesta la entrada?», tu respuesta siempre es la misma: «Diez euros». Esa es una función constante en acción. La gráfica de una función constante es una línea horizontal en el plano cartesiano, lo que significa que no importa cuánto cambie la variable independiente, el resultado permanece inalterado.
Ahora bien, no podemos subestimar la importancia de esta función. En la vida real, las funciones constantes son útiles para modelar situaciones donde no hay variabilidad. Por ejemplo, en finanzas, si tienes un ahorro que no cambia de valor, podrías utilizar una función constante para describirlo. Pero no nos quedemos ahí; hay mucho más que explorar. Así que, ¡sigue leyendo y descubre ejemplos concretos y aplicaciones fascinantes de las funciones constantes!
Definición y Características de la Función Constante
Para entender mejor qué es una función constante, vamos a desglosar su definición y características. Una función constante se puede expresar matemáticamente como:
f(x) = c
donde c es un número real constante. Esta simple ecuación nos dice que no importa el valor de x, el resultado siempre será c. Por ejemplo, si tomamos f(x) = 5, sin importar qué valor le des a x, el resultado siempre será 5. Esto significa que la función no tiene pendiente; es decir, no hay cambio en el valor de salida a medida que se modifica el valor de entrada.
Gráfica de la Función Constante
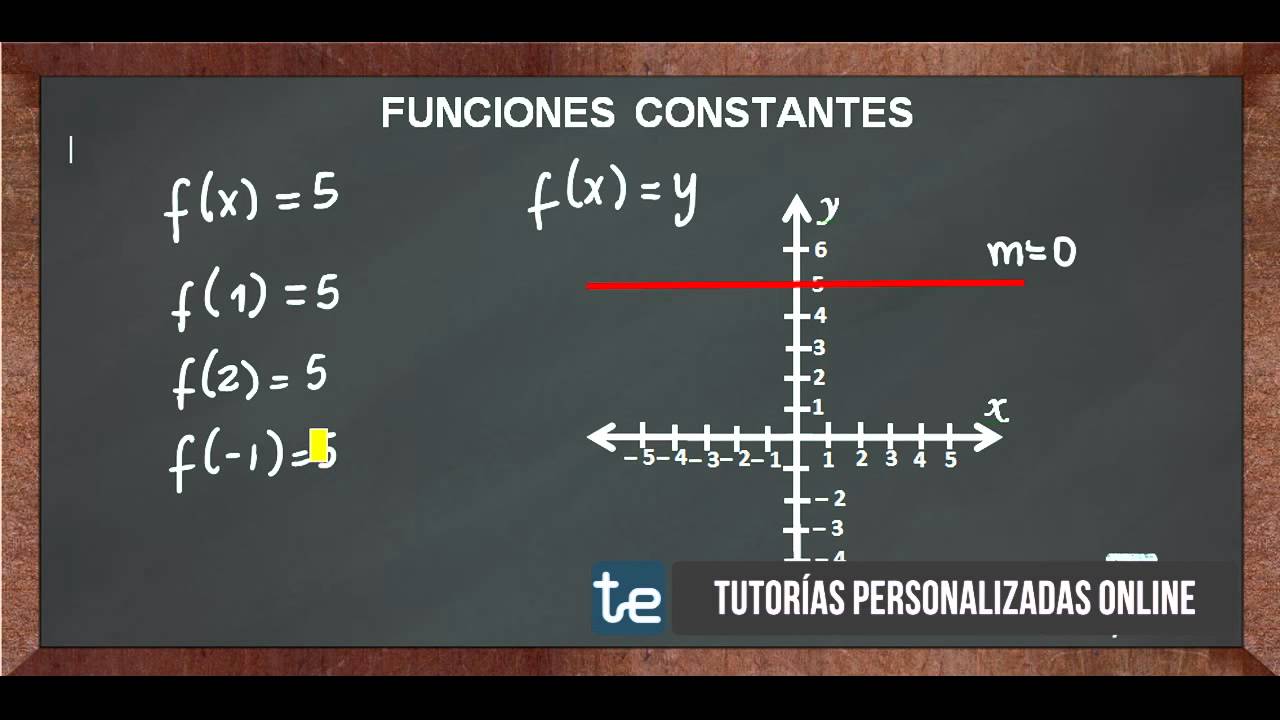
Si visualizas la gráfica de una función constante, verás que es una línea horizontal. Esto se debe a que, como mencionamos antes, el valor de salida no cambia, sin importar lo que hagas con el valor de entrada. Por ejemplo, si dibujas la función f(x) = 3, tu gráfico será una línea que cruza el eje y en 3 y se extiende de manera horizontal hacia ambos lados. Es como una carretera recta y plana: no importa cuánto avances, siempre estarás al mismo nivel.
Ejemplos Prácticos de Función Constante
Ahora que tenemos una buena comprensión de lo que es una función constante, veamos algunos ejemplos prácticos. ¿Te has preguntado alguna vez cómo se aplican estas funciones en situaciones cotidianas? Aquí van algunos ejemplos:
Ejemplo 1: Costo de un Producto
Imagina que estás en una tienda y decides comprar una botella de agua. El precio es siempre el mismo: 1 euro. Si representamos esto matemáticamente, podríamos decir que:
f(x) = 1
Donde x podría ser cualquier número que represente la cantidad de botellas que decides comprar. No importa cuántas compres, el precio por botella sigue siendo 1 euro. Este es un claro ejemplo de una función constante, donde el precio no cambia.
Ejemplo 2: Temperatura en un Refrigerador
Otro ejemplo que podría ser más cercano a tu día a día es la temperatura dentro de un refrigerador. Supongamos que tu refrigerador está configurado para mantener una temperatura constante de 4 grados Celsius. Esto se puede representar como:
f(x) = 4
Sin importar cuánto tiempo dejes la puerta abierta o cuántos alimentos agregues, la temperatura debería mantenerse en 4 grados, gracias a la regulación del aparato. Aquí, la función constante representa un sistema diseñado para mantener un valor fijo.
Aplicaciones en Diversas Áreas
Las funciones constantes no solo son útiles en situaciones cotidianas, sino que también tienen aplicaciones en diversas disciplinas. Aquí hay algunas áreas donde puedes encontrar estas funciones en acción:
En Economía
En economía, las funciones constantes son esenciales para modelar ciertos escenarios. Por ejemplo, si una empresa tiene un costo fijo mensual de 500 euros, independientemente de cuántos productos venda, podríamos representar este costo como:
f(x) = 500
Esto ayuda a las empresas a entender su estructura de costos y a tomar decisiones informadas sobre precios y producción.
En Ciencias Naturales
En física, la función constante puede describir fenómenos donde ciertos parámetros no cambian. Por ejemplo, la aceleración debida a la gravedad en la Tierra es aproximadamente 9.81 m/s². Este valor es constante en la superficie terrestre y puede ser representado como:
f(x) = 9.81
Esto es crucial para cálculos en mecánica y para entender cómo los objetos se comportan bajo la influencia de la gravedad.
Ventajas y Desventajas de las Funciones Constantes
Como todo en la vida, las funciones constantes tienen sus ventajas y desventajas. Vamos a echar un vistazo a ambas.
Ventajas
- Simplicidad: Las funciones constantes son fáciles de entender y trabajar con ellas, lo que las hace ideales para principiantes.
- Previsibilidad: Al ser constantes, puedes prever el resultado sin complicaciones, lo que es útil en situaciones financieras y de planificación.
- Modelado de Situaciones Estables: Son perfectas para modelar situaciones donde no hay cambios, como en costos fijos o condiciones ambientales estables.
Desventajas
- Limitación: Las funciones constantes no pueden capturar la complejidad del mundo real donde las variables cambian constantemente.
- Falta de Dinamismo: No son útiles para describir fenómenos que requieren variabilidad, como la oferta y la demanda en economía.
- Inflexibilidad: En situaciones donde se requiere un análisis más complejo, una función constante puede resultar insuficiente.
Ejercicios para Practicar
Ahora que hemos cubierto bastante sobre las funciones constantes, ¿por qué no intentas practicar un poco? Aquí te dejo algunos ejercicios que puedes resolver:
- 1. Si f(x) = 10, ¿cuál es el valor de f(50)?
- 2. Un restaurante cobra un cargo fijo de 15 euros por el servicio de entrega. Escribe la función que represente este costo.
- 3. La presión en una botella de gas se mantiene constante en 2 atmósferas. Escribe la función que describa esta situación.
Las funciones constantes pueden parecer simples, pero son fundamentales en muchos aspectos de nuestras vidas. Desde la economía hasta la física, estas funciones nos permiten modelar situaciones donde los valores no cambian, dándonos una base sólida para entender conceptos más complejos. Así que la próxima vez que te enfrentes a una función constante, recuerda que detrás de esa simplicidad hay un mundo de aplicaciones y utilidades. ¿Qué otros ejemplos de funciones constantes puedes pensar en tu vida diaria? ¡Déjanos tus pensamientos!
¿Las funciones constantes son útiles en programación?
¡Definitivamente! En programación, las funciones constantes pueden ser utilizadas para establecer valores predeterminados o constantes que no cambian a lo largo de la ejecución del programa.
¿Se pueden tener funciones constantes en otras dimensiones?
Sí, puedes tener funciones constantes en múltiples dimensiones. Por ejemplo, en un gráfico 3D, podrías tener una función constante que se mantenga en un plano específico.
¿Cómo se relacionan las funciones constantes con otras funciones matemáticas?
Las funciones constantes son un caso particular de funciones, y pueden ser consideradas como funciones lineales donde la pendiente es cero. Esto las relaciona con una amplia variedad de funciones matemáticas más complejas.
¿Pueden las funciones constantes cambiar con el tiempo?
No, por definición, una función constante no cambia con el tiempo o con el valor de entrada. Si comienza a variar, ya no sería una función constante.