Las funciones con radicales son un tema fascinante en el mundo de las matemáticas. Imagina que estás en una montaña rusa, y cada vuelta y cada caída te lleva a un nuevo descubrimiento. Así es cómo se siente explorar el universo de las funciones radicales. Pero, ¿qué son exactamente? En términos simples, una función radical es aquella que incluye una raíz, ya sea cuadrada, cúbica o de cualquier otro tipo. Por ejemplo, la función f(x) = √x es una de las más simples, pero su impacto en el aprendizaje matemático es enorme. En este artículo, desglosaremos todo lo que necesitas saber sobre las funciones con radicales: su definición, ejemplos, aplicaciones, y mucho más. ¡Así que abróchate el cinturón y prepárate para este viaje matemático!
¿Qué es una Función Radical?
Para entender mejor las funciones con radicales, primero debemos definir qué son. Una función radical es cualquier función que involucra una raíz. La forma más común es la raíz cuadrada, pero también podemos encontrar raíces cúbicas, cuartas, y así sucesivamente. La función más simple que puedes encontrar es f(x) = √x, que significa que tomamos la raíz cuadrada de x. Ahora, ¿por qué son tan importantes estas funciones? Porque nos ayudan a resolver ecuaciones que de otra manera serían difíciles de manejar. Las raíces nos permiten encontrar soluciones a problemas complejos de una manera más sencilla, casi como encontrar la salida de un laberinto.
Características de las Funciones Radicales
Dominio y Rango
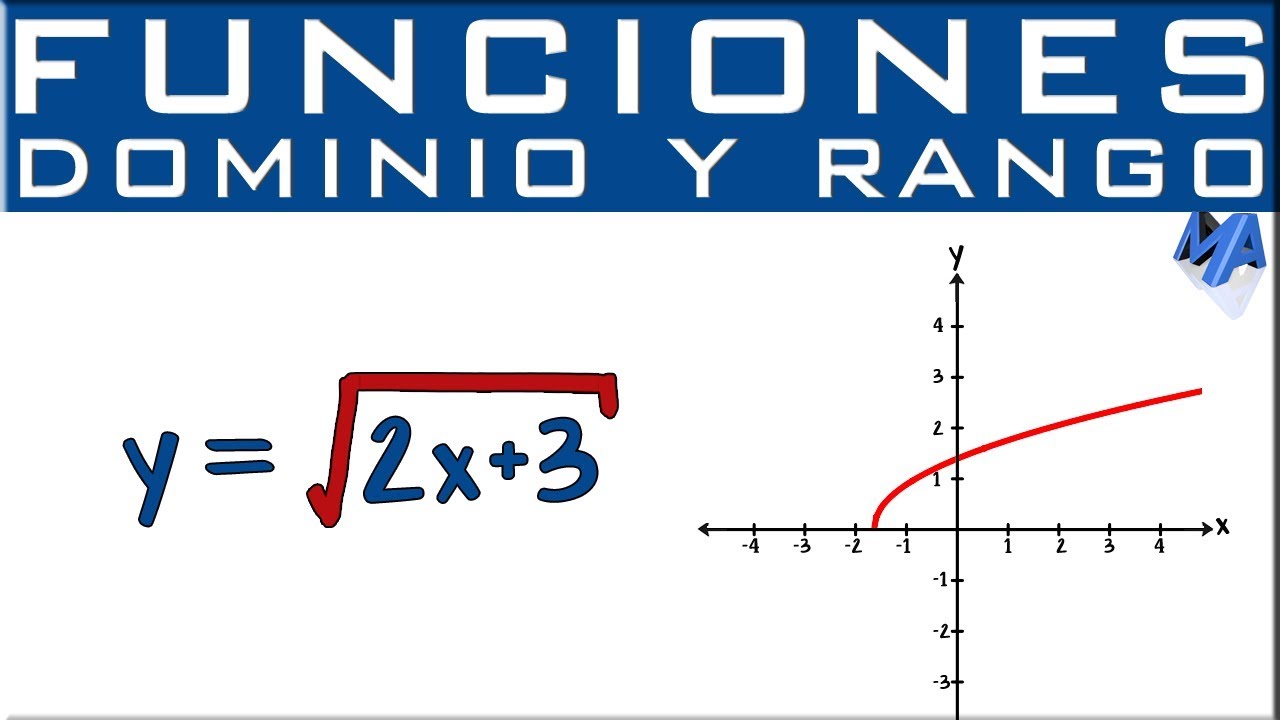
Una de las primeras cosas que debes considerar al trabajar con funciones radicales es su dominio y rango. El dominio se refiere a los valores que puedes ingresar en la función, mientras que el rango son los valores que puedes obtener. Por ejemplo, en la función f(x) = √x, el dominio es x ≥ 0, ya que no puedes tomar la raíz cuadrada de un número negativo en el conjunto de los números reales. El rango, por otro lado, es f(x) ≥ 0, ya que no puedes obtener un resultado negativo al aplicar la raíz cuadrada. Es como tener una caja de herramientas: necesitas saber qué herramientas puedes usar (dominio) y qué puedes construir con ellas (rango).
Comportamiento Gráfico
El gráfico de una función radical tiene características únicas. Por ejemplo, el gráfico de f(x) = √x comienza en el origen (0,0) y se extiende hacia la derecha, aumentando lentamente. Si dibujas el gráfico, notarás que nunca toca el eje negativo del y, lo que refleja que la función nunca dará valores negativos. Es como si la función estuviera corriendo por una pista, siempre buscando el camino hacia arriba, pero sin desviarse hacia abajo. Además, a medida que x aumenta, el aumento en y se ralentiza, lo que significa que la función se aplana. Esto es fundamental para entender cómo se comportan estas funciones en diferentes intervalos.
Ejemplos de Funciones Radicales
Ejemplo 1: Raíz Cuadrada
Consideremos la función f(x) = √(x + 2). Aquí, hemos desplazado la función raíz cuadrada hacia la izquierda en 2 unidades. El dominio ahora es x ≥ -2, ya que no puedes tener un número negativo dentro de la raíz. Si trazas este gráfico, verás que comienza en el punto (-2, 0) y sigue hacia la derecha, manteniendo el mismo comportamiento creciente de la raíz cuadrada. Este pequeño desplazamiento es como mover un cuadro en un tablero de ajedrez: el juego sigue, pero la posición ha cambiado.
Ejemplo 2: Raíz Cúbica
Ahora, hablemos de una función radical diferente: f(x) = ∛(x). La raíz cúbica es especial porque puedes tomar la raíz cúbica de cualquier número, positivo o negativo. Así que el dominio y el rango de esta función son todos los números reales. El gráfico de esta función es simétrico respecto al origen, lo que significa que si giras la gráfica 180 grados, se verá igual. Es como un espejo: lo que ves de un lado, también lo verás del otro. Esto le da a la raíz cúbica un carácter único que la diferencia de la raíz cuadrada.
Aplicaciones de las Funciones Radicales
Resolución de Problemas en Física
Las funciones radicales tienen muchas aplicaciones en el mundo real, especialmente en la física. Por ejemplo, la fórmula para la distancia recorrida por un objeto en caída libre está relacionada con la raíz cuadrada. La distancia d que un objeto cae en t segundos se puede expresar como d = 1/2 * g * t², donde g es la aceleración debida a la gravedad. Si quisieras despejar t, tendrías que tomar la raíz cuadrada, lo que te lleva a la función radical. Aquí, las matemáticas no son solo números; son herramientas que nos ayudan a entender el mundo que nos rodea.
Uso en la Arquitectura y el Diseño
Otro lugar donde las funciones radicales son útiles es en la arquitectura y el diseño. Por ejemplo, al calcular las dimensiones de un edificio, los arquitectos a menudo necesitan usar raíces para determinar las proporciones adecuadas. Si deseas diseñar una estructura que sea estéticamente agradable y funcional, comprender cómo se relacionan las dimensiones a través de funciones radicales puede ser esencial. Es como armar un rompecabezas: cada pieza debe encajar perfectamente para que el diseño final sea atractivo y estable.
Las funciones con radicales son una parte integral de las matemáticas y tienen aplicaciones prácticas en diversas disciplinas. Desde la física hasta la arquitectura, su presencia es omnipresente. Al aprender sobre estas funciones, no solo estamos adquiriendo conocimientos matemáticos, sino que también estamos abriendo puertas a nuevas formas de entender y resolver problemas en el mundo real. Entonces, la próxima vez que te encuentres con una función radical, recuerda que estás ante una herramienta poderosa que puede ayudarte a desentrañar los misterios de la naturaleza y la construcción. ¿No es emocionante pensar en todo lo que puedes lograr con un poco de matemáticas?
¿Cuál es la diferencia entre una raíz cuadrada y una raíz cúbica?
La raíz cuadrada se refiere a encontrar un número que, multiplicado por sí mismo, te dé el número original, mientras que la raíz cúbica busca un número que, multiplicado por sí mismo tres veces, te dé el número original. Así que, en esencia, la raíz cuadrada es un caso especial de la raíz cúbica.
¿Cómo se puede graficar una función radical?
Para graficar una función radical, primero determina su dominio y rango. Luego, calcula algunos puntos clave y traza esos puntos en un sistema de coordenadas. Asegúrate de observar el comportamiento de la función en diferentes intervalos para obtener una representación precisa.
¿Las funciones radicales siempre tienen un dominio limitado?
No necesariamente. Las funciones de raíz cúbica, por ejemplo, tienen un dominio que abarca todos los números reales. Sin embargo, las funciones de raíz cuadrada sí tienen un dominio limitado a los números no negativos.
¿Por qué son importantes las funciones radicales en la vida cotidiana?
Las funciones radicales son fundamentales en muchas áreas, como la ingeniería, la arquitectura y la física. Nos ayudan a modelar y resolver problemas reales, desde la construcción de edificios hasta el estudio del movimiento de los objetos.
¿Qué otros tipos de funciones matemáticas se relacionan con las funciones radicales?
Las funciones polinómicas, exponenciales y logarítmicas a menudo se relacionan con funciones radicales. Muchas veces, se pueden transformar entre ellas mediante operaciones algebraicas, lo que las convierte en herramientas útiles en el análisis matemático.