¡Hola! ¿Alguna vez te has preguntado cómo funciona un plano inclinado? Ese objeto tan simple que ves en la vida diaria, desde una rampa hasta una colina, es un ejemplo clásico en la física. A lo largo de este artículo, vamos a desmenuzar el concepto del plano inclinado a través de ejercicios resueltos que no solo te ayudarán a entender mejor el tema, sino que también te permitirán aplicar lo aprendido en situaciones reales. Así que, siéntate cómodo y prepárate para sumergirte en el fascinante mundo de la física. ¡Vamos a ello!
¿Qué es un Plano Inclinado?
Un plano inclinado es una superficie que forma un ángulo con respecto a la horizontal. Imagina que estás en un parque y ves una rampa para patinar. Esa rampa es un plano inclinado. La razón por la que es tan interesante en la física es que permite estudiar cómo se mueven los objetos bajo la influencia de la gravedad. A medida que un objeto se desliza por un plano inclinado, se descompone la fuerza de gravedad en dos componentes: una que actúa paralela al plano y otra perpendicular a él. ¡Interesante, ¿verdad?!
Componentes de Fuerza en el Plano Inclinado
Descomposición de Fuerzas
Para entender cómo funciona un plano inclinado, es crucial conocer cómo se descomponen las fuerzas. Imagina que tienes un bloque de madera en un plano inclinado. La fuerza de gravedad (Fg) actúa hacia abajo, pero podemos dividirla en dos partes. La componente que actúa paralela al plano (Fg, paralelo) es la que hará que el bloque se deslice hacia abajo. Por otro lado, la componente perpendicular (Fg, perpendicular) es la que empuja el bloque contra el plano.
La fórmula para calcular estas componentes es:
- Fg, paralelo = m * g * sen(θ)
- Fg, perpendicular = m * g * cos(θ)
Donde:
- m = masa del objeto
- g = aceleración debido a la gravedad (aproximadamente 9.81 m/s²)
- θ = ángulo del plano inclinado
Ejemplo Práctico 1: Cálculo de Fuerzas en un Plano Inclinado
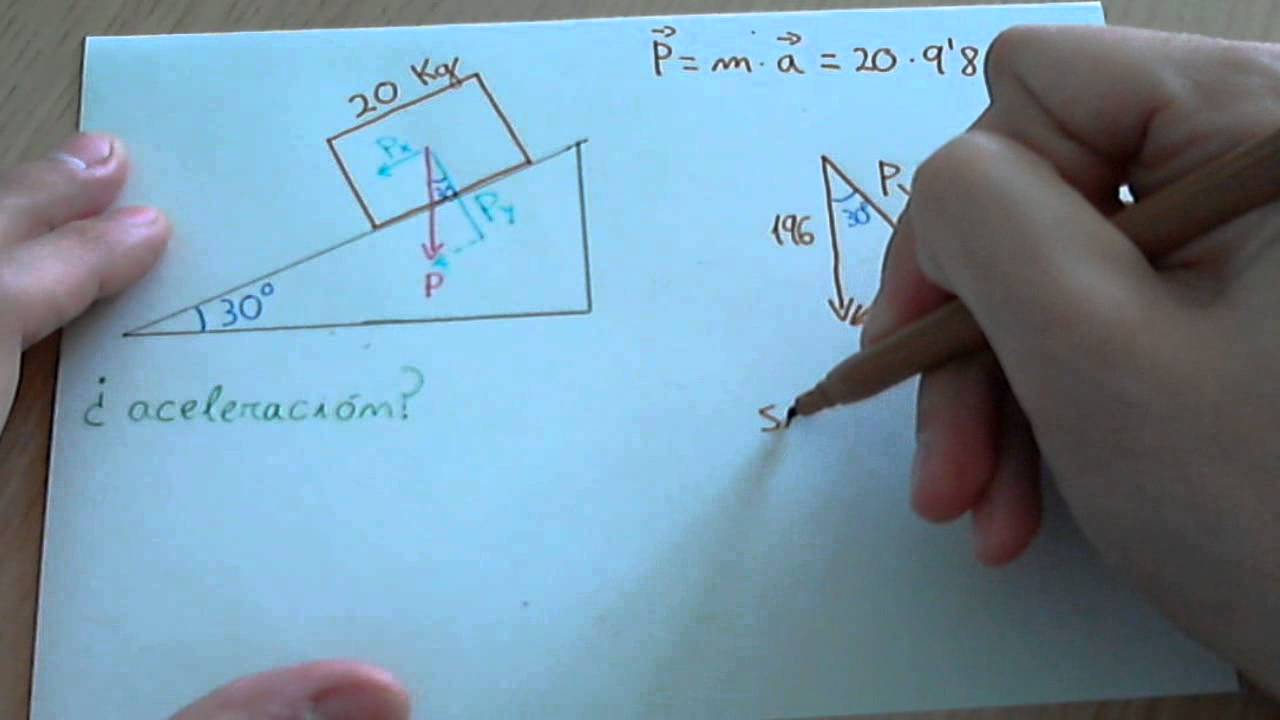
Supongamos que tenemos un bloque de 5 kg en un plano inclinado que forma un ángulo de 30 grados con la horizontal. ¿Cómo calculamos las fuerzas que actúan sobre él?
Primero, calculemos la fuerza de gravedad:
Fg = m * g = 5 kg * 9.81 m/s² = 49.05 N
Ahora, descomponemos esta fuerza:
Fg, paralelo = 49.05 N * sen(30°) = 49.05 N * 0.5 = 24.525 N
Fg, perpendicular = 49.05 N * cos(30°) = 49.05 N * 0.866 = 42.487 N
Así que tenemos que la fuerza que actúa paralela al plano es de 24.525 N y la que actúa perpendicular es de 42.487 N. ¡Listo! Ahora sabemos cómo se comporta nuestro bloque en el plano inclinado.
Ejemplo Práctico 2: Movimiento en el Plano Inclinado
Ahora que sabemos calcular las fuerzas, ¿qué pasa si queremos saber la aceleración del bloque? Para esto, aplicamos la segunda ley de Newton: F = m * a.
La fuerza neta que actúa sobre el bloque es la componente paralela que hemos calculado, menos cualquier fricción que pueda existir. Supongamos que la fricción es despreciable por ahora.
Entonces, F = Fg, paralelo = 24.525 N.
Aplicamos la fórmula:
a = F/m = 24.525 N / 5 kg = 4.905 m/s².
¡Así que nuestro bloque acelerará hacia abajo a 4.905 m/s²! ¿Te imaginas cómo se sentiría si estuvieras sobre él?
¿Qué pasa con la Fricción?
La fricción es un factor importante que a menudo se pasa por alto. Cuando un objeto se mueve sobre una superficie, siempre hay una fuerza de fricción que se opone a su movimiento. En el caso de nuestro bloque en el plano inclinado, podemos incluir la fricción en nuestros cálculos.
Cálculo de la Fuerza de Fricción
La fuerza de fricción se calcula con la fórmula:
Ff = μ * Fg, perpendicular
Donde μ es el coeficiente de fricción entre el bloque y el plano. Supongamos que μ = 0.2. Entonces:
Ff = 0.2 * 42.487 N = 8.4974 N.
Ahora, la fuerza neta sería:
Fnet = Fg, paralelo – Ff = 24.525 N – 8.4974 N = 16.0276 N.
Y, usando esta fuerza neta, podemos calcular la nueva aceleración:
a = Fnet / m = 16.0276 N / 5 kg = 3.20552 m/s².
Ejemplo Práctico 3: Altura y Longitud del Plano Inclinado
Supongamos que queremos calcular la longitud del plano inclinado. Si sabemos que el bloque sube hasta una altura de 2 metros, ¿cómo lo hacemos? Aquí es donde entra en juego la trigonometría.
La relación entre la altura (h), la longitud del plano (L) y el ángulo (θ) es:
h = L * sen(θ)
Despejando L tenemos:
L = h / sen(θ).
Si θ es 30 grados y h es 2 metros, entonces:
L = 2 m / sen(30°) = 2 m / 0.5 = 4 m.
¡Y ahí lo tienes! La longitud del plano inclinado es de 4 metros.
Aplicaciones del Plano Inclinado en la Vida Real
Ahora que hemos cubierto algunos ejemplos prácticos, es interesante pensar en cómo se aplica el concepto de plano inclinado en la vida real. Desde rampas en edificios hasta el diseño de carreteras, los planos inclinados son fundamentales. ¿Te has preguntado alguna vez cómo las montañas rusas utilizan estos principios? La inclinación de las vías permite que los carros se deslicen hacia abajo gracias a la gravedad, ¡y eso es pura física en acción!
Los planos inclinados son un tema fascinante que combina matemáticas y física de una manera muy práctica. Ya sea que estés calculando fuerzas, aceleraciones o longitudes, cada ejercicio te acerca más a comprender cómo funciona el mundo a tu alrededor. Recuerda, cada vez que veas una rampa, una colina o incluso una pendiente en la carretera, estás viendo un plano inclinado en acción.
¿Qué es la fricción y cómo afecta el movimiento en un plano inclinado?
La fricción es una fuerza que se opone al movimiento. En un plano inclinado, la fricción puede reducir la aceleración del objeto que se desliza, haciendo que se necesite más fuerza para moverlo.
¿Puedo aplicar los mismos principios a un plano inclinado curvado?
¡Sí! Aunque los cálculos pueden ser un poco más complejos, los principios de descomposición de fuerzas siguen siendo aplicables. Simplemente tendrás que considerar la curvatura al calcular las fuerzas.
¿Qué pasa si el ángulo del plano inclinado es mayor a 90 grados?
Un ángulo mayor a 90 grados no se consideraría un plano inclinado en el sentido tradicional. En cambio, sería como un plano vertical, donde la gravedad tendría un efecto completamente diferente sobre el objeto.
¿Cómo puedo practicar más problemas de planos inclinados?
La mejor manera de practicar es buscar ejercicios en libros de texto de física o en línea. También puedes intentar crear tus propios problemas basados en situaciones cotidianas.
¿Los planos inclinados se utilizan en la ingeniería?
¡Absolutamente! Los ingenieros utilizan los principios de los planos inclinados en una variedad de aplicaciones, desde el diseño de rampas accesibles hasta la construcción de puentes y carreteras.
Espero que este artículo te haya proporcionado una comprensión clara y práctica de los planos inclinados. Si tienes más preguntas o necesitas aclaraciones, ¡no dudes en preguntar!