¡Hola, amigo matemático! Si estás aquí, es porque quieres adentrarte en el fascinante mundo de los números racionales. ¿Te suena familiar eso de que un número racional es aquel que puede expresarse como el cociente de dos enteros? ¡Exacto! Pero, más allá de la teoría, hoy vamos a poner las manos en la masa. Vamos a explorar ejercicios prácticos que no solo te ayudarán a entender mejor este concepto, sino que también te prepararán para enfrentar cualquier examen de 3º de ESO. Así que, si tienes un lápiz y papel a mano, ¡comencemos!
¿Qué son los Números Racionales?
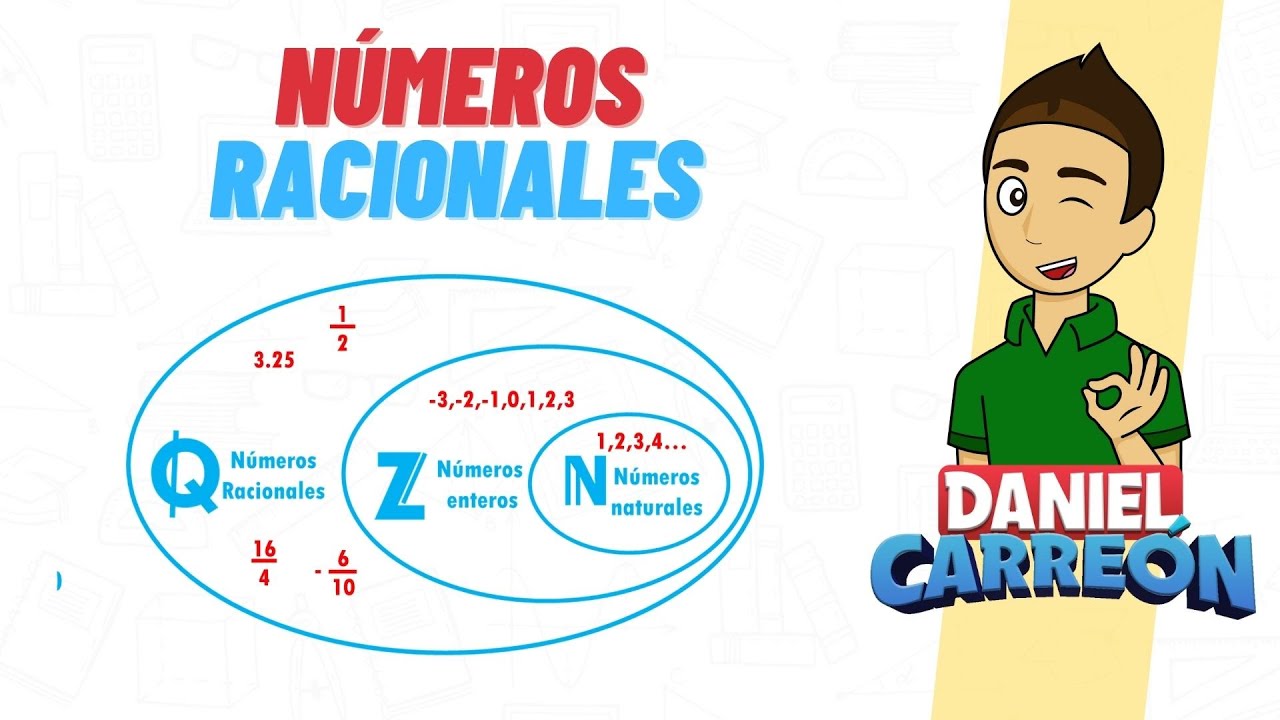
Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, donde el denominador no puede ser cero. En otras palabras, cualquier número que puedas escribir en la forma a/b, donde a y b son enteros y b ≠ 0, es un número racional. Piensa en ellos como los «números amigables» que se pueden dividir y compartir sin dejar residuos. Por ejemplo, 1/2, 3/4 y -5/2 son todos números racionales. Ahora, ¿no es emocionante pensar que los números racionales están por todas partes, desde las recetas de cocina hasta las finanzas?
Ejercicio 1: Identificación de Números Racionales
Vamos a empezar con un ejercicio sencillo. Te daré una lista de números y tú tendrás que identificar cuáles son racionales:
- 3
- √2
- -4/7
- π
- 0.75
Ahora, piensa un momento. ¿Cuáles de ellos puedes escribir como el cociente de dos enteros? ¡Correcto! Los números racionales de la lista son 3 (puedes escribirlo como 3/1), -4/7 y 0.75 (que es lo mismo que 3/4). ¡Bien hecho!
Ejercicio 2: Suma de Números Racionales
Pasemos a algo un poco más desafiante. Imagina que tienes que sumar los siguientes números racionales:
- 1/3 + 1/6
- 2/5 + 3/10
Para resolver esto, primero necesitas encontrar un denominador común. Para el primer ejercicio, el mínimo común múltiplo de 3 y 6 es 6. Así que, reescribimos 1/3 como 2/6 y luego sumamos:
2/6 + 1/6 = 3/6, que se simplifica a 1/2.
Para el segundo, el mínimo común múltiplo de 5 y 10 es 10. Entonces, 2/5 se convierte en 4/10:
4/10 + 3/10 = 7/10.
La Resta de Números Racionales
Ejercicio 3: Resta de Números Racionales
Ahora, veamos cómo restar números racionales. Aquí tienes un par de ejercicios:
- 5/8 – 1/4
- 3/5 – 2/10
Para el primero, necesitas un denominador común. El mínimo común múltiplo de 8 y 4 es 8. Entonces, reescribimos 1/4 como 2/8:
5/8 – 2/8 = 3/8.
Para el segundo ejercicio, el mínimo común múltiplo de 5 y 10 es 10. Reescribimos 3/5 como 6/10:
6/10 – 2/10 = 4/10, que se simplifica a 2/5.
Multiplicación de Números Racionales
Ejercicio 4: Multiplicación de Números Racionales
¡Es hora de multiplicar! Aquí tienes dos ejercicios para practicar:
- (2/3) * (3/4)
- (-1/2) * (4/5)
Para el primero, simplemente multiplicas los numeradores y los denominadores:
(2 * 3) / (3 * 4) = 6/12, que se simplifica a 1/2.
En el segundo caso, también multiplicamos:
(-1 * 4) / (2 * 5) = -4/10, que se simplifica a -2/5.
División de Números Racionales
Ejercicio 5: División de Números Racionales
Finalmente, llegamos a la división. Para dividir números racionales, multiplicamos por el recíproco. Prueba con estos ejemplos:
- (3/5) ÷ (2/3)
- (-4/7) ÷ (1/2)
Para el primero, multiplicamos 3/5 por el recíproco de 2/3, que es 3/2:
(3/5) * (3/2) = 9/10.
En el segundo caso:
(-4/7) * (2/1) = -8/7.
Resolviendo Problemas con Números Racionales
Ahora que ya hemos cubierto las operaciones básicas, ¿qué tal si aplicamos estos conocimientos a algunos problemas más complejos? Aquí van algunos ejercicios para que pienses un poco más.
Ejercicio 6: Problemas de Aplicación
1. Si un coche consume 3/4 de litro de gasolina por cada 10 km, ¿cuántos litros necesitará para recorrer 50 km?
2. En una clase, 2/3 de los estudiantes aprobaron matemáticas. Si hay 24 estudiantes en total, ¿cuántos aprobaron?
Para el primer problema, primero averiguamos cuántos litros se consumen por kilómetro:
(3/4) / 10 = 3/40 litros por km.
Para 50 km: 50 * (3/40) = 3.75 litros.
Para el segundo problema, calculamos:
(2/3) * 24 = 16 estudiantes aprobaron.
¡Felicidades! Has llegado al final de este recorrido por los números racionales. Has practicado identificación, suma, resta, multiplicación y división de números racionales. Ahora, cuando te encuentres con estos números en tu vida diaria, ya no te parecerán tan intimidantes. Recuerda siempre la importancia de encontrar denominadores comunes y simplificar cuando sea necesario. Con práctica y paciencia, te volverás un experto en el manejo de números racionales.
¿Qué es un número racional y cómo se diferencia de un número irracional?
Un número racional es aquel que puede expresarse como el cociente de dos enteros. Por otro lado, los números irracionales no pueden ser expresados de esta manera, como √2 o π.
¿Cómo puedo saber si un número decimal es racional?
Un número decimal es racional si se puede expresar como una fracción, lo que significa que debe ser finito o periódico. Por ejemplo, 0.75 es racional, mientras que 0.333… también lo es porque es periódico.
¿Dónde se utilizan los números racionales en la vida diaria?
Los números racionales se utilizan en muchas áreas, como la cocina (medidas), las finanzas (presupuestos), y en la ciencia (cálculos). Siempre que se trata de dividir o compartir, ¡estás usando números racionales!
¿Es posible realizar operaciones con números racionales y enteros?
¡Claro que sí! Puedes realizar operaciones con números racionales y enteros. Solo recuerda que puedes convertir el entero a una fracción (por ejemplo, 5 se convierte en 5/1) y luego realizar la operación.
¿Cuál es la clave para resolver problemas con números racionales?
La clave está en practicar y familiarizarte con las operaciones. Asegúrate de entender cómo encontrar denominadores comunes y simplificar tus respuestas. Con el tiempo, te volverás más rápido y eficiente en la resolución de problemas.
Espero que este artículo sea útil y claro para quienes buscan entender mejor los números racionales. ¡A practicar se ha dicho!