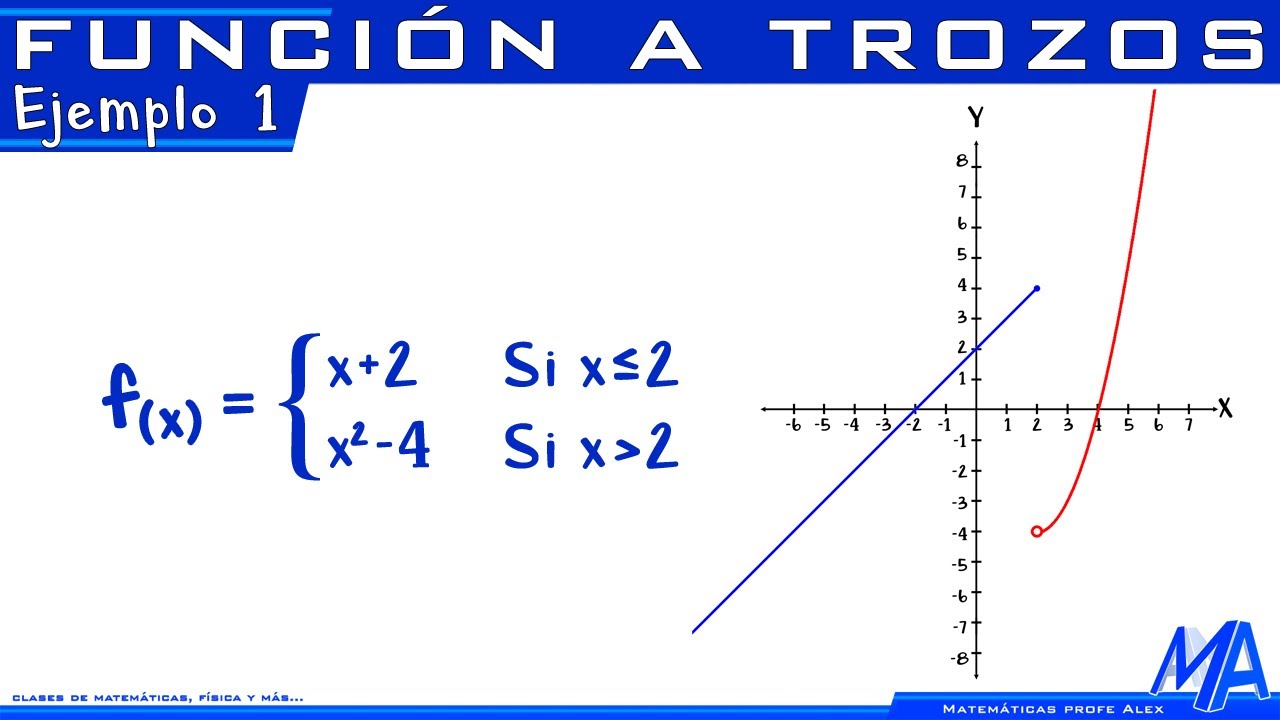
¿Qué Son las Funciones a Trozos y Por Qué Son Importantes?
Las funciones a trozos son una forma de describir funciones que cambian su comportamiento dependiendo del valor de la variable independiente. Imagínate que estás conduciendo por una carretera que tiene diferentes límites de velocidad según la zona. En la ciudad, debes ir más despacio, mientras que en la autopista puedes acelerar. Así funcionan las funciones a trozos: en diferentes intervalos de su dominio, tienen diferentes «reglas». Esta idea puede parecer un poco confusa al principio, pero con ejemplos y ejercicios prácticos, verás que es más sencilla de lo que parece. En este artículo, exploraremos qué son las funciones a trozos, cómo se construyen, y te ofreceremos ejemplos prácticos para que puedas aprender y practicar por tu cuenta.
Definiendo Funciones a Trozos
Para comenzar, definamos más claramente qué es una función a trozos. Una función a trozos se expresa en diferentes partes, cada una de las cuales se aplica a un intervalo específico del dominio. Por ejemplo, podríamos tener una función que se comporta de una manera cuando x es menor que 0, y de otra manera cuando x es mayor o igual a 0. Esto se puede escribir matemáticamente como:
f(x) = {
x + 2, si x < 0
x^2, si x ≥ 0
}
En este caso, si insertamos un valor de x que es menor que 0, utilizaremos la primera regla (x + 2), mientras que si x es igual o mayor que 0, aplicaremos la segunda regla (x^2). Este tipo de funciones son muy útiles en diversas áreas de las matemáticas y la física, donde las condiciones cambian dependiendo del contexto.
Ejemplos Prácticos de Funciones a Trozos
Ejemplo 1: Una Función Simple
Tomemos un ejemplo sencillo para entender mejor cómo funcionan estas funciones. Supongamos que tenemos la función a trozos:
f(x) = {
3x - 1, si x < 1
2, si x = 1
x^2, si x > 1
}
Ahora, analicemos cómo se comporta esta función en diferentes valores de x:
- Si x = 0, entonces f(0) = 3(0) - 1 = -1.
- Si x = 1, entonces f(1) = 2.
- Si x = 2, entonces f(2) = (2)^2 = 4.
Como puedes ver, dependiendo del valor de x, la función nos da diferentes resultados. Esto es lo que hace que las funciones a trozos sean interesantes y útiles.
Ejemplo 2: Aplicaciones en el Mundo Real
Ahora que ya hemos visto cómo funcionan, hablemos de un ejemplo del mundo real. Imagina que estás en una tienda de ropa que tiene un sistema de precios escalonados. Por ejemplo:
Precio(x) = {
10, si x < 5
8, si 5 ≤ x < 10
6, si x ≥ 10
}
En este caso, el precio de una prenda depende de cuántas compres. Si compras menos de cinco prendas, cada una cuesta 10 euros. Si compras entre cinco y diez, cada una te costará 8 euros. Y si compras diez o más, cada prenda solo costará 6 euros. Este tipo de estructura es común en descuentos por cantidad y es un gran ejemplo de cómo las funciones a trozos se aplican en la vida cotidiana.
Cómo Graficar Funciones a Trozos
Ahora que hemos visto ejemplos de funciones a trozos, es hora de aprender a graficarlas. Graficar una función a trozos puede ser un poco más complicado que graficar una función continua, pero con algunos pasos simples, puedes hacerlo sin problemas. Aquí te dejo una guía rápida:
- Identifica los puntos críticos donde la función cambia. Estos son los puntos donde las diferentes "reglas" se aplican.
- Para cada intervalo, calcula algunos puntos para tener una idea de cómo se comporta la función en ese tramo.
- Conecta los puntos con líneas. Asegúrate de usar líneas discontinuas si la función no está definida en un punto específico.
Por ejemplo, si graficamos la función que discutimos anteriormente, verás que en el intervalo x < 1, la gráfica será una línea recta, mientras que en x ≥ 1, será una parábola. Así, obtendremos una gráfica que muestra claramente cómo la función cambia de comportamiento.
Ejercicios para Practicar
Ahora que tienes una buena comprensión de las funciones a trozos, es momento de poner a prueba tus conocimientos. Aquí te dejo algunos ejercicios para que practiques:
Ejercicio 1
Define la siguiente función a trozos y calcula f(-2), f(0) y f(3):
g(x) = {
-x, si x < 0
1, si x = 0
x^3, si x > 0
}
Ejercicio 2
Imagina que estás en una heladería donde los precios son:
Precio(kg) = {
5, si kg < 1
4, si 1 ≤ kg < 5
3, si kg ≥ 5
}
¿Cuánto pagarías por 3 kg de helado? ¿Y por 6 kg?
Soluciones a los Ejercicios
Después de haber practicado, aquí tienes las soluciones para que puedas verificar tus respuestas:
Solución Ejercicio 1
Para g(-2), usamos la primera regla: g(-2) = -(-2) = 2. Para g(0), usamos la segunda regla: g(0) = 1. Para g(3), usamos la tercera regla: g(3) = (3)^3 = 27.
Solución Ejercicio 2
Para 3 kg, usamos la segunda regla: Precio(3) = 4 euros por kg, así que pagarías 12 euros. Para 6 kg, usamos la tercera regla: Precio(6) = 3 euros por kg, así que pagarías 18 euros.
Las funciones a trozos son una herramienta poderosa en matemáticas y tienen aplicaciones prácticas en muchos campos. Desde la economía hasta la ingeniería, entender cómo funcionan puede ayudarte a resolver problemas complejos de manera más efectiva. Además, practicar con ejercicios te permitirá familiarizarte más con este concepto y aplicar lo aprendido en situaciones del mundo real. Así que, ¡no dudes en seguir practicando y explorando este fascinante tema!
¿Las funciones a trozos son continuas?
Las funciones a trozos pueden ser continuas o discontinuas, dependiendo de cómo estén definidas. Por ejemplo, si hay un "salto" en los valores de la función en un punto, se considera discontinua.
¿Cómo se derivan las funciones a trozos?
Para derivar funciones a trozos, debes derivar cada parte de la función en su intervalo correspondiente. Sin embargo, debes tener cuidado con los puntos donde la función cambia, ya que pueden ser puntos de discontinuidad.
¿Dónde se utilizan las funciones a trozos en la vida real?
Las funciones a trozos se utilizan en diversas áreas, como en precios escalonados, tarifas de servicios públicos, y modelos económicos, entre otros. Son una manera efectiva de representar situaciones donde las condiciones cambian.