¡Hola! ¿Alguna vez te has preguntado cómo representar visualmente datos o problemas matemáticos? Aquí es donde entra en juego el plano cartesiano. Imagínate un mapa donde cada punto tiene una dirección específica. En este caso, el plano cartesiano actúa como ese mapa, donde podemos ubicar puntos usando coordenadas. Si bien al principio puede parecer un poco complicado, en realidad, ¡es más fácil de lo que piensas! A través de este artículo, vamos a explorar el plano cartesiano, aprenderemos a graficar puntos y resolver ejercicios prácticos que te ayudarán a comprender mejor este concepto. Así que, ¡prepárate para sumergirte en el mundo de las coordenadas!
¿Qué es el Plano Cartesiano?
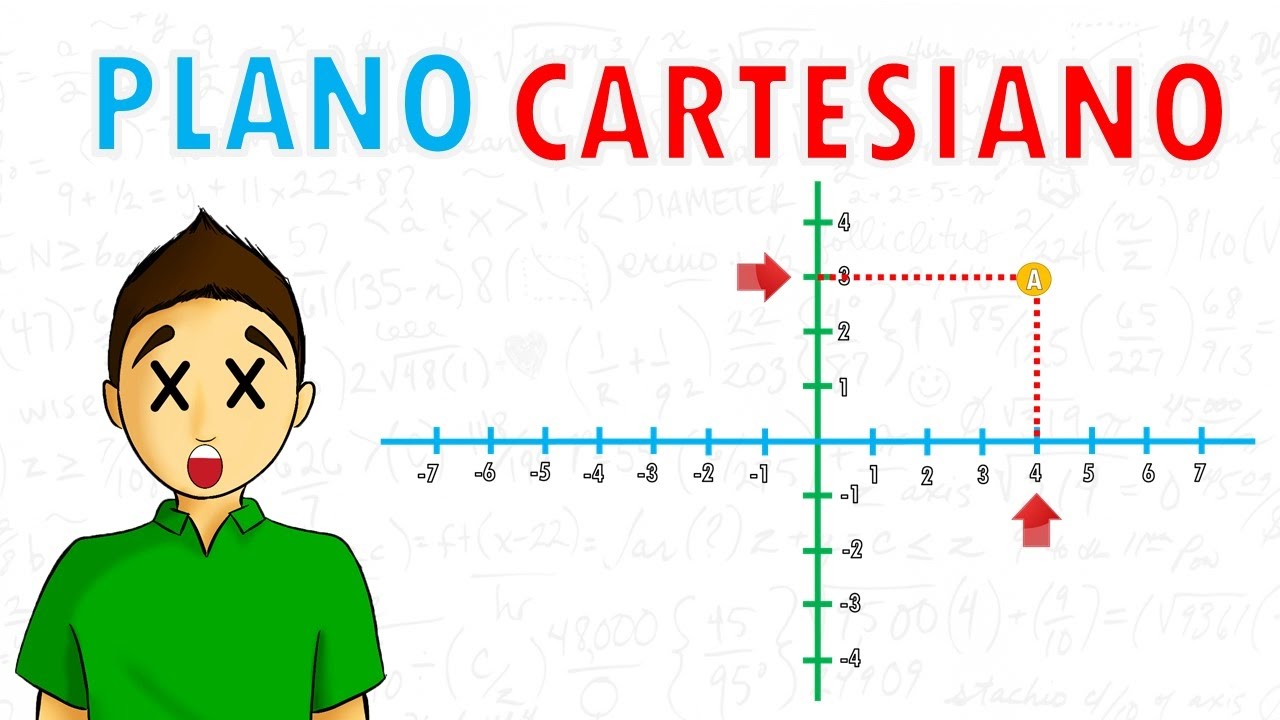
El plano cartesiano es un sistema de referencia bidimensional que se utiliza para representar puntos en un espacio definido. Se compone de dos ejes perpendiculares: el eje horizontal (eje X) y el eje vertical (eje Y). El punto donde se cruzan ambos ejes se llama origen y tiene coordenadas (0, 0). Cada punto en el plano cartesiano se identifica mediante un par ordenado de números, que son las coordenadas (x, y). Pero, ¿qué significa esto en la práctica?
Las Coordenadas: Tu Guía en el Plano
Las coordenadas (x, y) te dicen exactamente dónde se encuentra un punto en el plano. La primera parte, ‘x’, indica la posición horizontal, mientras que ‘y’ indica la posición vertical. Por ejemplo, si tienes el punto (3, 2), eso significa que debes moverte 3 unidades hacia la derecha desde el origen y luego 2 unidades hacia arriba. Es como jugar a ser un explorador en un mapa, donde cada coordenada es una pista para encontrar un tesoro escondido.
Ejercicios Prácticos para Dominar el Plano Cartesiano
Ahora que tenemos una idea básica del plano cartesiano, es hora de poner manos a la obra. Vamos a realizar algunos ejercicios prácticos que te ayudarán a mejorar tu comprensión. ¡No te preocupes, no necesitas ser un genio matemático para esto!
Ejercicio 1: Graficando Puntos
Comencemos con algo sencillo: graficar puntos. Imagina que tenemos las siguientes coordenadas: (1, 3), (4, 1) y (2, 5). Toma un papel y un lápiz, o si prefieres, puedes usar una hoja de cuadrícula. Marca los ejes X e Y y empieza a ubicar los puntos:
- Para (1, 3): Mueve 1 unidad a la derecha y 3 unidades hacia arriba.
- Para (4, 1): Mueve 4 unidades a la derecha y 1 unidad hacia arriba.
- Para (2, 5): Mueve 2 unidades a la derecha y 5 unidades hacia arriba.
¿Ves cómo cada punto se encuentra en un lugar único? ¡Genial! Ahora que tienes tus puntos en el papel, intenta conectarlos. Esto te dará una mejor idea de cómo se relacionan entre sí.
Ejercicio 2: Identificando Cuadrantes
El plano cartesiano se divide en cuatro cuadrantes, y cada uno tiene características particulares. ¿Te atreves a identificarlos? Aquí tienes un pequeño resumen:
- Cuadrante I: Ambos valores son positivos (x, y).
- Cuadrante II: x es negativo y y es positivo (-x, y).
- Cuadrante III: Ambos valores son negativos (-x, -y).
- Cuadrante IV: x es positivo y y es negativo (x, -y).
Intenta clasificar los siguientes puntos en sus respectivos cuadrantes: (3, 2), (-1, 4), (-3, -5) y (2, -3). ¿Te das cuenta de cómo la ubicación de un punto en el plano determina su cuadrante?
Aplicaciones del Plano Cartesiano en la Vida Real
Ahora que hemos practicado un poco, es interesante pensar en cómo usamos el plano cartesiano en nuestra vida diaria. ¿Alguna vez has jugado un videojuego que involucra mapas? ¡Exacto! Los videojuegos utilizan coordenadas para ubicar personajes, objetos y enemigos. Además, el diseño gráfico y la arquitectura también dependen del plano cartesiano para crear planos y diseños precisos.
El Arte de Graficar Funciones
Una de las aplicaciones más fascinantes del plano cartesiano es graficar funciones matemáticas. ¿Te imaginas cómo sería representar la relación entre la distancia y el tiempo en un gráfico? Puedes ver cómo cambia la distancia a medida que pasa el tiempo. Por ejemplo, si tienes la función lineal y = 2x + 1, puedes graficar puntos y ver cómo la línea se eleva a medida que x aumenta. Es como observar una historia contada a través de un gráfico.
Desafiando tu Comprensión: Problemas Interesantes
Ahora que te sientes más cómodo con el plano cartesiano, vamos a desafiarte con algunos problemas interesantes. ¡No te preocupes si no lo resuelves de inmediato, la práctica hace al maestro!
Problema 1: Encuentra la Distancia entre dos Puntos
Supongamos que tienes los puntos A(2, 3) y B(5, 7). ¿Cómo puedes encontrar la distancia entre ellos? Aquí entra en juego la fórmula de la distancia:
D = √((x2 – x1)² + (y2 – y1)²)
Utiliza la fórmula y descubre la distancia entre A y B. ¡Te sorprenderá cuánto puedes aprender simplemente aplicando una fórmula!
Problema 2: El Camino Más Corto
Imagina que estás tratando de encontrar el camino más corto entre dos puntos en el plano cartesiano. ¿Cómo lo harías? Puedes utilizar el mismo método que en el problema anterior, pero esta vez piensa en cómo podrías graficar el camino más corto. ¡Es como un juego de estrategia donde debes encontrar la mejor ruta!
1. ¿Es necesario saber álgebra para entender el plano cartesiano?
No necesariamente. Aunque el álgebra puede ayudarte a graficar funciones y resolver problemas más complejos, puedes comenzar a comprender el plano cartesiano solo con coordenadas y puntos.
2. ¿Cómo puedo practicar más sobre el plano cartesiano?
Puedes usar aplicaciones en línea, libros de ejercicios o incluso crear tus propios problemas y graficarlos. La práctica constante te ayudará a sentirte más cómodo.
3. ¿El plano cartesiano solo se utiliza en matemáticas?
No, se utiliza en muchas disciplinas, como la física, la ingeniería, el arte y la economía. ¡Es una herramienta versátil!
4. ¿Qué pasa si mis coordenadas son negativas?
Las coordenadas negativas simplemente indican que el punto está en el lado opuesto del origen. No te preocupes, ¡siguen siendo parte del plano cartesiano!
5. ¿Cómo puedo recordar en qué cuadrante se encuentra un punto?
Una buena manera de recordarlo es pensar en la posición de los signos. Cuadrante I es positivo, II es negativo en x y positivo en y, III es negativo en ambos y IV es positivo en x y negativo en y. ¡Hazlo un juego!
Espero que este artículo te haya ayudado a comprender mejor el plano cartesiano. Recuerda que la práctica es clave, así que no dudes en seguir explorando y experimentando con tus propias coordenadas. ¡Diviértete graficando!