¡Hola, estudiantes de física! Hoy vamos a sumergirnos en el fascinante mundo de los planos inclinados. Si alguna vez has visto una rampa y te has preguntado cómo se relacionan la gravedad, la fricción y el movimiento, este artículo es para ti. Los planos inclinados son una de esas maravillas de la física que, aunque parecen simples, tienen un trasfondo muy interesante. Imagina que estás en un parque de atracciones y decides probar una montaña rusa. ¿Alguna vez pensaste en cómo esa inclinación afecta tu velocidad y la fuerza que sientes? Vamos a desglosar todo esto y más, así que prepárate para un viaje emocionante a través de la física.
¿Qué es un Plano Inclinado?
Un plano inclinado es, en términos simples, una superficie que está inclinada respecto a la horizontal. Piensa en una rampa: es un ejemplo clásico. En la física, utilizamos planos inclinados para analizar cómo las fuerzas afectan el movimiento de los objetos. La clave aquí es que la gravedad no actúa de la misma manera en un plano inclinado como lo hace en una superficie plana. Así que, ¿qué sucede cuando colocas un objeto en una rampa? La gravedad comienza a hacer su magia.
Descomposición de Fuerzas
Cuando un objeto está en un plano inclinado, la fuerza de gravedad se puede descomponer en dos componentes: uno que actúa perpendicular al plano y otro que actúa a lo largo del plano. ¿Te suena complicado? No te preocupes, es más fácil de lo que parece. Imagina que tienes una caja sobre una rampa. La fuerza de gravedad (que siempre actúa hacia abajo) se puede dividir en dos: una que empuja la caja hacia el plano y otra que intenta hacerla deslizar hacia abajo. Esto es crucial para entender cómo se mueven los objetos en estas superficies.
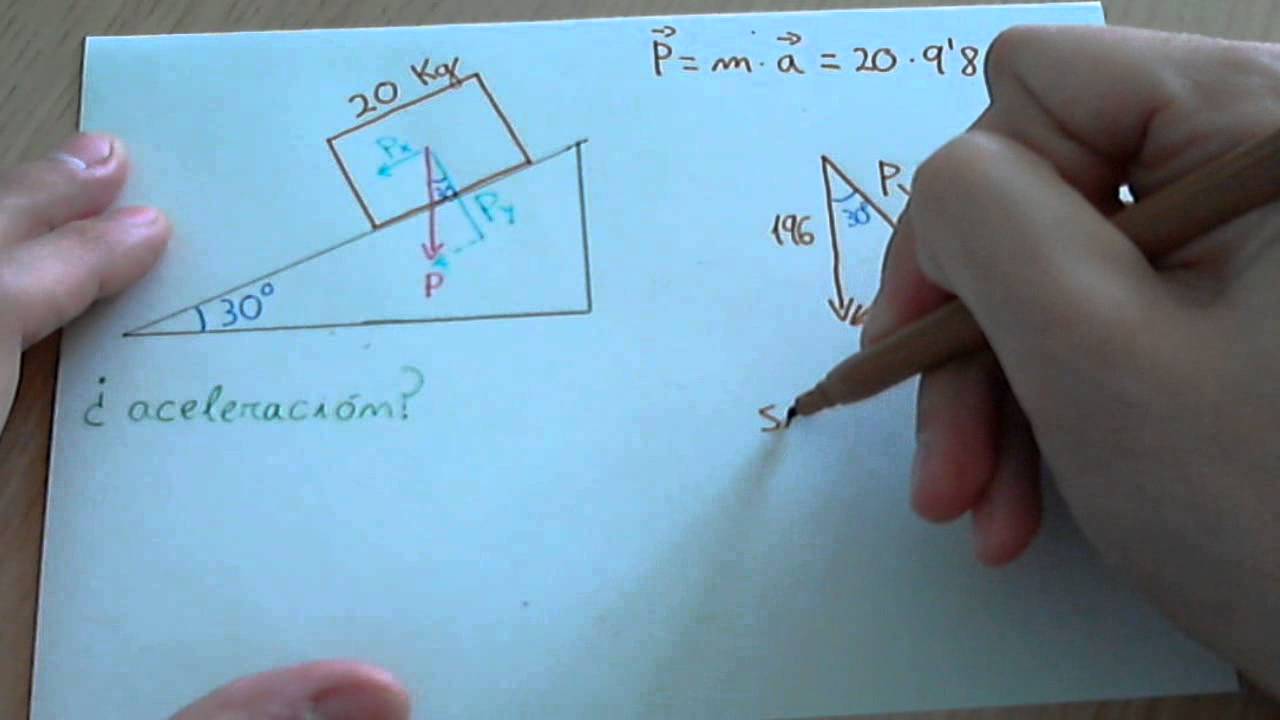
Ejemplo Práctico: Un Bloque en una Rampa
Vamos a ver un ejercicio práctico. Imagina que tienes un bloque de 10 kg en una rampa que tiene un ángulo de inclinación de 30 grados. Queremos saber cómo se comporta este bloque. Primero, necesitamos calcular las fuerzas que actúan sobre él. La fuerza de gravedad es simplemente el peso del bloque, que se calcula como:
Fuerza de gravedad (Fg) = masa (m) × gravedad (g)
Donde la gravedad en la Tierra es aproximadamente 9.81 m/s². Entonces:
Fg = 10 kg × 9.81 m/s² = 98.1 N
Ahora, descomponemos esta fuerza en sus componentes. La fuerza que actúa a lo largo del plano (Fparallel) se calcula usando el seno del ángulo de inclinación:
Fparallel = Fg × sen(θ)
Así que:
Fparallel = 98.1 N × sen(30°) = 98.1 N × 0.5 = 49.05 N
Esto significa que el bloque experimenta una fuerza de 49.05 N que lo empuja hacia abajo por la rampa. Pero, ¿qué pasa con la fricción? Ah, eso es otro aspecto importante que no podemos ignorar.
El Papel de la Fricción
La fricción es la resistencia que enfrenta un objeto cuando se mueve sobre una superficie. En nuestro ejemplo, si la rampa está hecha de madera, la fricción será diferente que si estuviera hecha de metal. Para calcular la fuerza de fricción, utilizamos la fórmula:
Fricción (Ff) = coeficiente de fricción (μ) × fuerza normal (N)
La fuerza normal es la fuerza que actúa perpendicularmente al plano. En este caso, es igual a la componente de la fuerza de gravedad que actúa perpendicularmente al plano, que se calcula como:
N = Fg × cos(θ)
Entonces:
N = 98.1 N × cos(30°) = 98.1 N × 0.866 = 85.23 N
Ahora, si asumimos que el coeficiente de fricción entre el bloque y la rampa es 0.3, podemos calcular la fuerza de fricción:
Ff = 0.3 × 85.23 N = 25.57 N
Así que ahora tenemos la fuerza que empuja el bloque hacia abajo y la fuerza de fricción que lo detiene. ¡Hora de calcular la aceleración!
Cálculo de la Aceleración
Para encontrar la aceleración del bloque, aplicamos la segunda ley de Newton, que nos dice que la fuerza neta es igual a la masa multiplicada por la aceleración (F = ma). La fuerza neta (Fnet) es la fuerza que actúa a lo largo del plano menos la fuerza de fricción:
Fnet = Fparallel – Ff
Así que:
Fnet = 49.05 N – 25.57 N = 23.48 N
Ahora, usando la segunda ley de Newton:
23.48 N = 10 kg × a
Despejamos para encontrar la aceleración (a):
a = 23.48 N / 10 kg = 2.348 m/s²
Y ahí lo tienes. La aceleración del bloque mientras se desliza por la rampa es de 2.348 m/s². Esto es solo un vistazo a lo que los planos inclinados pueden enseñarnos sobre el movimiento y las fuerzas. Pero, ¿qué tal si profundizamos un poco más?
Aplicaciones Prácticas de los Planos Inclinados
Los planos inclinados no son solo un concepto académico; tienen aplicaciones en la vida real. Desde rampas de acceso para personas con discapacidad hasta montañas rusas y grúas, este principio de la física está en todas partes. ¿Alguna vez te has preguntado cómo los edificios son construidos en terrenos inclinados? Los ingenieros utilizan planos inclinados para calcular la estabilidad y la seguridad de las estructuras. Así que, la próxima vez que veas una rampa o una montaña rusa, piensa en la física que hay detrás.
Ejercicios Adicionales
Para que puedas practicar y dominar este tema, aquí tienes algunos ejercicios adicionales que puedes intentar:
- Un objeto de 5 kg se desliza por una rampa de 45 grados. ¿Cuál es su aceleración si el coeficiente de fricción es 0.2?
- Un bloque de 8 kg está en una rampa de 60 grados. ¿Qué fuerza se necesita para mantenerlo en reposo si el coeficiente de fricción es 0.4?
- Calcula la velocidad de un objeto que baja por una rampa de 30 grados durante 3 segundos. Suponiendo que no hay fricción.
¡Anímate a resolver estos problemas y mejora tu comprensión sobre los planos inclinados!
Los planos inclinados son un tema esencial en la física que nos ayuda a entender cómo las fuerzas interactúan con los objetos. Desde la descomposición de fuerzas hasta el impacto de la fricción, cada aspecto es crucial para resolver problemas del mundo real. Ahora que tienes una mejor comprensión, ¿por qué no aplicas estos conceptos en tu próxima clase de física? ¡Seguro que sorprenderás a tu profesor!
- ¿Qué es un plano inclinado en términos simples? Es una superficie que está inclinada respecto a la horizontal y se utiliza para analizar el movimiento de objetos.
- ¿Cómo afecta la fricción a un objeto en un plano inclinado? La fricción actúa como una resistencia que puede ralentizar o detener el movimiento del objeto.
- ¿Por qué es importante descomponer fuerzas en un plano inclinado? Descomponer fuerzas nos ayuda a entender cómo actúan diferentes componentes de la gravedad sobre el objeto.
- ¿Puedo encontrar planos inclinados en la vida cotidiana? Sí, los vemos en rampas, montañas rusas, y en la construcción de edificios en terrenos inclinados.
- ¿Cómo se relacionan los planos inclinados con la energía? Los planos inclinados pueden influir en la energía potencial y cinética de un objeto, afectando su velocidad y movimiento.