Aprendiendo Funciones Lineales de Forma Divertida
¡Hola, estudiantes de 2º de ESO! Hoy nos adentraremos en el fascinante mundo de las funciones lineales. Quizás pienses que las matemáticas son aburridas, pero te prometo que, con los ejercicios que vamos a ver, te sorprenderás de lo divertidas que pueden ser. Las funciones lineales son como el GPS de las matemáticas: nos ayudan a trazar caminos y a entender cómo cambian las cosas en el mundo que nos rodea. ¿Listos para descubrirlo? Vamos a ello.
¿Qué es una Función Lineal?
Primero, hablemos de qué es exactamente una función lineal. En términos simples, una función lineal es una relación matemática entre dos variables que se representa con una línea recta en un gráfico. Su forma más común es y = mx + b, donde m es la pendiente de la línea y b es la intersección con el eje y. ¿Te imaginas que cada vez que subes una colina, la pendiente te dice cuán empinada es? Eso es lo que hace m por nosotros. Por otro lado, b es como el punto de partida de tu aventura. ¡Vamos a explorar cómo funcionan!
Ejercicio 1: Encontrar la Pendiente
Supongamos que tenemos dos puntos: (2, 3) y (4, 7). Para encontrar la pendiente m, usamos la fórmula:
m = (y2 – y1) / (x2 – x1)
Ahora, sustituyamos los valores:
m = (7 – 3) / (4 – 2) = 4 / 2 = 2
Entonces, la pendiente de nuestra línea es 2. Esto significa que por cada unidad que avanzamos en el eje x, subimos 2 unidades en el eje y. ¡Genial!
Solución del Ejercicio 1
Así que, si tienes dos puntos en el plano, recuerda: ¡la pendiente es tu mejor amiga! Te ayuda a entender cómo se relacionan esos puntos entre sí.
Ejercicio 2: Ecuación de la Recta
Ahora que tenemos la pendiente, vamos a encontrar la ecuación de la recta que pasa por esos puntos. Usamos la forma punto-pendiente de la ecuación de la recta:
y – y1 = m(x – x1)
Eligiendo el punto (2, 3), sustituimos:
y – 3 = 2(x – 2)
Desarrollando la ecuación:
y – 3 = 2x – 4
Sumando 3 a ambos lados:
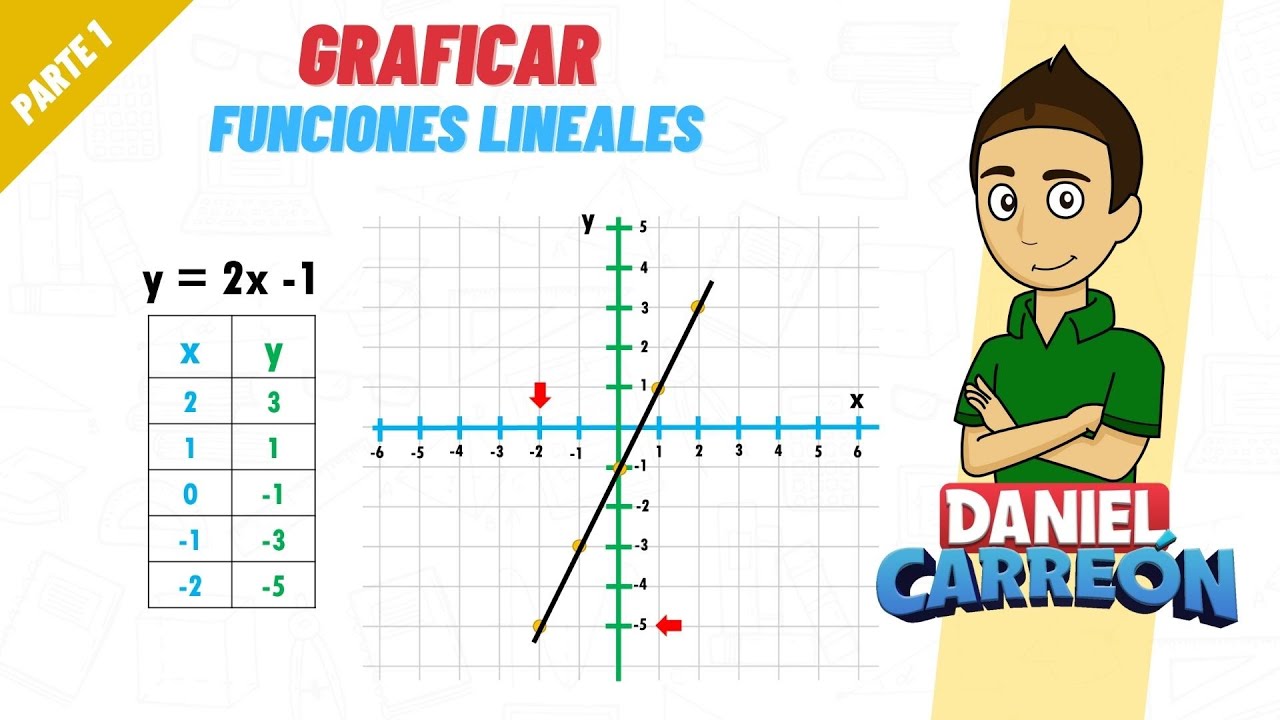
y = 2x – 1
Solución del Ejercicio 2
Así que, la ecuación de nuestra recta es y = 2x – 1. ¡Fácil, ¿verdad? Ahora ya tienes una herramienta para predecir valores!
Ejercicio 3: Gráfica de la Función Lineal
Vamos a graficar la función que acabamos de encontrar. La ecuación y = 2x – 1 nos dice que cuando x es 0, y es -1. Cuando x es 1, y es 1, y cuando x es 2, y es 3. Si trazamos estos puntos en un plano cartesiano, obtendremos una línea recta. ¿Ves cómo se forma? La gráfica es la representación visual de la relación entre x e y.
Solución del Ejercicio 3
Recuerda, cada punto en la gráfica es como una parada en un viaje. Te dice dónde estás y hacia dónde te diriges. ¡Es emocionante ver cómo se conecta todo!
Ejercicio 4: Intersección con el Eje Y
Ahora, ¿qué pasa si queremos encontrar la intersección de nuestra recta con el eje y? Simplemente necesitamos hacer que x sea 0 en nuestra ecuación:
y = 2(0) – 1 = -1
Esto significa que la línea cruza el eje y en el punto (0, -1). ¡Este punto es crucial porque nos ayuda a entender dónde comienza nuestra función!
Solución del Ejercicio 4
Conocer la intersección con el eje y es como saber dónde empieza una carrera. Te da un punto de referencia para todo lo que sigue.
Ejercicio 5: Intersección con el Eje X
Para encontrar la intersección con el eje x, tenemos que hacer que y sea 0:
0 = 2x – 1
Resolviendo para x:
2x = 1
x = 1/2
Así que, la intersección con el eje x es el punto (1/2, 0). ¡Eso es otro punto importante en nuestra gráfica!
Solución del Ejercicio 5
Conocer la intersección con el eje x es como encontrar el final de una ruta. Te dice hasta dónde puedes llegar en una dirección.
Ejercicio 6: Aplicaciones de las Funciones Lineales
Las funciones lineales no son solo números en una hoja de papel; se aplican en la vida real. Imagina que eres un vendedor. Si vendes un producto a un precio fijo, puedes usar una función lineal para calcular tus ingresos. Por ejemplo, si vendes cada producto a 10 euros y quieres saber cuánto ganarás al vender 5 productos, simplemente multiplicas:
Ingreso = Precio x Cantidad
Ingreso = 10 x 5 = 50 euros
Así que, las funciones lineales son herramientas poderosas para predecir y analizar situaciones cotidianas.
Solución del Ejercicio 6
Recuerda, las matemáticas están en todas partes, ¡solo hay que saber dónde mirar!
Ejercicio 7: Problemas del Mundo Real
Imagina que tienes un presupuesto para una fiesta. Si cada invitado cuesta 15 euros y tienes un presupuesto total de 150 euros, ¿cuántos invitados puedes invitar? Usamos la función lineal:
y = 15x
Donde y es el presupuesto y x es el número de invitados. Queremos que y sea igual a 150:
150 = 15x
x = 150/15 = 10
Puedes invitar a 10 amigos. ¡Listo para la fiesta!
Solución del Ejercicio 7
Las funciones lineales te ayudan a planificar y tomar decisiones. ¡Es como tener un superpoder!
1. ¿Por qué son importantes las funciones lineales?
Las funciones lineales son fundamentales porque nos ayudan a entender y predecir comportamientos en situaciones cotidianas, desde finanzas hasta física. Son la base de muchos conceptos más avanzados en matemáticas.
2. ¿Cómo puedo practicar más funciones lineales?
Puedes buscar ejercicios en línea, trabajar con libros de texto o incluso crear tus propios problemas basados en situaciones reales. ¡La práctica hace al maestro!
3. ¿Las funciones lineales aparecen en otros temas de matemáticas?
¡Definitivamente! Las funciones lineales son la base para aprender sobre funciones cuadráticas, sistemas de ecuaciones y mucho más. Son como el primer paso en una escalera hacia conceptos más complejos.
4. ¿Puedo usar funciones lineales en mi vida diaria?
Por supuesto. Desde calcular gastos hasta planificar un viaje, las funciones lineales son herramientas útiles para tomar decisiones informadas en tu día a día.
5. ¿Qué hago si no entiendo un concepto de funciones lineales?
No te preocupes, todos aprendemos a nuestro propio ritmo. Puedes pedir ayuda a tus profesores, buscar tutoriales en línea o estudiar en grupo. ¡La clave es no rendirse!
Así que ahí lo tienes, un viaje emocionante a través de las funciones lineales. Espero que ahora veas estas herramientas matemáticas de una manera diferente y más divertida. ¡Sigue practicando y nunca dejes de aprender!