¿Alguna vez te has preguntado por qué es importante conocer el área y el perímetro de las figuras geométricas? Imagina que estás en una tienda de muebles y quieres comprar una alfombra para tu habitación. Necesitas saber el tamaño del suelo, ¿verdad? Eso es precisamente lo que hacemos cuando calculamos áreas y perímetros. En este artículo, vamos a sumergirnos en el fascinante mundo de las áreas y los perímetros, y te proporcionaremos ejercicios prácticos y soluciones para que puedas dominar estos conceptos en 1º de ESO. ¡Vamos a ello!
## ¿Qué son el Área y el Perímetro?
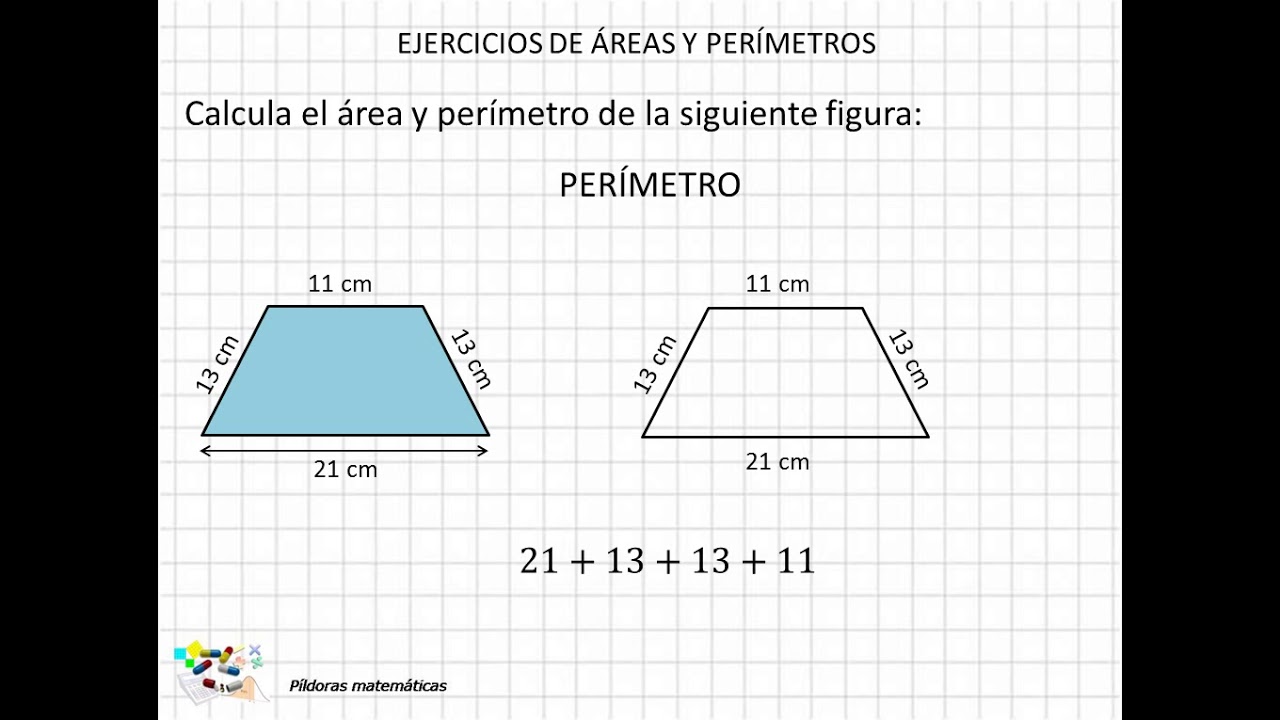
### El Perímetro
Comencemos con el perímetro. El perímetro es la distancia total alrededor de una figura. Piensa en ello como si estuvieras caminando alrededor de un parque: cada paso que das suma a la distancia total. Para calcular el perímetro de un cuadrado, simplemente sumas la longitud de todos sus lados. Por ejemplo, si cada lado mide 4 metros, el perímetro será 4 + 4 + 4 + 4, es decir, 16 metros. ¡Sencillo, verdad?
### El Área
Ahora, pasemos al área. El área es la cantidad de espacio dentro de una figura. Usando nuestra analogía del parque, si quieres saber cuánto espacio hay para jugar, eso es el área. Para un cuadrado, multiplicamos la longitud de un lado por sí mismo. Así que, si un lado mide 4 metros, el área sería 4 x 4, que equivale a 16 metros cuadrados. Aquí empieza la diversión, porque hay diferentes fórmulas para distintas figuras.
## Ejercicios Prácticos
### Ejercicio 1: Cuadrado
Problema: Calcula el área y el perímetro de un cuadrado cuyo lado mide 5 cm.
Solución:
– Perímetro: 5 + 5 + 5 + 5 = 20 cm
– Área: 5 x 5 = 25 cm²
### Ejercicio 2: Rectángulo
Problema: Un rectángulo tiene una base de 8 m y una altura de 3 m. ¿Cuál es su área y su perímetro?
Solución:
– Perímetro: 2(8 + 3) = 2(11) = 22 m
– Área: 8 x 3 = 24 m²
### Ejercicio 3: Triángulo
Problema: Un triángulo tiene una base de 6 cm y una altura de 4 cm. Calcula su área.
Solución:
– Área: (base x altura) / 2 = (6 x 4) / 2 = 12 cm²
## Profundizando en las Fórmulas
### Fórmulas para Diferentes Figuras
Conocer las fórmulas es clave. Aquí te dejo un resumen rápido:
– Cuadrado:
– Perímetro: P = 4 * lado
– Área: A = lado²
– Rectángulo:
– Perímetro: P = 2 * (base + altura)
– Área: A = base * altura
– Triángulo:
– Perímetro: P = lado1 + lado2 + lado3
– Área: A = (base * altura) / 2
– Círculo:
– Perímetro (Circunferencia): C = 2 * π * radio
– Área: A = π * radio²
### Ejercicio 4: Círculo
Problema: Un círculo tiene un radio de 3 cm. ¿Cuál es su área y circunferencia?
Solución:
– Circunferencia: C = 2 * π * 3 ≈ 18.84 cm
– Área: A = π * 3² ≈ 28.27 cm²
## Aplicaciones en la Vida Real
Ahora que ya hemos visto varios ejercicios, es importante entender cómo aplicamos esto en nuestra vida diaria. Imagina que eres un arquitecto y necesitas diseñar una casa. Debes calcular el área del terreno, la cantidad de pintura para las paredes, o incluso el espacio que ocuparán los muebles. Todo esto se reduce a entender áreas y perímetros.
### Comparación con Situaciones Cotidianas
¿Recuerdas cuando fuiste a la playa y querías poner tu toalla? Primero, tuviste que ver cuánto espacio había disponible. Esa es la misma lógica: calcular el área disponible. O piensa en cuando compras césped para tu jardín. Necesitas saber cuánto césped comprar, y eso se basa en el área del jardín. ¡Es fascinante cómo las matemáticas se entrelazan con nuestras vidas!
## Consejos para Resolver Ejercicios
1. Dibuja un Esquema: A veces, ver la figura te ayudará a entender mejor el problema.
2. Identifica las Dimensiones: Asegúrate de saber qué medidas tienes y cuáles necesitas.
3. Utiliza las Fórmulas Correctas: No todas las figuras tienen la misma fórmula, así que ten cuidado.
4. Revisa tu Trabajo: Después de calcular, siempre es bueno revisar si tus resultados tienen sentido.
## Preguntas Frecuentes
### ¿Por qué es importante aprender sobre áreas y perímetros?
Aprender sobre áreas y perímetros te ayuda a resolver problemas prácticos en la vida diaria, como planificar espacios y realizar compras adecuadas.
### ¿Qué pasa si una figura tiene lados de diferentes longitudes?
Para figuras irregulares, debes sumar la longitud de todos los lados para el perímetro y usar fórmulas específicas para el área, si están disponibles.
### ¿Las unidades de medida son importantes?
¡Absolutamente! Siempre debes incluir las unidades en tus cálculos. Por ejemplo, cm² para el área y cm para el perímetro.
### ¿Puedo usar calculadora para estos ejercicios?
Sí, puedes usar una calculadora, pero asegúrate de entender el proceso. La práctica te ayudará a mejorar tus habilidades matemáticas.
### ¿Cómo puedo mejorar en el cálculo de áreas y perímetros?
Practicar regularmente con ejercicios de diferentes niveles de dificultad te ayudará a familiarizarte con las fórmulas y a aumentar tu confianza.
Con esto, ya tienes una base sólida para entender y calcular áreas y perímetros. ¡Así que a practicar se ha dicho! Recuerda, las matemáticas son como un rompecabezas, y cada pieza que encajas te acerca más a la solución. ¡Suerte!