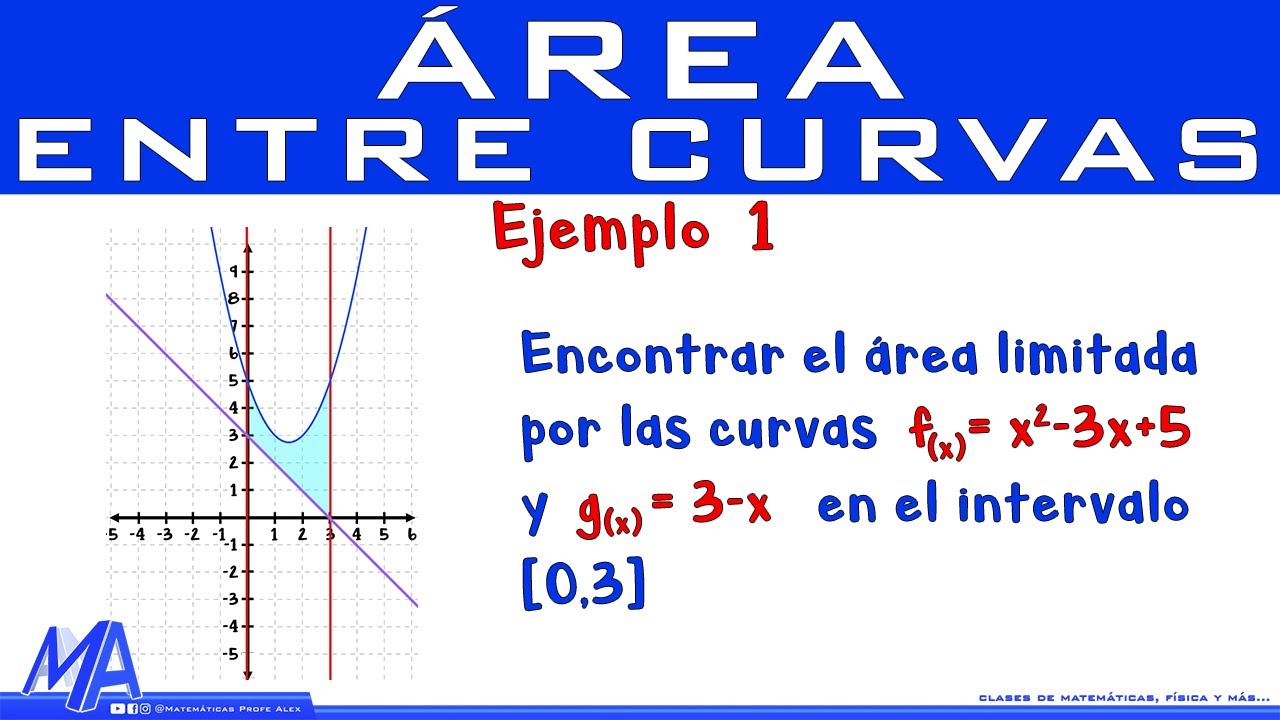
¿Alguna vez te has preguntado cómo se puede calcular el área de una figura irregular? O, más aún, ¿cómo podemos usar algo tan abstracto como las integrales para resolver problemas del mundo real? En este artículo, nos sumergiremos en el fascinante mundo del cálculo de áreas utilizando integrales. Imagina que las integrales son como una herramienta mágica que te permite descomponer formas complejas en piezas más manejables. Así como un chef corta ingredientes para preparar un delicioso platillo, nosotros también descompondremos funciones para encontrar áreas. ¿Listo para explorar? Vamos a ello.
¿Qué son las Integrales?
Las integrales son, en términos sencillos, una forma de sumar infinitas pequeñas cantidades para encontrar el total. Es como contar las gotas de agua en un estanque: cada gota es pequeña, pero al sumarlas todas, obtienes un volumen significativo. En matemáticas, la integral se utiliza para calcular áreas bajo curvas, volúmenes y mucho más. Hay dos tipos principales de integrales: las integrales definidas y las indefinidas. Las primeras te dan un número específico (como el área bajo una curva entre dos puntos), mientras que las segundas te devuelven una función. Pero hoy nos enfocaremos en las integrales definidas, que son clave para calcular áreas.
Fundamentos del Cálculo de Áreas con Integrales
El Teorema Fundamental del Cálculo
Antes de lanzarnos a los ejercicios, es crucial entender el Teorema Fundamental del Cálculo. Este teorema establece una conexión entre la derivación y la integración, y nos dice que si tienes una función continua en un intervalo cerrado, puedes calcular el área bajo la curva utilizando una integral definida. En términos simples, si tienes una función ( f(x) ) y quieres encontrar el área entre ( a ) y ( b ), se expresa así:
[ A = int_{a}^{b} f(x) , dx ]
¡Así de sencillo! Este símbolo ( int ) nos dice que estamos sumando infinitas pequeñas áreas (rectángulos) bajo la curva de ( f(x) ) entre los límites ( a ) y ( b ). Pero, ¿cómo sabemos qué función usar? Bueno, eso nos lleva a nuestro próximo tema: identificar las funciones.
Identificación de Funciones
Identificar la función que representa el área que deseas calcular es esencial. A veces, puede ser obvio, como en el caso de una parábola o una línea recta. Pero otras veces, puede ser un poco más complicado. Imagina que estás tratando de encontrar el área bajo la curva de una función que representa la trayectoria de un proyectil. Necesitarás conocer la ecuación que describe esa trayectoria. Aquí es donde entra la geometría y el conocimiento previo de funciones. Recuerda, no hay una sola forma de abordar esto, y la práctica te ayudará a mejorar.
Ejemplo Práctico 1: Área Bajo una Curva Lineal
Para poner en práctica lo que hemos aprendido, vamos a calcular el área bajo la curva de la función lineal ( f(x) = 2x + 1 ) desde ( x = 0 ) hasta ( x = 3 ).
Paso 1: Configurar la Integral
Primero, necesitamos escribir la integral definida que representa el área:
[ A = int_{0}^{3} (2x + 1) , dx ]
Paso 2: Calcular la Integral
Ahora, resolvamos la integral. Para ello, encontramos la antiderivada de ( 2x + 1 ):
[ F(x) = x^2 + x ]
Ahora evaluamos ( F(x) ) en los límites ( 0 ) y ( 3 ):
[ A = F(3) – F(0) = (3^2 + 3) – (0^2 + 0) = 9 + 3 – 0 = 12 ]
¡Y ahí lo tienes! El área bajo la curva desde ( x = 0 ) hasta ( x = 3 ) es 12 unidades cuadradas.
Ejemplo Práctico 2: Área Bajo una Curva Cuadrática
Pasemos a algo un poco más complicado. Vamos a calcular el área bajo la curva de la función cuadrática ( f(x) = x^2 ) desde ( x = 1 ) hasta ( x = 2 ).
Paso 1: Configurar la Integral
Al igual que antes, comenzamos escribiendo la integral:
[ A = int_{1}^{2} x^2 , dx ]
Paso 2: Calcular la Integral
Ahora, encontramos la antiderivada de ( x^2 ):
[ F(x) = frac{x^3}{3} ]
Evaluamos ( F(x) ) en los límites ( 1 ) y ( 2 ):
[ A = F(2) – F(1) = left(frac{2^3}{3}right) – left(frac{1^3}{3}right) = left(frac{8}{3}right) – left(frac{1}{3}right) = frac{7}{3} ]
Por lo tanto, el área bajo la curva desde ( x = 1 ) hasta ( x = 2 ) es ( frac{7}{3} ) unidades cuadradas.
Ejemplo Práctico 3: Área Entre Dos Curvas
Ahora, ¿qué sucede cuando queremos encontrar el área entre dos curvas? Imagina que tenemos las funciones ( f(x) = x^2 ) y ( g(x) = x + 2 ). Queremos encontrar el área entre estas dos curvas desde ( x = 0 ) hasta ( x = 2 ).
Paso 1: Encontrar los Puntos de Intersección
Primero, necesitamos saber dónde se cruzan las dos funciones. Igualamos las funciones:
[ x^2 = x + 2 ]
Resolviendo esta ecuación, encontramos que los puntos de intersección son ( x = -1 ) y ( x = 2 ). Sin embargo, solo consideraremos el intervalo ( [0, 2] ).
Paso 2: Configurar la Integral
El área entre las dos curvas se puede encontrar utilizando la siguiente integral:
[ A = int_{0}^{2} (g(x) – f(x)) , dx = int_{0}^{2} ((x + 2) – x^2) , dx ]
Paso 3: Calcular la Integral
Ahora resolvemos:
[ A = int_{0}^{2} (x + 2 – x^2) , dx = int_{0}^{2} (-x^2 + x + 2) , dx ]
Encontramos la antiderivada:
[ F(x) = -frac{x^3}{3} + frac{x^2}{2} + 2x ]
Ahora evaluamos:
[ A = F(2) – F(0) = left(-frac{2^3}{3} + frac{2^2}{2} + 2(2)right) – 0 ]
Calculando esto, obtenemos:
[ A = left(-frac{8}{3} + 2 + 4right) = -frac{8}{3} + 6 = -frac{8}{3} + frac{18}{3} = frac{10}{3} ]
Así que el área entre las dos curvas desde ( x = 0 ) hasta ( x = 2 ) es ( frac{10}{3} ) unidades cuadradas.
Consejos para Resolver Ejercicios de Cálculo de Áreas
Antes de concluir, aquí tienes algunos consejos prácticos para resolver ejercicios de cálculo de áreas con integrales:
- Practica con diferentes tipos de funciones: Cuanto más te expongas a diversas funciones, mejor comprenderás cómo abordarlas.
- Dibuja gráficos: Visualizar la función y el área que deseas calcular puede ayudarte a entender mejor el problema.
- Revisa tus cálculos: Los errores en la integración pueden llevar a resultados incorrectos. Siempre verifica tus pasos.
- Usa software o calculadoras: Herramientas como Wolfram Alpha pueden ayudarte a verificar tus respuestas.
¿Qué tipo de funciones puedo usar para calcular áreas con integrales?
Puedes usar cualquier función continua y acotada en el intervalo que estás considerando. Funciones lineales, cuadráticas, cúbicas y trigonométricas son algunas de las más comunes.
¿Cómo sé si debo restar dos funciones al calcular el área entre ellas?
Debes restar la función inferior de la función superior. Si ( g(x) ) está por encima de ( f(x) ) en el intervalo considerado, entonces el área se calcula como ( int (g(x) – f(x)) , dx ).
¿Puedo calcular áreas que no son geométricamente simples?
¡Absolutamente! Las integrales son extremadamente versátiles y pueden aplicarse a una amplia variedad de situaciones, incluso en contextos más abstractos.
¿Cuál es la diferencia entre una integral definida y una indefinida?
Una integral definida te da un valor numérico (como el área bajo una curva), mientras que una integral indefinida te da una función que representa una familia de antiderivadas.
¿Qué hago si me siento atascado en un problema de integración?
No te preocupes, es normal. Intenta descomponer el problema en pasos más pequeños, revisa tus notas, o busca ejemplos similares. A veces, un descanso breve también puede ayudar a aclarar tus ideas.
Así que, ¡ahí lo tienes! Hemos cubierto desde los fundamentos de las integrales hasta ejemplos prácticos de cómo calcular áreas. Espero que ahora te sientas más cómodo utilizando integrales para resolver problemas de áreas. ¡Feliz integración!