¿Por qué son importantes los ejercicios de aplicación de derivadas?
Las derivadas son una herramienta fundamental en el mundo de las matemáticas y la física. No solo nos permiten entender cómo cambian las funciones, sino que también nos ayudan a resolver problemas en situaciones reales. Imagina que estás en un coche, acelerando. ¿Cómo sabes cuán rápido estás yendo en un momento dado? Ahí es donde entran las derivadas. En este artículo, vamos a explorar cómo puedes mejorar tu comprensión de las derivadas a través de ejercicios prácticos y aplicaciones del mundo real. Así que, ¡prepárate para sumergirte en un viaje matemático!
¿Qué son las derivadas y por qué son importantes?
Antes de sumergirnos en los ejercicios, es esencial entender qué son las derivadas. En términos simples, la derivada de una función en un punto determinado nos dice la pendiente de la tangente a la curva en ese punto. Es como si estuvieras tratando de averiguar qué tan empinada es una montaña en un punto específico. ¿Es una pendiente suave o abrupta? Esa información es crucial en muchos campos, desde la ingeniería hasta la economía.
Aplicaciones prácticas de las derivadas
Las derivadas tienen aplicaciones en diversos campos. Por ejemplo, en economía, se utilizan para calcular el costo marginal, que es la derivada del costo total respecto a la cantidad producida. En física, se usan para entender el movimiento de los objetos, como la velocidad y la aceleración. ¿Ves cómo las derivadas están presentes en tu vida cotidiana, aunque no lo notes? Cada vez que tomas decisiones basadas en cambios o tendencias, estás utilizando principios derivados de las derivadas.
Ejercicios básicos de derivadas
Ahora que tenemos una base sólida, vamos a ver algunos ejercicios básicos que te ayudarán a comprender mejor el concepto de derivadas. No te preocupes si no eres un experto; la práctica es clave.
Ejercicio 1: Derivada de una función polinómica
Supongamos que tienes la función ( f(x) = x^2 + 3x + 5 ). ¿Cuál es la derivada de esta función? Para encontrar la derivada, aplicamos la regla de potencias. La derivada de ( x^n ) es ( nx^{n-1} ). Así que, para nuestra función:
1. La derivada de ( x^2 ) es ( 2x ).
2. La derivada de ( 3x ) es ( 3 ).
3. La derivada de una constante (5) es 0.
Por lo tanto, la derivada de ( f(x) ) es ( f'(x) = 2x + 3 ). ¡Fácil, verdad?
Ejercicio 2: Derivada de una función trigonométrica
Ahora, probemos algo un poco más complicado. Considera la función ( g(x) = sin(x) + cos(x) ). Las derivadas de las funciones trigonométricas son bastante conocidas:
1. La derivada de ( sin(x) ) es ( cos(x) ).
2. La derivada de ( cos(x) ) es ( -sin(x) ).
Así que, al derivar ( g(x) ), obtenemos:
g'(x) = cos(x) – sin(x).
¡Así de sencillo! Ahora, si quieres, intenta graficar ambas funciones y sus derivadas. Observa cómo la pendiente de la curva cambia en diferentes puntos.
Ejercicios intermedios de derivadas
Una vez que te sientas cómodo con los ejercicios básicos, es hora de pasar a algunos más desafiantes. Aquí es donde las derivadas se vuelven realmente interesantes.
Ejercicio 3: Regla del producto
Imagina que tienes dos funciones, ( u(x) = x^2 ) y ( v(x) = sin(x) ). Si quieres encontrar la derivada de su producto, necesitas usar la regla del producto, que dice que:
(uv)’ = u’v + uv’
Así que primero, encontramos las derivadas:
1. ( u’ = 2x )
2. ( v’ = cos(x) )
Ahora, aplicamos la regla del producto:
(uv)’ = (2x)(sin(x)) + (x^2)(cos(x)).
¡Y ahí lo tienes! La derivada del producto de dos funciones. Este es un buen ejemplo de cómo las derivadas se combinan para darnos información útil.
Ejercicio 4: Regla del cociente
Ahora, probemos con la regla del cociente. Supongamos que tienes la función ( h(x) = frac{x^2}{sin(x)} ). La regla del cociente nos dice que:
(f/g)’ = (f’g – fg’)/g²
Identificamos ( f = x^2 ) y ( g = sin(x) ), y encontramos las derivadas:
1. ( f’ = 2x )
2. ( g’ = cos(x) )
Ahora aplicamos la regla del cociente:
(h)’ = frac{(2x)(sin(x)) – (x^2)(cos(x))}{sin^2(x)}.
Con esto, tienes una comprensión más profunda de cómo se utilizan las derivadas en situaciones más complejas.
Ejercicios avanzados de derivadas
¿Listo para el siguiente nivel? Los ejercicios avanzados requieren un poco más de pensamiento crítico y creatividad. Pero no te preocupes, ¡estás más que preparado!
Ejercicio 5: Derivadas de funciones compuestas (Regla de la cadena)
Ahora, consideremos una función compuesta como ( j(x) = sin(x^2) ). Para encontrar la derivada, utilizamos la regla de la cadena, que dice que si ( y = f(g(x)) ), entonces:
y’ = f'(g(x)) * g'(x)
En nuestro caso, ( f(u) = sin(u) ) y ( g(x) = x^2 ). Primero, encontramos las derivadas:
1. ( f'(u) = cos(u) )
2. ( g'(x) = 2x )
Ahora aplicamos la regla de la cadena:
j'(x) = cos(x^2) * 2x.
¡Excelente trabajo! Ahora puedes ver cómo las derivadas se combinan en funciones compuestas.
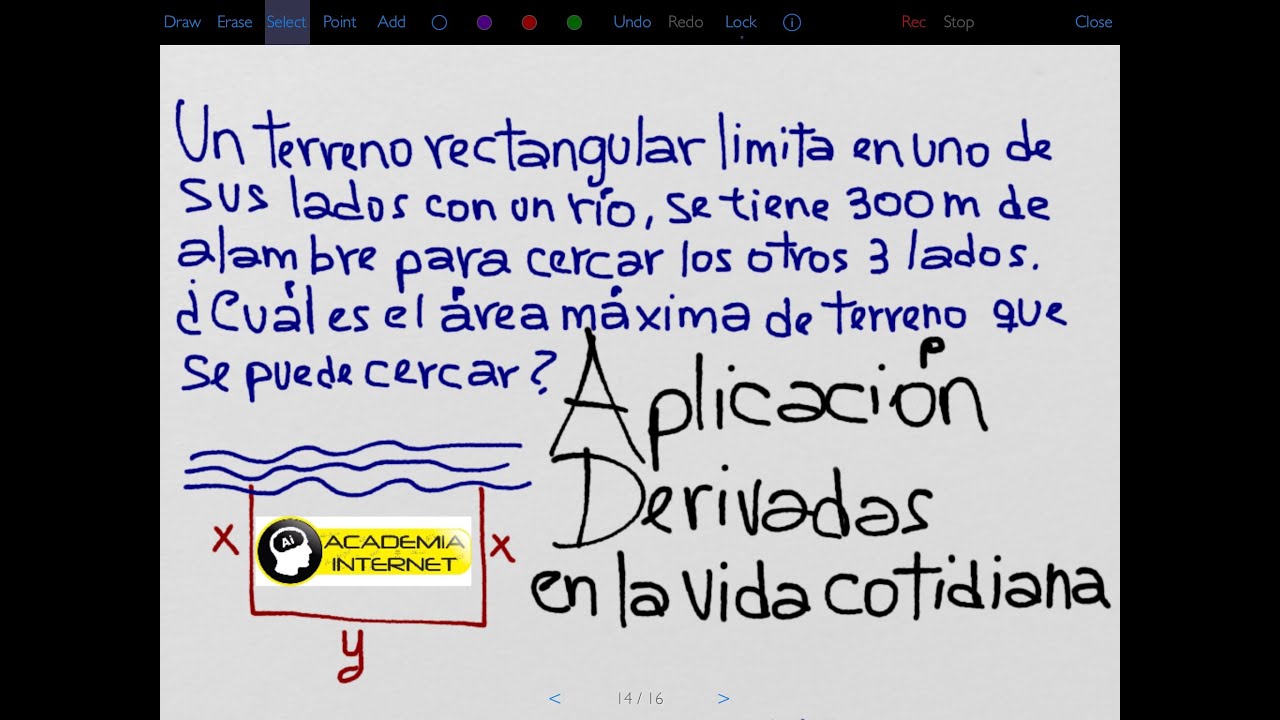
Ejercicio 6: Aplicaciones en problemas del mundo real
Finalmente, hablemos sobre cómo puedes aplicar lo que has aprendido. Imagina que estás diseñando un jardín y necesitas maximizar el área. Si tienes una función que describe el área en función de las dimensiones, puedes utilizar la derivada para encontrar los puntos críticos y determinar el tamaño óptimo del jardín. Esto no solo es matemático, sino que también es práctico y relevante.
Consejos para practicar derivadas
Practicar derivadas no tiene que ser aburrido. Aquí hay algunos consejos para hacer que el proceso sea más interesante:
- Usa software de matemáticas: Herramientas como Desmos o GeoGebra pueden ayudarte a visualizar funciones y sus derivadas.
- Trabaja en grupos: Explicar conceptos a otros puede solidificar tu comprensión.
- Aplica las derivadas a situaciones cotidianas: Intenta encontrar ejemplos en tu vida diaria donde puedas aplicar las derivadas, como en el análisis de datos de tus hábitos de compra o en la optimización de tiempo en tu rutina diaria.
¿Las derivadas son difíciles de entender?
Al principio pueden parecer complicadas, pero con práctica y ejemplos claros, se vuelven más comprensibles. ¡La clave es la práctica constante!
¿Cómo puedo mejorar en derivadas rápidamente?
Dedica tiempo a practicar diferentes tipos de ejercicios, desde los básicos hasta los avanzados. Además, no dudes en pedir ayuda o buscar recursos adicionales en línea.
¿Las derivadas tienen aplicaciones en la vida real?
¡Absolutamente! Desde la economía hasta la física y la biología, las derivadas son utilizadas para modelar y resolver problemas en una variedad de campos.
¿Cuál es la mejor manera de estudiar para un examen de derivadas?
Revisa tus notas, practica ejercicios, y considera formar un grupo de estudio. Asegúrate de entender los conceptos detrás de cada regla y cómo aplicarlos.
¿Las derivadas son útiles en la programación?
Sí, especialmente en el campo del aprendizaje automático y la optimización. Comprender las derivadas puede ayudarte a entender cómo funcionan ciertos algoritmos y modelos.
Recuerda, el viaje hacia la comprensión de las derivadas puede ser desafiante, pero con la práctica y la curiosidad, ¡puedes dominarlo!