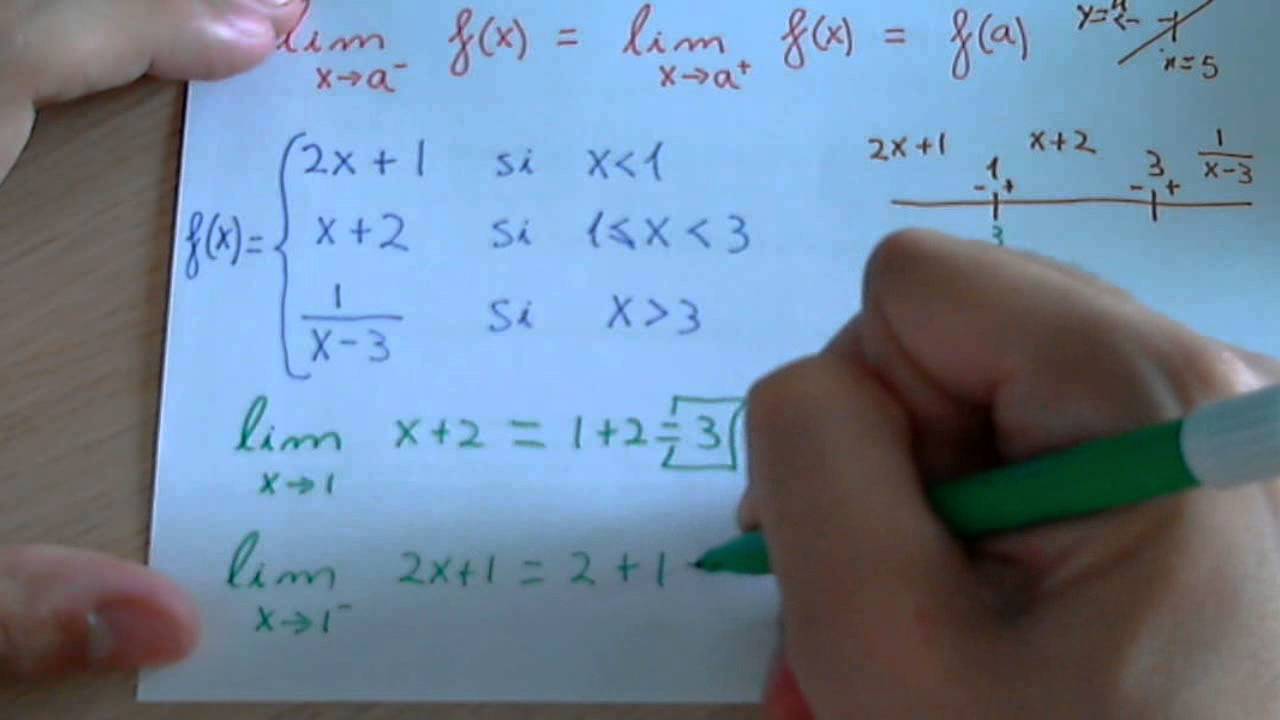¿Alguna vez te has encontrado con una función que parece no seguir el mismo camino que las demás? Las funciones discontinuas son como esos amigos que deciden cambiar de tema en medio de una conversación. A veces, se comportan de manera predecible, pero otras veces, ¡sorpresa! Te dejan en la incertidumbre. En este artículo, vamos a explorar qué son estas funciones, los diferentes tipos que existen, cómo se representan gráficamente y algunas aplicaciones prácticas. Así que, si estás listo para adentrarte en el fascinante mundo de las discontinuidades, ¡vamos a ello!
¿Qué son las Funciones Discontinuas?
Las funciones discontinuas son aquellas que no son continuas en algún punto o en todo su dominio. Esto significa que, al graficarlas, puedes notar que hay saltos, agujeros o incluso comportamientos extraños en su recorrido. Imagina que estás caminando por un sendero y, de repente, hay un agujero. Tienes que saltar para continuar, ¿verdad? Eso es lo que sucede con estas funciones. La discontinuidad puede ser clasificada en varios tipos, y cada uno tiene su propio carácter. ¿Te parece complicado? No te preocupes, desglosaremos todo esto.
Tipos de Discontinuidades
Discontinuidad Evitable
La discontinuidad evitable es como una broma que no tuvo gracia. Es un punto donde la función no está definida, pero podrías haberla definido de una manera que tuviera sentido. Por ejemplo, si tenemos la función f(x) = (x^2 – 1)/(x – 1), esta función no está definida en x = 1 porque resulta en una división por cero. Sin embargo, si simplificamos la expresión, vemos que f(x) puede ser 1 en todos los demás puntos. Así que, aunque la función «se detiene» en x = 1, podríamos haber evitado esa discontinuidad.
Discontinuidad Infinita
Ahora, pasemos a la discontinuidad infinita. Imagina que estás en un juego de video y de repente, te enfrentas a un jefe que tiene un poder desmesurado. Eso es lo que ocurre en esta situación. En ciertos puntos, la función tiende al infinito, lo que significa que su valor crece sin límite. Un ejemplo clásico es la función f(x) = 1/(x – 2). Aquí, cuando x se acerca a 2, f(x) se dispara hacia el infinito. ¡Cuidado con ese jefe!
Discontinuidad Oscilante
La discontinuidad oscilante es como un péndulo que no puede decidir hacia dónde ir. En esta situación, la función oscila entre dos valores a medida que te acercas a un punto específico. Un ejemplo sería la función f(x) = sin(1/x) cuando x se aproxima a 0. La función no se estabiliza en un valor específico, sino que sigue oscilando, haciendo que no podamos definir un límite claro. Es como tratar de atrapar a un pez en el agua, siempre se escapa.
Gráficas de Funciones Discontinuas
Ahora que ya tenemos una idea de qué son las funciones discontinuas y sus tipos, es hora de ver cómo se ven gráficamente. Las gráficas son la representación visual que nos ayuda a entender mejor el comportamiento de estas funciones.
Gráfica de una Discontinuidad Evitable
Cuando graficamos una discontinuidad evitable, como la función f(x) = (x^2 – 1)/(x – 1), notarás que hay un agujero en la gráfica en x = 1. A pesar de que el valor de la función podría ser 1 en otros puntos, la gráfica «se detiene» en ese punto. Es como si estuvieras viendo una película que se detiene justo antes del clímax.
Gráfica de una Discontinuidad Infinita
En el caso de la discontinuidad infinita, la gráfica se disparará hacia el infinito en el punto de discontinuidad. En el ejemplo de f(x) = 1/(x – 2), verás que a medida que te acercas a x = 2, la gráfica se eleva sin límites. Es como ver una montaña rusa que se eleva cada vez más y más, dejando a los pasajeros con la adrenalina al máximo.
Gráfica de una Discontinuidad Oscilante
Para la discontinuidad oscilante, la gráfica se verá como un vaivén frenético. En el caso de f(x) = sin(1/x), al acercarte a x = 0, notarás que la gráfica oscila entre -1 y 1, sin detenerse. Es como un baile constante que no parece tener un final claro. Esta oscilación puede ser desconcertante, pero también es fascinante ver cómo la función se comporta de manera tan impredecible.
Aplicaciones de las Funciones Discontinuas
Las funciones discontinuas pueden parecer solo un tema teórico, pero en realidad, tienen aplicaciones prácticas en diversos campos. Desde la física hasta la economía, entender estas discontinuidades puede ser crucial.
Física y Ingeniería
En física, las funciones discontinuas pueden modelar fenómenos como el comportamiento de materiales bajo tensión. Por ejemplo, al analizar cómo se comporta un material cuando se le aplica una fuerza, podrías encontrar que hay puntos donde el material se rompe o se deforma de manera abrupta. Aquí, las discontinuidades son vitales para entender la resistencia de los materiales.
Economía
En el ámbito económico, las funciones discontinuas pueden aparecer en situaciones de cambio abrupto, como en el caso de los precios de acciones. Si una empresa anuncia una fusión o una quiebra, el precio de sus acciones puede experimentar un salto repentino. Estos cambios bruscos son ejemplos de discontinuidades que pueden ser analizadas para tomar decisiones informadas en inversiones.
Biología
En biología, las funciones discontinuas pueden ayudar a modelar poblaciones de especies que experimentan cambios drásticos debido a factores externos. Por ejemplo, una especie podría multiplicarse rápidamente hasta que un depredador aparezca, causando una caída repentina en la población. Estas discontinuidades son esenciales para entender dinámicas ecológicas complejas.
Las funciones discontinuas son un concepto fascinante que nos muestra cómo el mundo puede comportarse de maneras inesperadas. Desde las discontinuidades evitables hasta las oscilantes, cada tipo ofrece una visión única de cómo las funciones pueden cambiar abruptamente. Al entender estas discontinuidades, no solo estamos aprendiendo matemáticas, sino también cómo aplicar este conocimiento en el mundo real. Así que la próxima vez que veas una función con un salto o un agujero, recuerda que hay mucho más de lo que parece a simple vista.
¿Por qué son importantes las funciones discontinuas en matemáticas?
Las funciones discontinuas son importantes porque nos ayudan a entender comportamientos no lineales y situaciones donde las reglas normales no se aplican. Son esenciales en el análisis de límites y en la comprensión de fenómenos en el mundo real.
¿Cómo puedo identificar una discontinuidad en una función?
Para identificar una discontinuidad, observa el comportamiento de la función en diferentes puntos. Si encuentras un punto donde la función no está definida o cambia abruptamente, probablemente estés ante una discontinuidad.
¿Las funciones discontinuas tienen aplicaciones prácticas?
¡Absolutamente! Se utilizan en campos como la física, la economía y la biología para modelar fenómenos que presentan cambios abruptos o comportamientos inusuales.
¿Se pueden resolver discontinuidades en funciones?
En algunos casos, sí. Las discontinuidades evitables se pueden «resolver» al redefinir la función en ese punto. Sin embargo, las discontinuidades infinitas y oscilantes pueden requerir un análisis más profundo.
¿Qué pasa si una función tiene múltiples discontinuidades?
Una función puede tener múltiples discontinuidades y cada una puede ser de diferentes tipos. Es importante analizarlas individualmente para entender el comportamiento general de la función.