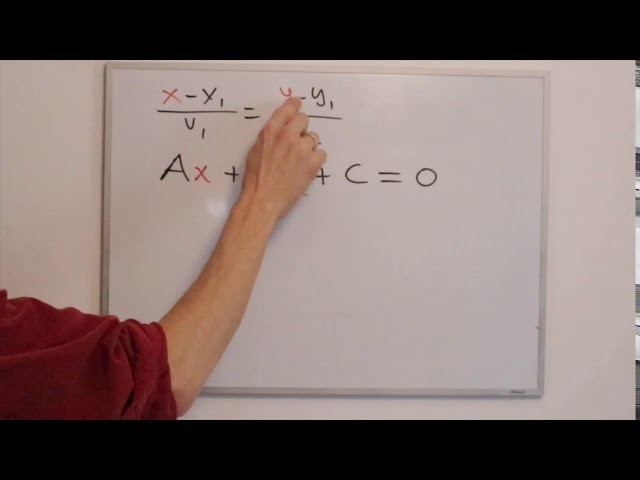Entendiendo la Ecuación Implícita: Un Viaje a Través de las Matemáticas
¿Alguna vez te has preguntado cómo se puede describir una recta en el plano cartesiano? Bueno, la respuesta está en las ecuaciones, y hoy vamos a sumergirnos en el fascinante mundo de la ecuación implícita de una recta. Antes de que te asustes con términos técnicos, permíteme asegurarte que no es tan complicado como parece. La ecuación de una recta puede parecer un simple conjunto de números y letras, pero detrás de ella hay una lógica y una belleza que vale la pena explorar. Así que, siéntate, relájate y acompáñame en este viaje matemático.
¿Qué es una Ecuación Implícita?
Primero, hablemos de qué es exactamente una ecuación implícita. En términos simples, una ecuación implícita de una recta es aquella que no está despejada para una de las variables. Por ejemplo, en lugar de tener algo como y = mx + b, que es la forma explícita de la ecuación de una recta, la forma implícita podría verse así: Ax + By + C = 0. Aquí, A, B, y C son constantes que definen la recta. Esta forma puede parecer más enrevesada, pero en realidad, es igual de válida y útil.
¿Por qué Usar la Ecuación Implícita?
Ahora, te estarás preguntando: «¿Por qué debería preocuparme por la ecuación implícita si puedo usar la forma explícita?» Bueno, la respuesta es simple. La ecuación implícita es especialmente útil en situaciones donde es complicado despejar y o cuando se trabaja con múltiples ecuaciones. Imagina que estás en un juego de ajedrez, y tienes que prever varios movimientos a la vez. La ecuación implícita te permite manejar situaciones más complejas sin tener que resolver cada una por separado. Además, es muy utilizada en geometría analítica y en el estudio de cónicas.
La Forma General de la Ecuación de una Recta
Ahora que hemos establecido qué es una ecuación implícita, hablemos de su forma general. La ecuación Ax + By + C = 0 se considera la forma general de la ecuación de una recta. Aquí, A y B no pueden ser ambos cero. Este tipo de ecuación puede representar tanto rectas verticales como horizontales, lo que la convierte en una herramienta poderosa para describir cualquier línea en el plano.
Componentes de la Ecuación
Desglosando la ecuación, A es el coeficiente que afecta la inclinación de la recta. Si A es positivo, la recta sube hacia la derecha; si es negativo, baja. Por otro lado, B influye en la inclinación en el eje y. Y, por último, C es simplemente un desplazamiento vertical de la recta. Al cambiar estos valores, puedes ver cómo la recta se desplaza y se gira en el plano. Es como si tuvieras un control remoto para manipular la línea a tu antojo.
Cómo Graficar una Ecuación Implícita
¿Listo para poner manos a la obra? Graficar una ecuación implícita puede parecer complicado, pero te prometo que es más sencillo de lo que parece. Lo primero que necesitas hacer es encontrar algunos puntos que satisfagan la ecuación. Para hacer esto, puedes elegir valores para x y resolver para y, o viceversa. Una vez que tengas varios puntos, simplemente traza esos puntos en un plano cartesiano y une los puntos con una línea. ¡Y voilà! Tienes tu recta.
Ejemplo Práctico
Imagina que tienes la ecuación 2x + 3y – 6 = 0. Puedes elegir algunos valores para x. Digamos que eliges x = 0. Sustituyendo en la ecuación, obtienes 3y – 6 = 0, lo que significa que y = 2. Ahora, elige x = 3, y obtendrás 3y – 12 = 0, por lo que y = 4. Con estos dos puntos, (0, 2) y (3, 4), puedes graficar tu recta. ¡Sencillo, verdad?
Propiedades de la Ecuación Implícita
Las ecuaciones implícitas tienen varias propiedades interesantes que pueden ser útiles al trabajar con ellas. Una de las más importantes es que la forma implícita puede ser transformada a la forma explícita. Esto es especialmente útil si necesitas la ecuación en un formato que sea más fácil de trabajar. Simplemente despeja y y tendrás la forma y = mx + b.
Intersección de Rectas
Otra propiedad fascinante es la intersección de dos rectas. Cuando tienes dos ecuaciones implícitas, puedes encontrar su punto de intersección resolviendo el sistema de ecuaciones. Esto es como resolver un rompecabezas: tienes que encontrar el lugar donde ambas rectas se cruzan. Una vez que encuentres ese punto, tendrás una mejor comprensión de cómo se relacionan esas dos rectas entre sí.
Aplicaciones de la Ecuación Implícita
Las aplicaciones de las ecuaciones implícitas son vastas y variadas. Desde la física hasta la economía, estas ecuaciones pueden modelar situaciones del mundo real. Por ejemplo, en física, se utilizan para describir trayectorias de objetos en movimiento. En economía, pueden representar relaciones entre diferentes variables económicas. Así que, la próxima vez que veas una ecuación implícita, recuerda que detrás de ella hay un mundo de aplicaciones prácticas.
Desafíos Comunes
A pesar de su utilidad, trabajar con ecuaciones implícitas puede presentar algunos desafíos. Uno de los más comunes es la dificultad para despejar variables. A veces, la ecuación puede volverse bastante complicada y puede que necesites recurrir a técnicas de álgebra más avanzadas. Sin embargo, con un poco de práctica, estos desafíos se vuelven más manejables. Es como aprender a andar en bicicleta: al principio puede parecer difícil, pero con el tiempo, se vuelve natural.
¿Qué es la diferencia entre la forma implícita y la forma explícita de una ecuación de recta?
La forma explícita es aquella donde una variable está despejada, como y = mx + b, mientras que la forma implícita es un conjunto de variables que no están despejadas, como Ax + By + C = 0.
¿Puedo usar la ecuación implícita para representar una recta vertical?
¡Sí! Una recta vertical se puede representar con una ecuación implícita como x = a, donde a es un valor constante. En este caso, la forma general sería 1x + 0y – a = 0.
¿Cómo puedo transformar una ecuación implícita en explícita?
Para transformar una ecuación implícita en explícita, simplemente despeja la variable y (o x, dependiendo de la ecuación) de la ecuación. Esto te dará la forma y = mx + b.
¿Las ecuaciones implícitas son utilizadas en cálculo?
Sí, las ecuaciones implícitas son fundamentales en cálculo, especialmente en la derivación y el análisis de funciones. La derivación implícita es una técnica utilizada para encontrar la derivada de una función que no está explícitamente resuelta.
En conclusión, la ecuación implícita de una recta es una herramienta poderosa y versátil que puede ser utilizada en diversas disciplinas. No subestimes su valor, ya que detrás de una simple ecuación puede haber un mundo de aplicaciones y conexiones. Así que, la próxima vez que te enfrentes a una ecuación implícita, recuerda que tienes el poder de desentrañar sus secretos y descubrir lo que hay detrás de ella. ¡Feliz aprendizaje!