Cuando hablamos de funciones en matemáticas, es como si estuviéramos hablando de una máquina mágica que transforma un conjunto de números en otro. Pero, ¿alguna vez te has preguntado qué significa realmente el «dominio» y el «recorrido» de una función? Si alguna vez te has sentido perdido en este tema, no te preocupes. En esta guía completa, desglosaremos estos conceptos de manera sencilla y clara, como si estuviéramos conversando entre amigos. Prepárate para explorar el fascinante mundo de las funciones y cómo se aplican en diferentes contextos.
¿Qué es el Dominio de una Función?
El dominio de una función es el conjunto de todos los valores de entrada que podemos usar sin causar problemas. Piensa en él como la lista de invitados a una fiesta: solo aquellos que están en la lista pueden entrar. En el mundo de las funciones, algunos números simplemente no están invitados. Por ejemplo, si tienes una función que incluye una raíz cuadrada, como √x, no puedes usar números negativos, porque la raíz cuadrada de un número negativo no está definida en el conjunto de los números reales. Así que, en este caso, el dominio sería todos los números reales mayores o iguales a cero.
Ejemplos Prácticos del Dominio
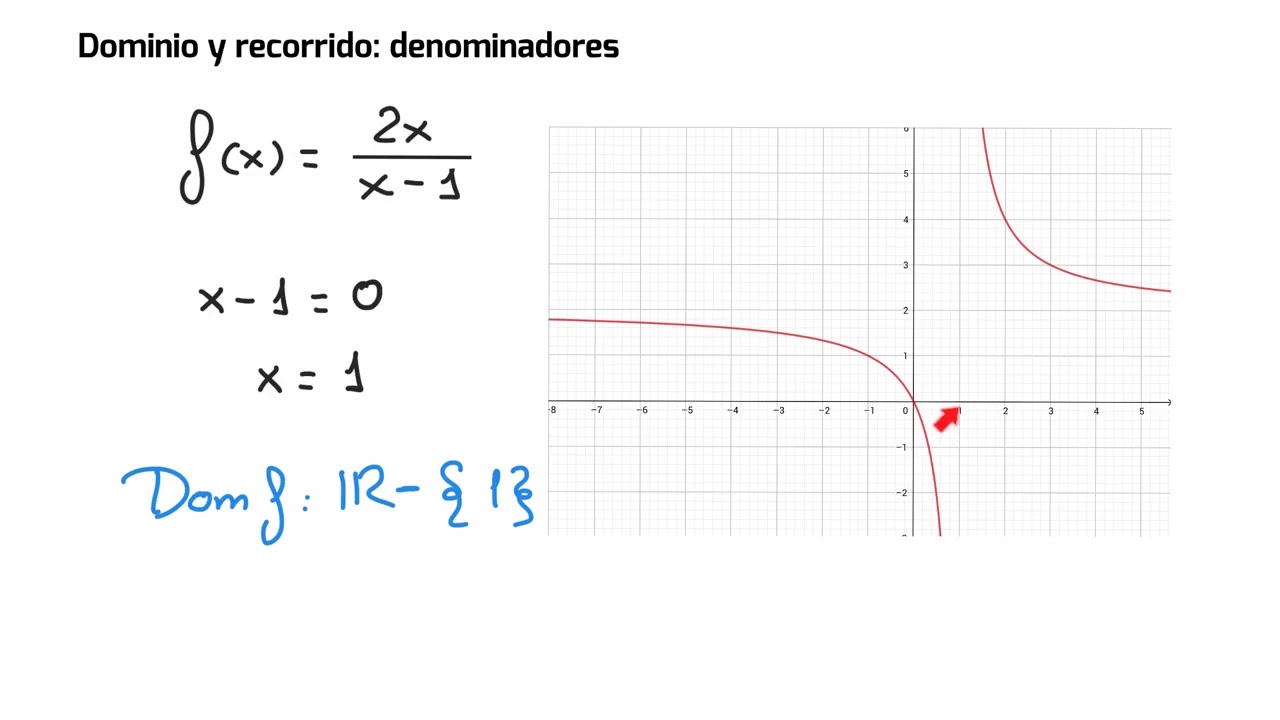
Imagina que tienes la función f(x) = 1/x. Aquí, el dominio se ve afectado porque no podemos dividir entre cero. Así que, el dominio de esta función sería todos los números reales excepto cero. ¡Y ahí lo tienes! Un simple vistazo a la función y ya sabes qué números son bienvenidos a la fiesta. A veces, el dominio puede ser un poco más complicado, especialmente cuando se trata de funciones polinómicas, trigonométricas o logarítmicas. Pero no te preocupes, más adelante profundizaremos en esos ejemplos.
¿Qué es el Recorrido de una Función?
Si el dominio es la lista de invitados, el recorrido es como la experiencia de la fiesta. Es el conjunto de todos los valores de salida que la función puede producir. En otras palabras, una vez que tus amigos (valores de entrada) han llegado a la fiesta, ¿qué tipo de diversión (valores de salida) pueden esperar? Por ejemplo, si consideras la función f(x) = x², el recorrido es todos los números reales no negativos, ya que cualquier número que elijas elevar al cuadrado nunca será negativo.
Ejemplos del Recorrido en Acción
Supongamos que tenemos la función f(x) = -x². Aquí, el recorrido será todos los números reales menores o iguales a cero. Esto es interesante porque, aunque el dominio puede ser todos los números reales, el recorrido está restringido a valores negativos o cero. Es como si tu fiesta tuviera un tema específico y solo se permitieran ciertos tipos de diversión.
Cómo Encontrar el Dominio y el Recorrido
Ahora que entendemos los conceptos básicos, hablemos de cómo encontrar el dominio y el recorrido de una función. ¡No te asustes! Aunque puede parecer complicado al principio, con un poco de práctica, se vuelve mucho más fácil.
Pasos para Encontrar el Dominio
- Identifica restricciones: Busca cualquier operación que pueda causar problemas, como divisiones por cero o raíces cuadradas de números negativos.
- Escribe el dominio: Una vez que identifiques las restricciones, escribe el dominio usando notación de intervalos o en forma de conjunto.
Por ejemplo, para la función f(x) = √(x – 3), primero identificamos que la expresión dentro de la raíz debe ser mayor o igual a cero. Esto nos da la restricción x – 3 ≥ 0, lo que significa que x debe ser mayor o igual a 3. Así que el dominio es [3, ∞).
Pasos para Encontrar el Recorrido
- Determina el comportamiento de la función: Analiza cómo se comporta la función a medida que los valores de entrada cambian. ¿Alcanza un máximo o un mínimo?
- Escribe el recorrido: Basándote en el comportamiento que observaste, escribe el recorrido en notación de intervalos o en forma de conjunto.
Por ejemplo, con la función f(x) = x², a medida que x toma valores de entrada desde -∞ hasta +∞, el valor de f(x) siempre será mayor o igual a cero. Por lo tanto, el recorrido es [0, ∞).
Aplicaciones del Dominio y Recorrido en el Mundo Real
¿Te has preguntado alguna vez cómo estos conceptos se aplican en la vida real? La verdad es que están en todas partes. Desde la economía hasta la biología, el dominio y el recorrido de las funciones nos ayudan a modelar situaciones y tomar decisiones informadas.
Ejemplo en Economía
Imagina que eres un economista tratando de predecir el costo de producción de un producto en función de la cantidad producida. La función que modela esta relación puede tener un dominio específico, ya que no puedes producir una cantidad negativa de productos. Al analizar el recorrido, puedes determinar el costo mínimo y máximo que podrías esperar, lo que es vital para establecer precios y maximizar ganancias.
Ejemplo en Biología
En biología, podrías encontrar funciones que describen el crecimiento de una población. Aquí, el dominio representaría el tiempo y el recorrido podría representar la población en diferentes momentos. Al entender estos conceptos, los biólogos pueden predecir cómo cambiará la población bajo ciertas condiciones, lo que es crucial para la conservación de especies y el manejo de ecosistemas.
Errores Comunes y Cómo Evitarlos
Es fácil cometer errores al trabajar con el dominio y el recorrido, especialmente si no se prestan atención a los detalles. Aquí hay algunos errores comunes y cómo puedes evitarlos:
Olvidar las Restricciones
Un error común es olvidar considerar las restricciones en el dominio. Asegúrate de revisar cada parte de la función y preguntar: «¿Este número es válido?»
Confundir Dominio y Recorrido
Otro error frecuente es confundir el dominio con el recorrido. Recuerda: el dominio son los valores de entrada y el recorrido son los valores de salida. Mantén esta distinción clara en tu mente.
¿Puedo tener un dominio infinito?
¡Sí! Muchas funciones, como los polinomios, tienen un dominio que abarca todos los números reales, lo que significa que puedes usar cualquier número como entrada.
¿El recorrido siempre es un intervalo cerrado?
No necesariamente. El recorrido puede ser un intervalo abierto o cerrado, dependiendo de la función. Asegúrate de analizar bien la función para determinar la naturaleza del recorrido.
¿Qué sucede si no puedo encontrar el dominio o el recorrido?
Si te encuentras en un punto muerto, no dudes en pedir ayuda o buscar ejemplos similares. A veces, ver cómo otros han resuelto problemas puede aclarar tus dudas.
¿Por qué son importantes el dominio y el recorrido en matemáticas?
Son fundamentales para comprender cómo se comportan las funciones y cómo se relacionan los valores de entrada con los de salida. Sin esta comprensión, sería difícil aplicar funciones en problemas del mundo real.
En resumen, el dominio y el recorrido son conceptos clave que te ayudarán a navegar por el mundo de las funciones matemáticas. Ya sea que estés estudiando para un examen o simplemente tengas curiosidad, entender estos temas te abrirá un nuevo horizonte en tu aprendizaje. ¡Así que adelante, explora y diviértete con las funciones!