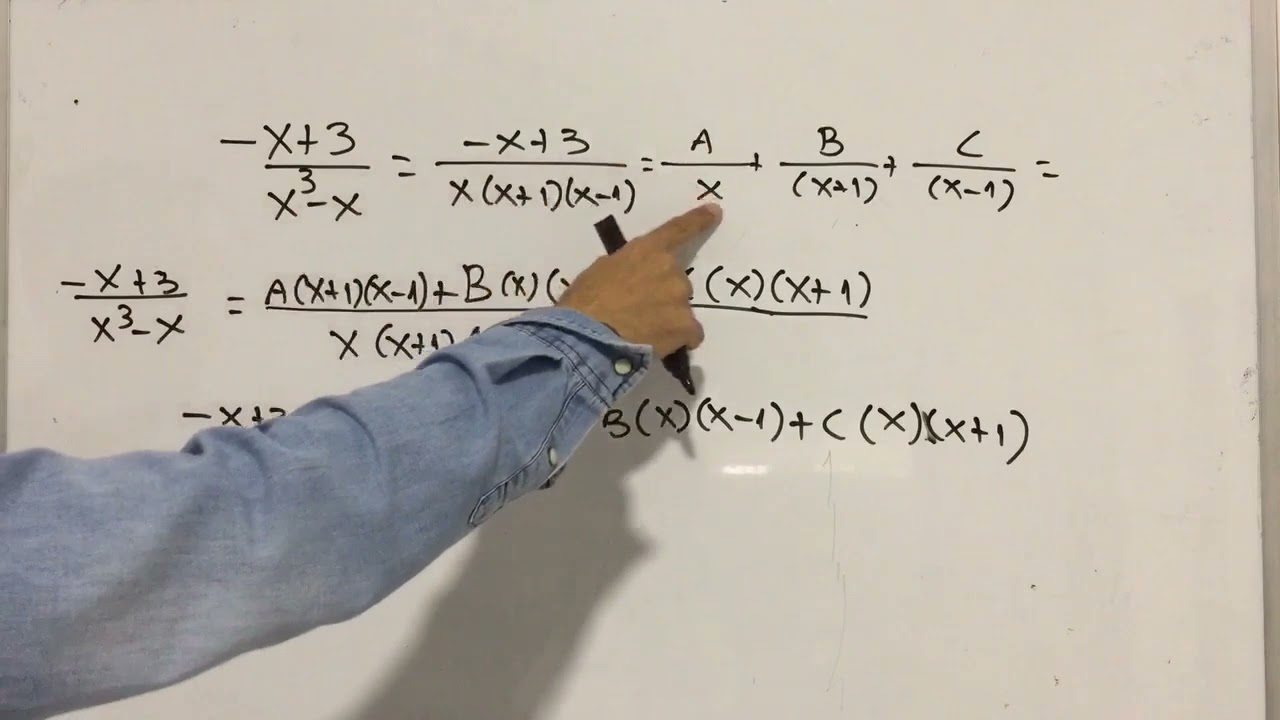¿Alguna vez te has encontrado con una fracción algebraica y te has preguntado cómo descomponerla en fracciones más simples? ¡No te preocupes! Estás en el lugar correcto. En este artículo, te guiaré a través de un proceso paso a paso que te ayudará a descomponer fracciones algebraicas en fracciones elementales. Imagina que estás armando un rompecabezas; cada pieza tiene su lugar y, cuando las unes, obtienes una imagen clara. Así es como funcionan las fracciones elementales: al descomponer una fracción compleja, revelamos partes más simples que son mucho más fáciles de manejar. ¡Vamos a sumergirnos en el fascinante mundo de las fracciones algebraicas!
¿Qué son las Fracciones Algebraicas?
Antes de adentrarnos en el proceso de descomposición, es fundamental entender qué son las fracciones algebraicas. Estas son expresiones que tienen polinomios en el numerador y el denominador. Por ejemplo, una fracción como (2x^2 + 3)/(x^2 – 1) es una fracción algebraica. A menudo, estas fracciones son el resultado de operaciones más complejas y pueden parecer intimidantes al principio. Sin embargo, con un poco de práctica y algunos pasos sencillos, podrás descomponerlas sin problemas.
Pasos para Descomponer una Fracción Algebraica
Paso 1: Factoriza el Denominador
El primer paso en la descomposición de una fracción algebraica es factorizar el denominador. Esto significa que debemos encontrar los factores que, al multiplicarse, nos devuelven el polinomio original. Por ejemplo, si nuestro denominador es x^2 – 1, podemos factorizarlo como (x – 1)(x + 1). ¿Por qué es importante? Porque al conocer los factores, podemos identificar las fracciones elementales que formarán parte de nuestra descomposición.
Paso 2: Establecer la Forma de la Fracción Elemental
Una vez que tenemos el denominador factorizado, el siguiente paso es establecer la forma que tendrán las fracciones elementales. Para cada factor del denominador, creamos una fracción. Siguiendo nuestro ejemplo anterior, con (x – 1)(x + 1), podemos establecer que la descomposición tendrá la forma:
- A/(x – 1) + B/(x + 1)
Donde A y B son constantes que necesitamos determinar. Piensa en esto como si estuvieras preparando los ingredientes para una receta; cada ingrediente (o constante) tiene un papel crucial en el resultado final.
Paso 3: Multiplicar por el Denominador Común
Ahora que tenemos la forma de nuestra fracción elemental, el siguiente paso es multiplicar ambos lados de la ecuación por el denominador común, que en este caso es (x – 1)(x + 1). Esto nos ayudará a eliminar el denominador y simplificar la ecuación. Al hacerlo, obtendremos:
- 2x^2 + 3 = A(x + 1) + B(x – 1)
Al igual que cuando limpias una pizarra para ver mejor lo que has escrito, multiplicar por el denominador común nos permite ver más claramente la relación entre las variables.
Paso 4: Resolver para las Constantes
Ahora es el momento de resolver para las constantes A y B. Para hacer esto, podemos elegir valores específicos de x que simplifiquen la ecuación. Por ejemplo, si elegimos x = 1, podemos sustituir este valor en la ecuación y resolver:
- 2(1)^2 + 3 = A(1 + 1) + B(1 – 1)
- 5 = 2A
De aquí, podemos deducir que A = 5/2. Ahora, repitiendo este proceso con otro valor, como x = -1, podemos encontrar B.
Paso 5: Sustitución y Comprobación
Una vez que tenemos ambos valores, A y B, podemos sustituirlos de nuevo en la forma de la fracción elemental. Así que, siguiendo nuestro ejemplo, la descomposición final será:
- 5/2(x – 1) + (-1/2)(x + 1)
Es crucial comprobar nuestra respuesta. ¿Cómo? Simplemente sumando las fracciones elementales que obtuvimos y asegurándonos de que el resultado coincida con la fracción algebraica original. Si todo se alinea, ¡felicidades! Has descompuesto exitosamente una fracción algebraica.
Ejemplo Práctico
Para solidificar lo que hemos aprendido, veamos un ejemplo práctico. Supongamos que queremos descomponer la fracción algebraica:
- (3x^2 + 5)/(x^2 – 4)
Siguiendo los pasos que hemos mencionado, comenzamos por factorizar el denominador:
- x^2 – 4 = (x – 2)(x + 2)
Luego, establecemos la forma de las fracciones elementales:
- A/(x – 2) + B/(x + 2)
Multiplicamos por el denominador común:
- 3x^2 + 5 = A(x + 2) + B(x – 2)
Resolviendo para A y B usando valores de x, encontramos que A = 2 y B = 1. Por lo tanto, la descomposición es:
- 2/(x – 2) + 1/(x + 2)
Comprobamos y, efectivamente, se alinea con la fracción original. ¡Lo hicimos!
Consejos para Descomponer Fracciones Algebraicas
Práctica Regular
La práctica es esencial. Cuanto más trabajes con fracciones algebraicas, más cómodo te sentirás. No dudes en crear tus propios ejemplos o buscar ejercicios en línea para afianzar tus conocimientos.
Utiliza Recursos Visuales
Si eres una persona visual, considera utilizar gráficos o diagramas. A veces, ver el proceso puede ayudarte a entenderlo mejor. Puedes incluso dibujar el proceso de descomposición como si fueras un artista creando una obra maestra.
No Te Rindas
Al principio, puede parecer complicado, pero recuerda que cada matemático ha estado donde tú estás ahora. La perseverancia es clave. ¡No te desanimes y sigue practicando!
¿Es necesario factorizar el denominador siempre?
Sí, la factorización del denominador es crucial para poder descomponer correctamente la fracción. Sin esto, no podrás establecer las fracciones elementales adecuadamente.
¿Qué hago si el denominador no se puede factorizar?
Si el denominador no se puede factorizar, puedes usar métodos como la división sintética o la regla de Ruffini para intentar simplificar la fracción. En algunos casos, es posible que debas utilizar fracciones impropias.
¿Puedo descomponer fracciones algebraicas con exponentes negativos?
¡Claro! Las fracciones algebraicas pueden incluir exponentes negativos. Simplemente sigue los mismos pasos y asegúrate de manejar los signos correctamente.
¿Es útil la descomposición de fracciones algebraicas en la vida real?
Definitivamente. La descomposición de fracciones algebraicas es fundamental en muchas áreas, como la ingeniería, la economía y las ciencias. Te ayuda a simplificar problemas complejos y a resolver ecuaciones de manera más eficiente.
¿Dónde puedo encontrar más ejercicios sobre este tema?
Existen numerosos recursos en línea, desde plataformas educativas hasta libros de texto que ofrecen ejercicios prácticos. ¡Explora y encuentra el que más te guste!