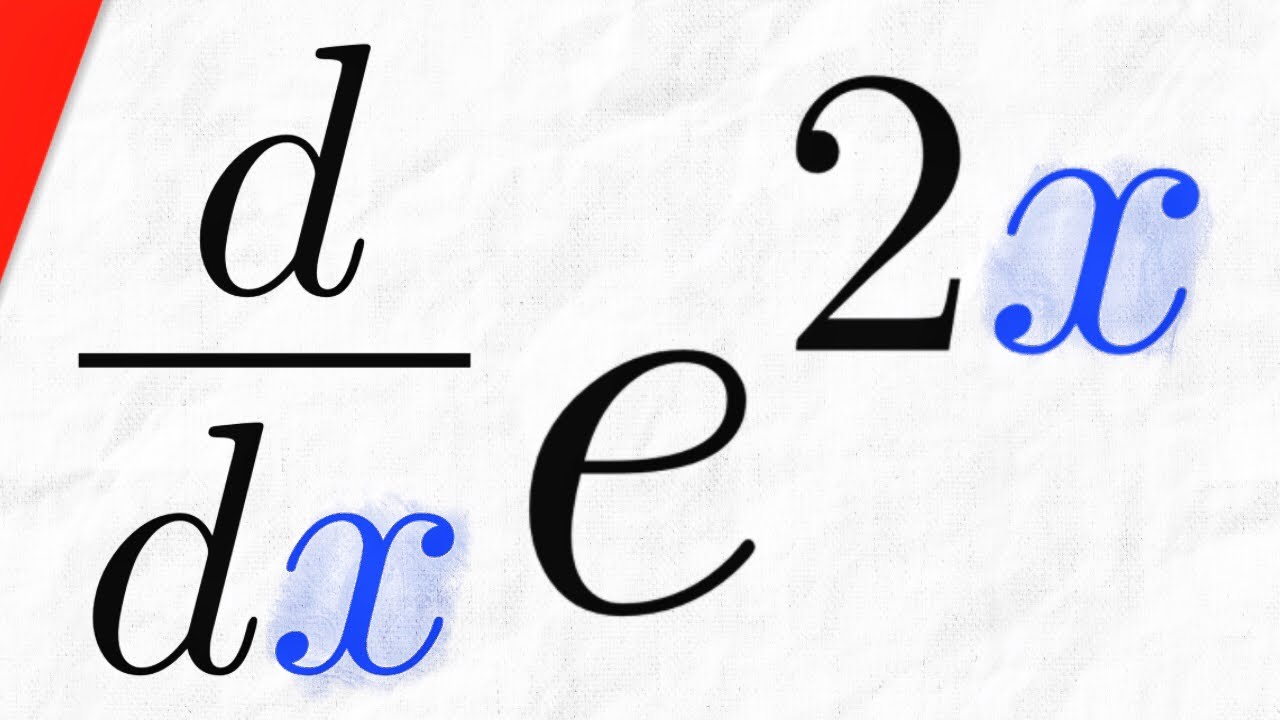¿Alguna vez te has preguntado cómo se calcula la derivada de una función? ¡No estás solo! La derivada es un concepto fundamental en cálculo que nos permite entender cómo cambian las funciones. En este artículo, vamos a explorar de manera sencilla y práctica cómo calcular la derivada de la función 2x. Pero antes de sumergirnos en los detalles, hablemos un poco sobre qué es una derivada y por qué es importante.
La derivada de una función en un punto específico nos dice la pendiente de la tangente a la curva en ese punto. Imagina que estás conduciendo por una carretera montañosa: la pendiente de la carretera en un momento dado te dirá si estás subiendo o bajando. De manera similar, la derivada nos proporciona información sobre cómo cambia el valor de la función en relación con su variable independiente. Ahora, vamos a desglosar el proceso de calcular la derivada de 2x paso a paso.
¿Qué es la Derivada?
Para comenzar, es crucial entender el concepto de derivada. En términos simples, la derivada de una función f(x) se define como el límite del cociente de la diferencia cuando el incremento en x tiende a cero. Esto puede sonar un poco técnico, pero no te preocupes, lo desglosaremos.
Si tienes una función, como f(x) = 2x, su derivada se puede interpretar como la tasa de cambio de la función respecto a x. En otras palabras, ¿cuánto cambia f(x) cuando cambias x un poquito? Este cambio es lo que queremos calcular. La notación comúnmente utilizada para la derivada es f'(x) o df/dx.
Pasos para Calcular la Derivada de 2x
Ahora que tenemos una idea básica de lo que es la derivada, vamos a adentrarnos en los pasos específicos para calcular la derivada de 2x. ¡Vamos a hacerlo juntos!
Paso 1: Identificar la Función
El primer paso es identificar la función de la que queremos encontrar la derivada. En este caso, nuestra función es f(x) = 2x. Aquí, 2 es un coeficiente y x es la variable independiente.
Paso 2: Aplicar la Regla de Potencias
La regla de potencias es una herramienta poderosa en cálculo. Según esta regla, si tienes una función de la forma f(x) = ax^n, donde a es una constante y n es un número real, la derivada se calcula como:
f'(x) = a * n * x^(n-1)
Para nuestra función 2x, podemos reescribirla como 2x^1. Aquí, a = 2 y n = 1. Ahora, aplicamos la regla de potencias:
f'(x) = 2 * 1 * x^(1-1) = 2 * 1 * x^0 = 2 * 1 * 1 = 2
Así que la derivada de 2x es simplemente 2. ¡Fácil, verdad?
Paso 3: Interpretar el Resultado
Una vez que hemos calculado la derivada, es importante entender lo que significa. La derivada f'(x) = 2 nos dice que la pendiente de la línea tangente a la función 2x es constante e igual a 2 en cualquier punto de la función. Esto significa que, sin importar el valor de x, la función está aumentando a un ritmo constante.
Imagina que estás en una pista de carreras: si la pendiente es 2, eso significa que por cada unidad que avanzas en el eje x, subes 2 unidades en el eje y. ¡Eso es un ascenso constante!
Ejemplos Prácticos
Para reforzar lo que hemos aprendido, veamos algunos ejemplos prácticos de cómo aplicar el cálculo de la derivada a otras funciones.
Ejemplo 1: Derivada de 3x^2
Supongamos que queremos encontrar la derivada de f(x) = 3x^2. Aquí, a = 3 y n = 2. Aplicamos la regla de potencias:
f'(x) = 3 * 2 * x^(2-1) = 6x^1 = 6x.
Esto nos dice que la pendiente de la función 3x^2 varía con x, pero siempre será positiva cuando x sea positivo.
Ejemplo 2: Derivada de x^3 – 4x
Ahora, calculemos la derivada de f(x) = x^3 – 4x. Aquí tenemos dos términos, así que aplicamos la regla de potencias a cada uno:
f'(x) = 3x^(3-1) – 4(1)x^(1-1) = 3x^2 – 4.
La derivada aquí nos dice que la pendiente de la función cambia según el valor de x, lo que hace que esta función sea un poco más interesante.
Aplicaciones de la Derivada
Las derivadas no son solo un concepto teórico; tienen aplicaciones prácticas en el mundo real. Veamos algunas de estas aplicaciones.
Optimización
Uno de los usos más comunes de las derivadas es en problemas de optimización. Por ejemplo, si tienes una función que representa el costo de producción de un producto, puedes usar la derivada para encontrar el punto en el que los costos son mínimos. Esto es crucial para cualquier negocio que quiera maximizar sus ganancias.
Movimiento y Velocidad
En física, la derivada se utiliza para calcular la velocidad. Si tienes la posición de un objeto en función del tiempo, la derivada de esa función te dará la velocidad instantánea del objeto. Imagina que estás monitoreando un coche en una carrera: al calcular la derivada de su posición, puedes saber exactamente a qué velocidad está yendo en un momento dado.
Calcular la derivada de funciones puede parecer complicado al principio, pero con un poco de práctica, se convierte en una herramienta poderosa que puedes usar en diversas áreas. Desde la economía hasta la física, las derivadas nos ayudan a entender el mundo que nos rodea de una manera más profunda. Así que la próxima vez que veas una función, recuerda que detrás de ella hay una historia de cambios y tasas que vale la pena explorar.
¿Por qué es importante entender las derivadas?
Entender las derivadas es crucial porque te permite analizar cómo cambian las funciones y, por lo tanto, tomar decisiones informadas en campos como la economía, la ingeniería y la ciencia.
¿Se puede calcular la derivada de funciones más complejas?
¡Absolutamente! Existen muchas reglas y técnicas para calcular derivadas de funciones más complejas, como la regla del producto, la regla del cociente y la regla de la cadena.
¿Qué pasa si la función no es polinómica?
Las derivadas también se pueden calcular para funciones no polinómicas, como las funciones trigonométricas, exponenciales y logarítmicas, usando sus propias reglas específicas.
¿Cuál es la relación entre derivadas y gráficas?
La derivada de una función te ayuda a entender la forma de su gráfica, ya que te indica dónde la función está aumentando, disminuyendo y dónde tiene puntos críticos.
¿Cómo puedo practicar el cálculo de derivadas?
La práctica es clave. Puedes encontrar muchos ejercicios en libros de texto de cálculo, en línea o incluso aplicaciones móviles diseñadas para ayudarte a aprender y practicar derivadas.
¡Y ahí lo tienes! Una guía completa sobre cómo calcular la derivada de 2x. Espero que te haya resultado útil y que te sientas más seguro al abordar el cálculo de derivadas en el futuro. ¡Sigue practicando y divirtiéndote con las matemáticas!