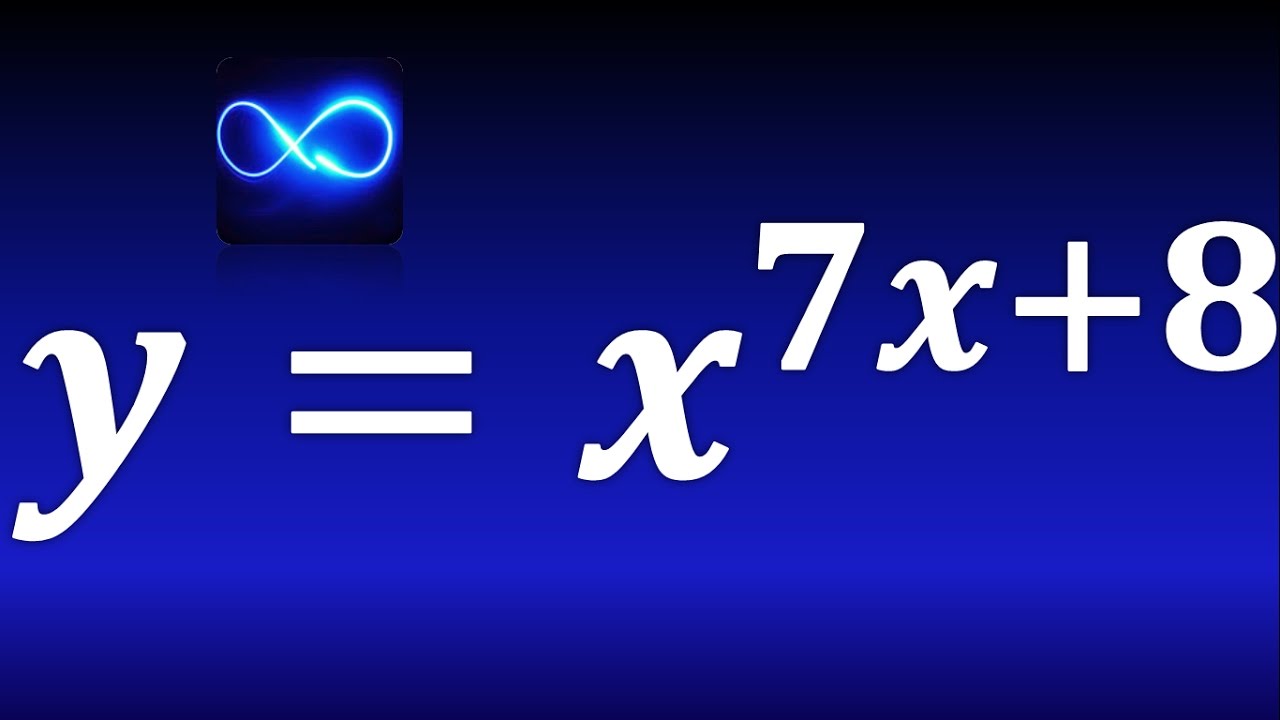¿Alguna vez te has preguntado cómo calcular la derivada de una función que está elevada a otra función? Puede parecer un poco complicado al principio, pero no te preocupes, aquí estamos para desglosarlo paso a paso. Imagina que estás en un laberinto matemático y cada paso que tomas te acerca más a la salida. En este artículo, vamos a explorar el fascinante mundo de las derivadas, específicamente cómo lidiar con esas funciones que se elevan unas a otras. Así que, si estás listo, ¡empecemos este viaje juntos!
¿Qué es una Derivada?
Primero, hablemos un poco sobre qué es una derivada. En términos sencillos, la derivada de una función mide cómo cambia esa función en relación a su variable independiente. Piensa en ello como la velocidad de un coche; si la posición de un coche cambia, la derivada nos dirá qué tan rápido está cambiando esa posición en un instante específico. En matemáticas, esto se traduce en calcular la pendiente de la curva en un punto determinado. Pero, ¿qué pasa cuando tenemos una función elevada a otra función? Aquí es donde se pone interesante.
La Regla de la Cadena
Para calcular la derivada de una función elevada a otra, vamos a necesitar una herramienta poderosa llamada la regla de la cadena. Esta regla es como un atajo en nuestro laberinto. La regla de la cadena nos dice que si tenemos una función compuesta, la derivada de esa función es el producto de la derivada de la función exterior por la derivada de la función interior. ¿Suena complicado? Vamos a desglosarlo un poco más.
Ejemplo de Función Compuesta
Supongamos que tenemos la función y = (f(x))^g(x), donde f(x) y g(x) son funciones diferenciables. Para calcular la derivada dy/dx, aplicamos la regla de la cadena. La derivada se calcularía así:
dy/dx = g(x) * (f(x))^(g(x) - 1) * f'(x) + (f(x))^g(x) * ln(f(x)) * g'(x)¡Vaya! Eso suena complicado, pero vamos a desmenuzarlo paso a paso.
Desglosando la Fórmula
Ahora que tenemos nuestra fórmula, vamos a desglosar cada parte. Primero, tenemos g(x) * (f(x))^(g(x) - 1) * f'(x). Aquí, g(x) es la función que está elevando f(x), y estamos multiplicando por la derivada de f(x), que es f'(x). Luego, tenemos (f(x))^g(x) * ln(f(x)) * g'(x). Esta parte tiene que ver con cómo g(x) afecta a la función f(x). En esencia, estamos considerando cómo cambia g(x) y su impacto en la función general.
Ejemplo Práctico
Ahora, veamos un ejemplo concreto para que todo esto tenga más sentido. Imagina que tienes la función y = (2x + 3)^(x^2). Queremos encontrar la derivada dy/dx. Primero, identificamos nuestras funciones:
f(x) = 2x + 3g(x) = x^2
Ahora, calculemos las derivadas de f(x) y g(x):
f'(x) = 2g'(x) = 2x
Ahora que tenemos todo lo que necesitamos, podemos aplicar la fórmula que discutimos antes. Sustituyendo los valores, obtenemos:
dy/dx = x^2 * (2x + 3)^(x^2 - 1) * 2 + (2x + 3)^(x^2) * ln(2x + 3) * 2xY ahí lo tienes, la derivada de nuestra función elevada a otra función. ¡Fácil, verdad?
Aplicaciones de la Derivada
Las derivadas no son solo un ejercicio académico; tienen aplicaciones en el mundo real. Desde la física hasta la economía, entender cómo cambian las variables puede ayudarte a tomar decisiones informadas. Por ejemplo, en la economía, las empresas utilizan derivadas para maximizar sus beneficios o minimizar costos. En la física, los ingenieros las utilizan para calcular la velocidad y la aceleración de un objeto en movimiento.
Errores Comunes al Calcular Derivadas
Es fácil cometer errores al calcular derivadas, especialmente cuando se trata de funciones compuestas. Aquí hay algunos errores comunes que debes evitar:
- No aplicar la regla de la cadena correctamente: Asegúrate de multiplicar las derivadas de las funciones interior y exterior.
- Olvidar simplificar: Después de calcular la derivada, a veces es fácil olvidar simplificar la expresión final.
- Confundir funciones: Asegúrate de identificar correctamente cuál es la función exterior y cuál es la interior.
Consejos para Mejorar en el Cálculo de Derivadas
Si quieres volverte un experto en derivadas, aquí hay algunos consejos que pueden ayudarte:
- Practica, practica, practica: La mejor manera de mejorar es resolver muchos problemas diferentes.
- Estudia ejemplos: Observa cómo se resuelven otros problemas de derivadas para entender mejor el proceso.
- Usa herramientas visuales: A veces, un gráfico puede ayudarte a entender cómo se comporta una función y su derivada.
Calcular la derivada de una función elevada a otra puede parecer un desafío al principio, pero con práctica y comprensión de las reglas involucradas, se convierte en un proceso mucho más manejable. Recuerda que la clave está en desglosar la función y aplicar la regla de la cadena correctamente. ¡Así que no te desanimes! Cada problema resuelto es un paso más hacia tu maestría en cálculo.
¿Puedo usar la regla de la cadena en otras situaciones además de funciones elevadas a funciones?
¡Absolutamente! La regla de la cadena se aplica en cualquier situación donde tengas una función compuesta, no solo en funciones elevadas a otras funciones.
¿Qué pasa si una de las funciones no es diferenciable?
Si una de las funciones no es diferenciable en el punto en cuestión, entonces no podrás calcular la derivada en ese punto. Es importante asegurarte de que ambas funciones sean diferenciables.
¿Existen calculadoras que pueden ayudar con derivadas complejas?
Sí, hay muchas calculadoras en línea y software matemático que pueden ayudarte a calcular derivadas, pero siempre es bueno entender el proceso detrás de ellas.
¿Cómo puedo verificar mis respuestas al calcular derivadas?
Una buena forma de verificar tus respuestas es graficar la función original y su derivada. Si la derivada es correcta, debería reflejar el comportamiento de la función en términos de aumento y disminución.
¿Cuál es la diferencia entre una derivada y una segunda derivada?
La derivada mide el cambio de una función, mientras que la segunda derivada mide cómo cambia la derivada misma. Esto puede proporcionarte información sobre la concavidad de la función.