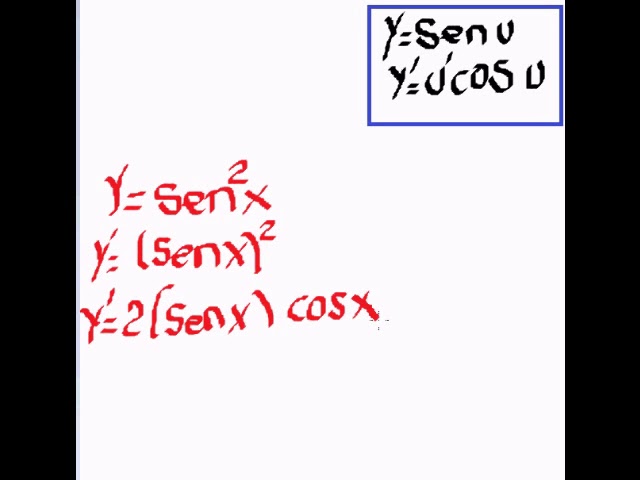Entendiendo la Derivada de Seno Cuadrado
¡Hola! Hoy vamos a desmenuzar un concepto que a muchos les puede parecer complicado: la derivada de seno cuadrado de x, o como se le conoce en notación matemática, sen²(x). Si alguna vez te has preguntado cómo se hace esto, ¡estás en el lugar correcto! Vamos a explorar el proceso paso a paso, desglosando cada parte para que lo entiendas como si estuvieras conversando con un amigo. ¿Listo? ¡Vamos a ello!
¿Qué es una Derivada?
Antes de entrar en materia, es importante que comprendamos qué es una derivada. En términos simples, la derivada mide cómo cambia una función a medida que cambian sus variables. Imagina que estás conduciendo un coche y quieres saber cuán rápido vas en un momento específico. La derivada te da esa información. Así que, en el contexto de sen²(x), queremos saber cómo cambia esta función respecto a x.
¿Por Qué Derivar Seno Cuadrado?
Puede que te estés preguntando: «¿Por qué es importante calcular la derivada de seno cuadrado?» La respuesta es que muchas funciones en matemáticas, física e ingeniería están relacionadas con senos y cosenos. Entender cómo se comportan estas funciones nos ayuda a resolver problemas complejos, como encontrar máximos y mínimos o analizar el movimiento de objetos. Así que, aunque parezca un ejercicio teórico, tiene aplicaciones prácticas muy interesantes.
El Teorema de la Cadena
Ahora que ya tienes una idea de lo que es una derivada, hablemos del Teorema de la Cadena. Este es un concepto crucial cuando se trata de funciones compuestas, como sen²(x). El teorema de la cadena nos dice que si tienes una función dentro de otra, debes derivar la función exterior y luego multiplicarla por la derivada de la función interior. En nuestro caso, la función exterior es el cuadrado y la función interior es seno.
Desglosando la Derivada de sen²(x)
Ahora vamos a aplicar el Teorema de la Cadena a nuestra función. La derivada de sen²(x) se puede escribir como:
f(x) = sen²(x)
Para derivar esto, primero identificamos las funciones interior y exterior:
- Función exterior: u² (donde u = sen(x))
- Función interior: sen(x)
Siguiendo el Teorema de la Cadena, derivamos la función exterior:
f'(x) = 2u * u'
Ahora, sustituimos u por sen(x):
f'(x) = 2sen(x) * (derivada de sen(x))
La derivada de sen(x) es cos(x), así que tenemos:
f'(x) = 2sen(x) * cos(x)
Aplicando la Identidad Trigonométrica
Antes de que te emociones demasiado, hay algo más que puedes hacer con esta derivada. ¿Sabías que hay una identidad trigonométrica que dice que 2sen(x)cos(x) es igual a sen(2x)? Esto significa que podemos simplificar aún más nuestra respuesta. Así que, reescribiendo la derivada:
f'(x) = sen(2x)
¡Y ahí lo tienes! La derivada de sen²(x) es sen(2x). ¿No es genial cómo se puede simplificar tanto?
Ejemplos Prácticos
Vamos a practicar un poco más. Supongamos que quieres calcular la derivada de sen²(π/4). Primero, sustituimos x por π/4 en nuestra derivada:
f'(π/4) = sen(2 * π/4) = sen(π/2) = 1
Así que, la derivada de sen²(x) en x = π/4 es 1. Esto significa que en ese punto, la función está aumentando a una tasa de 1 unidad por cada unidad que aumentas x. ¡Sencillo, verdad?
Derivadas en Contexto
Pero, ¿por qué deberías preocuparte por esto? Bueno, imagina que estás en un parque de diversiones, y quieres saber en qué momento la velocidad de una montaña rusa es máxima. Entender cómo calcular derivadas te permitirá encontrar esos puntos críticos, ayudándote a hacer decisiones más informadas, como dónde sentarte para tener la mejor experiencia.
Errores Comunes al Derivar
A la hora de calcular derivadas, hay algunos errores comunes que vale la pena señalar. Uno de ellos es olvidar aplicar correctamente el Teorema de la Cadena. Asegúrate de identificar las funciones interior y exterior antes de proceder. Otro error frecuente es confundir las derivadas de funciones trigonométricas. Recuerda, la derivada de sen(x) es cos(x), y la de cos(x) es -sen(x).
Ejercicios para Practicar
Ahora que tienes una buena comprensión de cómo calcular la derivada de sen²(x), es hora de practicar. Aquí tienes algunos ejercicios que puedes intentar:
- Calcula la derivada de sen²(x) en x = 0.
- Encuentra la derivada de sen²(x) en x = π/6.
- Calcula la derivada de sen²(x) en x = π/3.
Intenta resolverlos por tu cuenta antes de mirar las respuestas. ¡Es una excelente manera de reforzar lo que has aprendido!
Resumiendo lo Aprendido
Para recapitular, hemos aprendido que la derivada de sen²(x) se puede calcular utilizando el Teorema de la Cadena. Primero identificamos las funciones interior y exterior, derivamos y luego simplificamos usando identidades trigonométricas. Ahora tienes las herramientas necesarias para abordar problemas relacionados con funciones trigonométricas y sus derivadas.
¿Es necesario entender el Teorema de la Cadena para derivar funciones trigonométricas?
¡Definitivamente! El Teorema de la Cadena es fundamental cuando trabajas con funciones compuestas, y las funciones trigonométricas a menudo son compuestas.
¿Puedo usar la regla del producto para derivar sen²(x)?
Sí, también puedes usar la regla del producto. Dado que sen²(x) = sen(x) * sen(x), puedes aplicar la regla del producto y obtendrás el mismo resultado.
¿Qué pasa si quiero derivar otras funciones trigonométricas elevadas al cuadrado?
El proceso es muy similar. Solo asegúrate de identificar correctamente las funciones interior y exterior y aplica el Teorema de la Cadena como lo hicimos aquí.
¿Las derivadas de funciones trigonométricas tienen aplicaciones prácticas?
¡Absolutamente! Las derivadas se utilizan en una variedad de campos, incluyendo física, ingeniería, y economía, para analizar cambios y optimizar resultados.
¿Qué recursos me recomiendas para seguir practicando derivadas?
Existen muchos recursos en línea, desde videos tutoriales hasta plataformas interactivas de matemáticas. Te recomiendo Khan Academy y Wolfram Alpha para practicar y resolver dudas.