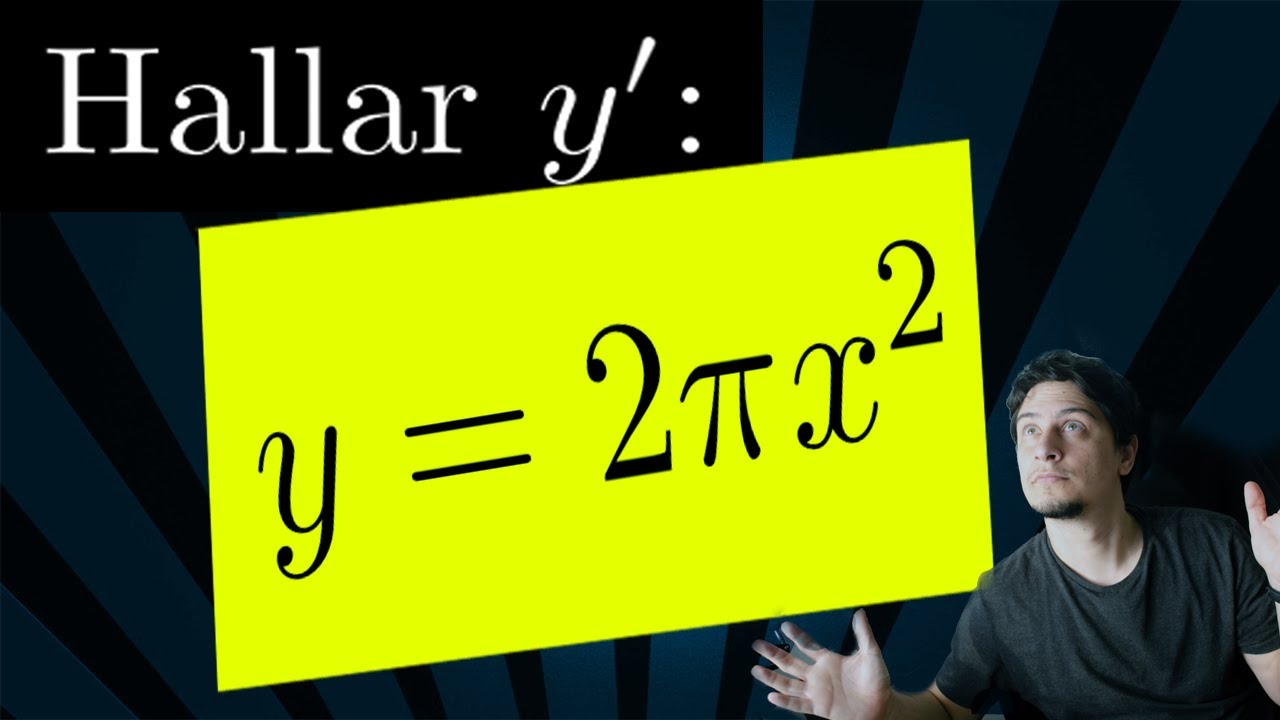¿Alguna vez te has preguntado qué es la derivada de π y por qué debería importarte? La verdad es que la derivada de π, aunque parece un concepto complicado, es una parte fundamental del cálculo y la matemática en general. Pero no te preocupes, aquí estamos para desglosarlo todo de una manera sencilla y amigable. Pi es esa constante mágica que todos conocemos, el número que nos ayuda a entender el mundo de los círculos, pero, ¿qué pasa cuando intentamos aplicar conceptos de cálculo a algo tan «perfecto» como π?
Para empezar, vamos a aclarar qué es una derivada. Imagina que estás conduciendo por una carretera y quieres saber cuán rápido vas en un momento específico. La derivada es precisamente eso: una medida de cómo cambia una función en un punto determinado. Así que, si bien π es una constante, en el contexto del cálculo, podemos explorar su derivada de maneras interesantes. A lo largo de este artículo, vamos a sumergirnos en el mundo de las derivadas, explorando qué significa calcular la derivada de π y algunos ejemplos que te ayudarán a comprender mejor el concepto. ¡Vamos allá!
¿Qué es π y por qué es importante?
Antes de entrar en el tema de la derivada, es fundamental entender qué es π. Este número, aproximadamente igual a 3.14159, es la relación entre la circunferencia de un círculo y su diámetro. Es un número irracional, lo que significa que no se puede expresar como una fracción exacta y sus decimales continúan infinitamente sin repetirse. Pero, ¿por qué es tan crucial en matemáticas y ciencias?
La importancia de π radica en su omnipresencia en diferentes áreas de la matemática, desde la geometría hasta el análisis y más allá. Se utiliza en fórmulas para calcular áreas y volúmenes de figuras geométricas, en ecuaciones de ondas y en la teoría de probabilidades, por mencionar solo algunas aplicaciones. Sin π, muchas de las matemáticas que usamos a diario simplemente no tendrían sentido. Es como el pegamento que une varios conceptos matemáticos y científicos.
¿Qué es una derivada?
Ahora que tenemos claro qué es π, hablemos de derivadas. La derivada de una función en un punto específico nos da la pendiente de la tangente a la curva en ese punto. En términos más simples, es la tasa de cambio instantánea. Por ejemplo, si estás en una montaña rusa, la derivada te diría cuán empinada es la subida o la bajada en un momento particular. ¿Te imaginas estar en la cima de una montaña rusa y no saber qué tan rápido te estás moviendo hacia abajo? Eso es lo que hace la derivada: te da esa información vital.
La Notación de la Derivada
Cuando hablamos de derivadas, nos encontramos con varias notaciones. La más común es f'(x), que representa la derivada de la función f en relación a x. También puedes ver la notación de Leibniz, que es (frac{dy}{dx}), donde y es la función y x es la variable independiente. Ambas notaciones son herramientas útiles para comunicarnos en el mundo del cálculo.
¿Cómo se relaciona π con las derivadas?
Aquí es donde se pone interesante. Aunque π es una constante, podemos hablar de la derivada de funciones que involucran a π. Por ejemplo, consideremos la función f(x) = πx. Si tomamos la derivada de esta función, f'(x) = π, lo que significa que la pendiente de la línea en cualquier punto de esta función es constante y siempre igual a π. Es como si estuvieras empujando un carrito de compras en línea recta; la velocidad a la que empujas (la derivada) es constante.
Ejemplo Práctico: Derivada de una Función que Involucra π
Imaginemos que tenemos una función más compleja, como f(x) = πx^2. Aquí, la derivada sería f'(x) = 2πx. ¿Qué significa esto? La tasa de cambio de la función f(x) no es constante; depende de x. A medida que x aumenta, la pendiente de la tangente también aumenta. Piensa en una pista de patinaje: si estás patinando en un círculo, a medida que te alejas del centro, tu velocidad cambia, y eso es lo que representa esta derivada.
Aplicaciones de la Derivada de Funciones que Involucran π
Ahora que hemos visto cómo calcular la derivada de funciones que involucran a π, es hora de explorar algunas aplicaciones. ¿Sabías que las derivadas tienen un papel crucial en la optimización? Imagina que estás diseñando una pista de atletismo circular y quieres maximizar el área. La derivada te ayudará a encontrar los puntos donde el área es máxima o mínima, lo que es vital para cualquier diseño eficiente.
Optimización en el Mundo Real
Volviendo a nuestra pista de atletismo, supongamos que la longitud de la pista es fija, y deseas maximizar el área. Aquí, podrías usar la derivada para encontrar el radio óptimo que maximiza el área del círculo. La relación entre la longitud de la pista y el radio está directamente relacionada con π, y al calcular la derivada, podrías determinar el radio ideal para tus atletas. Este tipo de análisis no solo es útil en deportes, sino también en arquitectura, ingeniería y economía.
La Derivada en Otras Funciones Trigonométricas
¿Pero qué hay de las funciones trigonométricas que también involucran a π? Pensemos en la función seno, que está íntimamente relacionada con π. La derivada de f(x) = sin(πx) es f'(x) = π cos(πx). Aquí, la derivada nos dice cómo cambia el valor del seno en relación con el cambio en x, multiplicado por π. Esto nos da una nueva perspectiva sobre cómo π se manifiesta en las funciones trigonométricas.
Aplicaciones de la Derivada en Trigonometría
Las derivadas de funciones trigonométricas son esenciales en campos como la ingeniería y la física. Por ejemplo, en la ingeniería de señales, comprender cómo cambian las ondas sinusoidales en relación con el tiempo es crucial. La derivada te permite analizar frecuencias, amplitudes y otros parámetros que son vitales para el diseño de circuitos y sistemas de comunicación. Así que, aunque π puede parecer solo un número, su presencia en estas funciones tiene un impacto real y significativo en nuestra vida diaria.
1. ¿Se puede calcular la derivada de π como una constante?
No, porque π es una constante, su derivada es cero. Sin embargo, puedes calcular la derivada de funciones que incluyen π, como hemos visto anteriormente.
2. ¿Por qué es importante entender la derivada de funciones que involucran π?
Entender cómo π se relaciona con las derivadas te ayuda a aplicar conceptos matemáticos en situaciones del mundo real, desde optimización hasta análisis de señales.
3. ¿Cómo se aplica la derivada en la vida cotidiana?
Las derivadas se utilizan en una variedad de campos, incluyendo economía para maximizar beneficios, en física para analizar el movimiento y en ingeniería para diseñar estructuras eficientes.
4. ¿Qué otros conceptos matemáticos están relacionados con π?
Además de las derivadas, π está relacionado con integrales, series infinitas, y tiene aplicaciones en estadística y teoría de números.
5. ¿Es necesario saber cálculo para entender la importancia de π?
No es estrictamente necesario, pero tener una comprensión básica de cálculo puede ayudarte a apreciar cómo π se utiliza en diferentes contextos matemáticos y científicos.
En conclusión, la derivada de π, aunque simple en su forma, abre la puerta a un mundo de posibilidades en la matemática y sus aplicaciones. Así que, la próxima vez que escuches sobre π, recuerda que hay mucho más detrás de este número que solo su valor constante.