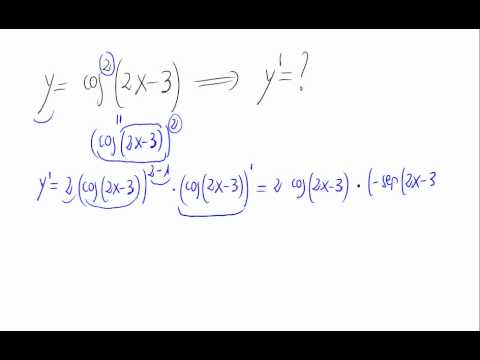¿Alguna vez te has preguntado cómo se calcula la derivada de una función trigonométrica como el coseno cuadrado? Si la respuesta es sí, ¡estás en el lugar correcto! En esta guía, vamos a desglosar paso a paso cómo derivar la función cos^2(x), una habilidad esencial para cualquier estudiante de cálculo. Pero no te preocupes, no vamos a usar un lenguaje complicado. Más bien, lo haremos de manera que hasta tu amigo que odia las matemáticas pueda entenderlo. Así que, siéntate, relájate y vamos a sumergirnos en el fascinante mundo de las derivadas.
¿Qué es la Derivada?
Antes de entrar en materia, es importante entender qué es una derivada. En términos simples, la derivada mide cómo cambia una función en relación a su variable. Imagina que estás conduciendo un coche y quieres saber a qué velocidad vas en un instante específico. La derivada es como ese velocímetro: te dice la velocidad en un momento dado. En el caso de la función cos^2(x), lo que queremos saber es cómo cambia esta función cuando hacemos pequeños cambios en x.
La Regla de la Cadena
Para derivar cos^2(x), utilizaremos una herramienta poderosa llamada la regla de la cadena. Esta regla es esencial cuando trabajamos con funciones compuestas. ¿Recuerdas cómo al hacer una lasaña, tienes que cocinar cada capa por separado antes de unirlas? La regla de la cadena es como eso: nos permite derivar cada parte de la función por separado antes de juntar los resultados.
Aplicando la Regla de la Cadena
Ahora, para aplicar la regla de la cadena a cos^2(x), primero identificamos las funciones dentro de la función. Aquí, tenemos una función externa que es u^2 (donde u = cos(x)) y una función interna que es cos(x). Así que, la derivada de cos^2(x) se puede escribir como:
f'(x) = 2u * u'Donde u' = -sin(x), que es la derivada de cos(x). Al juntar todo, obtenemos:
f'(x) = 2cos(x)(-sin(x)) = -2cos(x)sin(x)Ejemplo Práctico: Derivando Coseno Cuadrado
Ahora que tenemos la fórmula, veamos un ejemplo práctico. Supongamos que queremos calcular la derivada de cos^2(π/4). Primero, calculamos el valor de cos(π/4), que es √2/2. Ahora, usando nuestra derivada:
f'(π/4) = -2(√2/2)(sin(π/4))Como sin(π/4) también es √2/2, sustituimos y simplificamos:
f'(π/4) = -2(√2/2)(√2/2) = -2(1/2) = -1Así que la derivada de cos^2(x) en x = π/4 es -1. ¡Fácil, verdad?
Visualizando la Derivada
Ahora que hemos calculado la derivada, es interesante pensar en lo que esto significa gráficamente. La derivada -1 indica que en x = π/4, la pendiente de la tangente a la curva de cos^2(x) es negativa. Esto significa que la función está disminuyendo en ese punto. Imagina que estás en una montaña rusa: cuando la pendiente es negativa, ¡es como descender por una caída emocionante!
Propiedades de la Derivada de Coseno Cuadrado
Entender las propiedades de la derivada de cos^2(x) puede ayudarte a aplicar este conocimiento en diferentes situaciones. Aquí hay algunas propiedades clave:
Comportamiento Periódico
La función cos^2(x) es periódica, lo que significa que su comportamiento se repite cada 2π. Esto se traduce a que la derivada también seguirá un patrón. Así que, si encuentras la derivada en un punto, puedes predecir su comportamiento en otros puntos de la función.
Máximos y Mínimos Locales
La derivada nos ayuda a identificar máximos y mínimos locales. Cuando la derivada es igual a cero, puede indicar un punto donde la función alcanza un máximo o mínimo. Al observar el gráfico de cos^2(x), verás que alterna entre máximos y mínimos a medida que x avanza. Esto es crucial para optimizar funciones en problemas de la vida real, como maximizar ganancias o minimizar costos.
Aplicaciones en Física y Ingeniería
Las derivadas de funciones trigonométricas, como cos^2(x), tienen aplicaciones en diversos campos, incluyendo la física y la ingeniería. Por ejemplo, al analizar el movimiento de un péndulo o el comportamiento de circuitos eléctricos, las derivadas nos ayudan a entender cómo cambian las variables con el tiempo.
Ejercicios para Practicar
Para asegurarte de que has comprendido el concepto, aquí tienes algunos ejercicios para practicar:
- Calcula la derivada de
cos^2(2x). - Encuentra la derivada de
cos^2(x + π/3). - Determina el valor de la derivada en
x = 0yx = π/2.
¿Por qué es importante aprender a derivar funciones trigonométricas?
Las funciones trigonométricas son fundamentales en matemáticas y ciencias aplicadas. Aprender a derivarlas te permite resolver problemas complejos en física, ingeniería y otros campos.
¿Qué otras funciones debo aprender a derivar?
Además de cos^2(x), es útil conocer cómo derivar funciones como sin(x), tan(x) y combinaciones de estas funciones. Cuanto más practiques, más fácil será.
¿Existen reglas adicionales para derivadas que debería conocer?
Sí, además de la regla de la cadena, existen otras como la regla del producto y la regla del cociente. Cada una tiene su propia aplicación y es útil conocerlas para derivar una variedad de funciones.
¿Puedo usar una calculadora para encontrar derivadas?
Claro, muchas calculadoras científicas y software matemático pueden calcular derivadas. Sin embargo, es importante entender el proceso manualmente para desarrollar una comprensión más profunda de las matemáticas.
En resumen, la derivada de cos^2(x) no es solo un ejercicio académico; es una herramienta poderosa que se utiliza en muchas disciplinas. Así que, la próxima vez que te encuentres ante una función trigonométrica, recuerda que tienes las herramientas para desglosarla y entenderla mejor. ¡Sigue practicando y verás cómo te conviertes en un experto en derivadas!