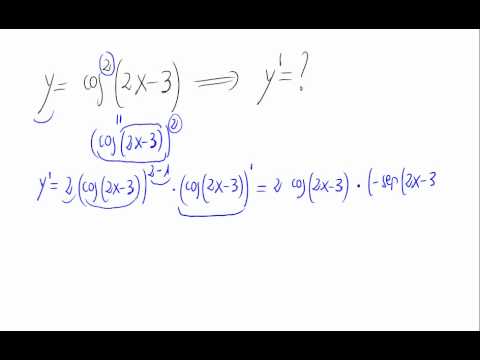¿Te has encontrado alguna vez con la necesidad de derivar funciones trigonométricas y te ha parecido un verdadero rompecabezas? ¡No te preocupes! Hoy vamos a desmenuzar el concepto de la derivada de coseno al cuadrado, una función que a menudo aparece en el mundo de las matemáticas y la física. No solo exploraremos cómo calcularla, sino que también te proporcionaré ejemplos prácticos para que puedas entenderlo mejor. ¡Así que prepárate para sumergirte en el fascinante mundo de las derivadas!
¿Qué es la Derivada?
Antes de entrar de lleno en la derivada de coseno al cuadrado, es crucial que entendamos qué es una derivada. Imagina que estás conduciendo un coche y quieres saber qué tan rápido vas en un momento específico. La derivada es precisamente eso: la tasa de cambio de una función en un punto determinado. En términos más técnicos, es el límite de la razón de cambio de una función cuando el intervalo de tiempo se acerca a cero. ¡Sencillo, verdad?
La Función Coseno al Cuadrado
Ahora que tenemos una idea clara de qué es una derivada, pasemos a la función que nos interesa: el coseno al cuadrado, o cos^2(x). Esta función es el resultado de elevar el coseno de un ángulo al cuadrado. Si alguna vez has dibujado un círculo unitario, te habrás dado cuenta de que el coseno representa la coordenada x de un punto en la circunferencia. Ahora, al elevarlo al cuadrado, simplemente estamos tomando el valor de x y multiplicándolo por sí mismo. ¡Pero espera! ¿Qué pasa cuando queremos encontrar su derivada?
Regla de la Cadena: El Secreto Detrás de la Derivada de Coseno al Cuadrado
Para derivar cos^2(x), vamos a utilizar una herramienta fundamental en cálculo llamada la regla de la cadena. Esta regla es esencial cuando tenemos funciones compuestas, y en este caso, cos^2(x) se puede ver como una función externa u^2 donde u = cos(x). Así que, siguiendo la regla de la cadena, la derivada se calcula como sigue:
Derivada de la Función Compuesta
La derivada de u^2 es 2u, y luego multiplicamos por la derivada de u>, que es -sin(x). Por lo tanto, la derivada de cos^2(x) es:
d/dx[cos^2(x)] = 2cos(x)(-sin(x)) = -2cos(x)sin(x)
¿Ves cómo todo se conecta? Este resultado es clave para entender cómo se comporta la función cos^2(x) a medida que cambiamos el valor de x.
Ejemplos Prácticos de Derivadas
Ahora que tenemos la fórmula, es hora de ponerla en práctica. Vamos a explorar algunos ejemplos que te ayudarán a solidificar este conocimiento.
Ejemplo 1: Derivada en un Punto Específico
Supongamos que queremos encontrar la derivada de cos^2(x) en x = π/4. Primero, calculemos cos(π/4), que es √2/2. Luego, usando nuestra derivada, sustituimos:
-2cos(π/4)sin(π/4) = -2(√2/2)(√2/2) = -2(1/2) = -1
Así que la derivada en ese punto es -1. ¡Fácil, verdad?
Ejemplo 2: Derivada en un Rango de Valores
Ahora, ¿qué tal si queremos ver cómo se comporta la derivada de cos^2(x) en un rango de valores, digamos de 0 a 2π? Podemos graficar la función original y su derivada. Al hacerlo, notamos que la derivada oscila entre -1 y 0, lo que indica que la función cos^2(x) está disminuyendo en ciertos intervalos y aumentando en otros. ¡Es como ver una montaña rusa matemática!
Aplicaciones de la Derivada de Coseno al Cuadrado
Ahora que hemos cubierto la teoría y algunos ejemplos, hablemos de por qué esto es importante. Las derivadas de funciones trigonométricas, como cos^2(x), tienen aplicaciones en diversas áreas como la física, la ingeniería y la economía. Por ejemplo, en física, al analizar el movimiento de un objeto en un plano, es crucial entender cómo cambian las fuerzas en función del tiempo. La derivada nos ayuda a modelar esos cambios.
Resumiendo lo Aprendido
Así que, para recapitular, hemos aprendido que la derivada de cos^2(x) se obtiene usando la regla de la cadena y que su resultado es -2cos(x)sin(x). Además, hemos visto ejemplos que ilustran cómo calcular la derivada en puntos específicos y en rangos de valores. Y lo más importante, hemos explorado las aplicaciones de esta derivada en el mundo real. Ahora que tienes este conocimiento en tu bolsillo, ¡seguro que te sentirás más confiado a la hora de enfrentarte a problemas de cálculo!
¿Por qué se usa la regla de la cadena para derivar cos^2(x)?
La regla de la cadena se usa porque cos^2(x) es una función compuesta. Primero derivamos la función exterior y luego multiplicamos por la derivada de la función interior.
¿Hay alguna forma de simplificar -2cos(x)sin(x)?
Sí, se puede simplificar usando la identidad trigonométrica sin(2x) = 2sin(x)cos(x), por lo que -2cos(x)sin(x) = -sin(2x).
¿En qué situaciones prácticas se necesita la derivada de cos^2(x)?
Las derivadas de funciones trigonométricas son esenciales en la física para analizar el movimiento y en la ingeniería para optimizar diseños. También son útiles en economía para entender tasas de cambio.
¿La derivada de cos^2(x) siempre será negativa?
No necesariamente. La derivada puede ser positiva, negativa o cero dependiendo del intervalo de x que estemos considerando.
¿Existen otras funciones trigonométricas que se puedan derivar de manera similar?
¡Absolutamente! Funciones como sin^2(x), tan(x), y muchas otras se pueden derivar usando técnicas similares. Cada una tiene su propia fórmula, pero la regla de la cadena es una herramienta común en todos los casos.