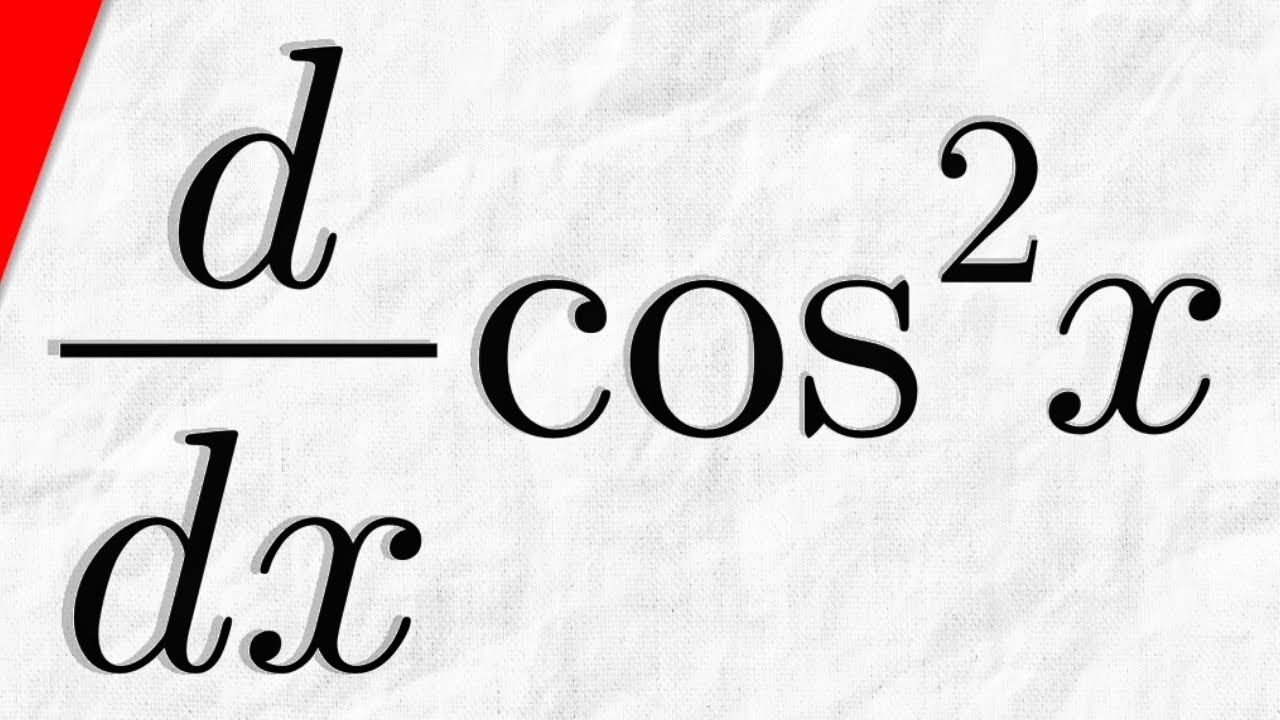¿Te has encontrado alguna vez en la situación de tener que calcular la derivada de una función trigonométrica y no saber por dónde empezar? ¡No te preocupes! Hoy vamos a desglosar este tema de una manera sencilla y accesible. En este artículo, nos enfocaremos en cómo calcular la derivada de la función cos(2x). La derivada es una herramienta fundamental en el cálculo que nos ayuda a entender cómo cambia una función en relación con su variable. Así que, si te sientes un poco perdido, quédate conmigo y vamos a hacerlo paso a paso.
¿Qué es una Derivada?
Antes de meternos de lleno en la derivada de cos(2x), es importante entender qué es una derivada. En términos simples, la derivada de una función nos dice la tasa de cambio de esa función en un punto dado. Piensa en ello como si estuvieras conduciendo un coche: la velocidad a la que te mueves es la derivada de tu posición con respecto al tiempo. Cuanto más rápido vayas, mayor será tu derivada.
Las Funciones Trigonométricas y sus Derivadas
Las funciones trigonométricas, como seno y coseno, tienen derivadas bien definidas. Para el coseno, la regla básica es que la derivada de cos(x) es -sin(x). Pero, cuando estamos tratando con funciones compuestas, como cos(2x), necesitamos aplicar una técnica adicional llamada la regla de la cadena. Esto es lo que hace que calcular derivadas de funciones más complejas sea tan interesante.
La Regla de la Cadena
La regla de la cadena es como un atajo que nos permite calcular la derivada de una función compuesta. Imagina que tienes una caja dentro de otra caja. Para abrir la caja exterior, primero necesitas abrir la interior. En términos de cálculo, esto significa que si tienes una función compuesta, primero derivarás la función exterior y luego multiplicarás por la derivada de la función interior.
Calcular la Derivada de cos(2x)
Ahora que hemos cubierto los conceptos básicos, ¡vamos a calcular la derivada de cos(2x) paso a paso! Sigamos el proceso juntos.
Paso 1: Identificar las Funciones
La función que estamos tratando es cos(2x). Aquí, la función exterior es cos(u) y la función interior es u = 2x. Necesitamos encontrar la derivada de ambas partes.
Paso 2: Derivar la Función Exterior
Como mencionamos antes, la derivada de cos(u) es -sin(u). Así que, en este caso, la derivada de cos(2x) respecto a u es -sin(2x).
Paso 3: Derivar la Función Interior
Ahora, derivamos la función interior, que es 2x. La derivada de 2x es simplemente 2. Aquí es donde la regla de la cadena entra en juego: multiplicamos la derivada de la función exterior por la derivada de la función interior.
Paso 4: Aplicar la Regla de la Cadena
Por lo tanto, al aplicar la regla de la cadena, tenemos:
f'(x) = -sin(2x) * 2
Lo que se simplifica a:
f'(x) = -2sin(2x)
Ejemplos Prácticos
Ahora que hemos derivado cos(2x), veamos algunos ejemplos prácticos para consolidar este conocimiento. Imagina que estamos trabajando en un problema de física donde necesitamos encontrar la tasa de cambio de la posición de un objeto en movimiento circular. La función que describe la posición podría ser algo como cos(2x), donde x representa el tiempo.
Ejemplo 1: Aplicación en Movimiento Circular
Supón que la posición de un objeto en movimiento circular está dada por la función cos(2x). Si quieres saber cómo cambia la posición en un instante específico, simplemente sustituyes ese valor en la derivada que encontramos. Por ejemplo, si x = π/4, entonces:
f'(π/4) = -2sin(2 * π/4) = -2sin(π/2) = -2 * 1 = -2
Esto significa que en ese instante, el objeto está retrocediendo a una velocidad de 2 unidades por segundo.
Ejemplo 2: Gráficas y Comportamiento
Otra forma de visualizar lo que hemos aprendido es a través de gráficas. Al graficar la función cos(2x) y su derivada -2sin(2x), puedes ver cómo la derivada indica los puntos donde la función cambia de dirección. Cuando la derivada es cero, la función tiene un máximo o mínimo. Es fascinante observar cómo las matemáticas y la visualización se entrelazan, ¿verdad?
Consejos para Practicar Derivadas de Funciones Trigonométricas
Ahora que tienes una idea clara de cómo calcular la derivada de cos(2x), aquí hay algunos consejos que te ayudarán a practicar y mejorar tus habilidades:
- Practica con diferentes funciones: No te limites solo a cos(2x). Intenta derivar funciones como sin(3x) o tan(4x) para familiarizarte con diferentes escenarios.
- Usa recursos en línea: Hay muchas calculadoras y herramientas en línea que pueden ayudarte a verificar tus respuestas. Esto es útil para aprender de tus errores.
- Haz ejercicios a mano: Aunque las herramientas digitales son útiles, practicar a mano te ayudará a comprender mejor el proceso.
¿Cuál es la derivada de cos(x)?
La derivada de cos(x) es -sin(x). Esta es una regla básica en cálculo que es fundamental para cualquier estudiante.
¿Qué es la regla de la cadena en cálculo?
La regla de la cadena es una técnica que se utiliza para derivar funciones compuestas. Te permite calcular la derivada de una función exterior multiplicada por la derivada de la función interior.
¿Por qué es importante la derivada en matemáticas y física?
La derivada es crucial porque nos proporciona información sobre la tasa de cambio. En física, por ejemplo, nos ayuda a entender cómo varían la posición y la velocidad de un objeto a lo largo del tiempo.
¿Cómo puedo mejorar mis habilidades en cálculo?
La práctica constante es clave. Resuelve problemas, estudia diferentes tipos de funciones y busca recursos adicionales como videos y libros de texto. No dudes en pedir ayuda si te sientes atascado.
Así que ahí lo tienes, una guía completa para calcular la derivada de cos(2x). Recuerda que la práctica hace al maestro, así que sigue practicando y no dudes en explorar más sobre las maravillas del cálculo. ¡Buena suerte!