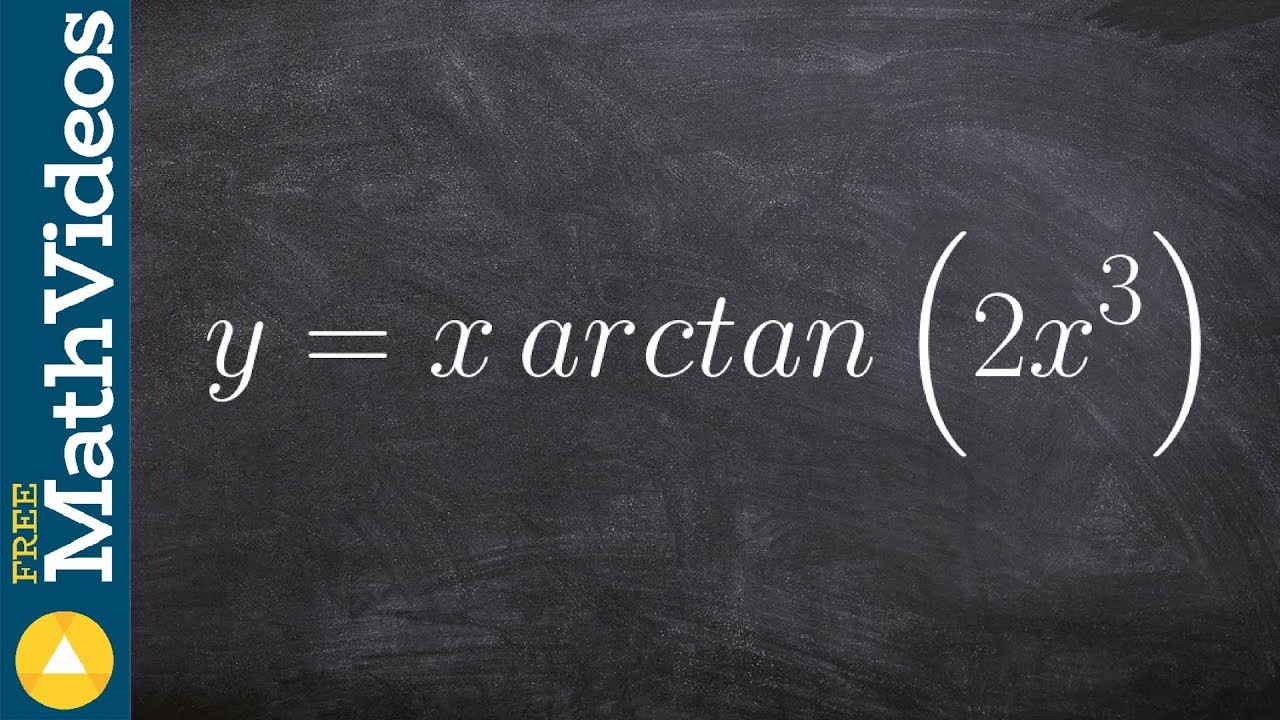¿Alguna vez te has preguntado cómo se comportan las funciones trigonométricas inversas en el mundo del cálculo? Bueno, ¡estás en el lugar correcto! Hoy vamos a sumergirnos en el fascinante mundo de la derivada de la función arctangente, comúnmente abreviada como arctan. Esta función, que se usa en diversas áreas como la ingeniería, la física y las matemáticas, puede parecer un poco intimidante al principio, pero te prometo que desglosándola paso a paso, te resultará mucho más accesible. ¿Listo para desentrañar este misterio?
La función arctan es la inversa de la tangente y se utiliza para determinar el ángulo cuyas tangentes son iguales a un número dado. Es decir, si tienes un número y quieres saber a qué ángulo corresponde, arctan es tu mejor amigo. Pero, ¿qué hay de su derivada? Aquí es donde las cosas se ponen interesantes. La derivada de arctan(x) es una de las más sencillas de calcular, y entender su significado y aplicaciones puede abrirte muchas puertas en el estudio del cálculo y más allá.
¿Qué es la Derivada y por Qué es Importante?
Antes de entrar en la derivada de arctan, tomemos un momento para hablar sobre qué es una derivada. En términos simples, la derivada de una función en un punto dado mide cómo cambia el valor de la función cuando se hace un pequeño cambio en su entrada. Piensa en ello como la pendiente de la curva en ese punto. Si te imaginas conduciendo un coche, la derivada te diría cuán rápido estás acelerando o frenando en un instante particular.
Entonces, ¿por qué es tan crucial entender las derivadas? Porque nos permiten analizar el comportamiento de las funciones, encontrar máximos y mínimos, y resolver problemas en física, economía y muchas otras disciplinas. Ahora, volviendo a la arctan, la derivada de esta función se convierte en una herramienta poderosa cuando trabajamos con ángulos y triángulos, especialmente en problemas relacionados con la geometría y la trigonometría.
Derivada de Arctan: Fórmula y Cálculo
Ahora que tenemos una buena base, hablemos de la derivada de arctan(x). La fórmula es bastante sencilla:
La derivada de arctan(x) es:
f'(x) = 1 / (1 + x²)
Esto significa que, para cualquier valor de x que elijas, puedes calcular la tasa de cambio de arctan en ese punto usando esta fórmula. Pero, ¿cómo llegamos a esta fórmula? Para entenderlo mejor, echemos un vistazo a cómo se deriva.
Derivación usando la Regla de la Cadena
Una forma de derivar arctan(x) es usando la regla de la cadena. La idea es que si sabemos cómo derivar la función tangente, podemos usar esa información para obtener la derivada de su inversa. Comencemos recordando que si y = arctan(x), entonces x = tan(y).
Si aplicamos la derivada implícita, obtenemos:
1 = sec²(y) * dy/dx
Sabiendo que sec²(y) = 1 + tan²(y), podemos sustituir tan(y) por x, lo que nos lleva a:
dy/dx = 1 / (1 + x²)
¡Y ahí lo tienes! Una derivada clara y concisa que puedes utilizar en tus cálculos.
Interpretación Gráfica de la Derivada de Arctan
Ahora que tenemos la fórmula, es útil visualizar lo que significa. La función arctan(x) tiene una forma característica que se asemeja a una S estirada. Su derivada, 1 / (1 + x²), nos dice cómo cambia la pendiente de la curva en diferentes puntos.
Si observamos el gráfico de arctan(x), notaremos que a medida que x se aleja de cero, la pendiente se va acercando a cero. Esto significa que la función se aplana a medida que se aproxima a sus asíntotas horizontales en y = π/2 y y = -π/2. La derivada nos ayuda a entender que, aunque la función sigue aumentando, lo hace a un ritmo cada vez más lento.
Aplicaciones Prácticas de la Derivada de Arctan
Las aplicaciones de la derivada de arctan son numerosas. Una de las más comunes se encuentra en la física, especialmente en el análisis de movimientos. Por ejemplo, si estás trabajando con un objeto que se mueve en un plano inclinado, la derivada de arctan puede ayudarte a determinar el ángulo de inclinación en relación con la aceleración del objeto.
También se utiliza en la economía para analizar tasas de crecimiento y cambios en la oferta y la demanda. En ingeniería, se aplica en el diseño de circuitos y en la modelación de sistemas de control. En resumen, la derivada de arctan no es solo una fórmula en un libro de texto; es una herramienta esencial en el mundo real.
Ejemplos de Cálculo de Derivadas de Arctan
Para asegurarnos de que realmente entiendes cómo aplicar la derivada de arctan, veamos algunos ejemplos prácticos.
Ejemplo 1: Cálculo de la Derivada en un Punto Específico
Supongamos que queremos calcular la derivada de arctan(x) en x = 1. Usamos la fórmula:
f'(1) = 1 / (1 + 1²) = 1 / 2 = 0.5
Esto significa que en x = 1, la pendiente de la curva de arctan es 0.5. Si lo visualizas, esto indica que la función está aumentando, pero no tan rápidamente.
Ejemplo 2: Aplicación en un Problema de Física
Imagina que tienes un objeto que se desliza por un plano inclinado. Si el ángulo de inclinación está relacionado con la tangente de la altura y la base del triángulo formado, podrías usar arctan para determinar el ángulo. Supón que la altura es 3 y la base es 4. Entonces:
θ = arctan(3/4)
Si necesitas la derivada en este punto, simplemente calcularías f'(3/4) usando la misma fórmula, lo que te permitirá entender cómo varía la inclinación en función de la altura.
Más Allá de la Derivada: Integración de Arctan
Aparte de las derivadas, es interesante mencionar que la función arctan también tiene una relación con la integración. La integral de 1 / (1 + x²) es precisamente arctan(x) + C, donde C es la constante de integración. Esto es útil si alguna vez necesitas revertir el proceso y encontrar el área bajo la curva de la función.
A lo largo de este artículo, hemos explorado la derivada de arctan desde sus fundamentos hasta sus aplicaciones prácticas. La fórmula es simple, pero su importancia es profunda. Desde entender cómo cambian las funciones hasta aplicarla en problemas del mundo real, la derivada de arctan es una herramienta valiosa en tu arsenal matemático.
Si te ha parecido interesante todo esto, ¡te animo a seguir practicando y explorando más sobre el cálculo y sus aplicaciones! Recuerda, cada nuevo concepto que aprendes es un ladrillo más en la construcción de tu conocimiento.
1. ¿Qué significa la derivada de arctan en términos prácticos?
La derivada de arctan nos indica cómo cambia el ángulo en relación con la tangente a medida que modificamos el valor de x. Es útil en contextos como la física y la ingeniería.
2. ¿La derivada de arctan(x) es siempre positiva?
Sí, la derivada de arctan(x) es siempre positiva, lo que significa que la función arctan(x) siempre está aumentando, aunque a un ritmo cada vez más lento.
3. ¿Cómo puedo practicar la derivada de arctan?
Una buena forma de practicar es resolver problemas que involucren la derivada de arctan en contextos reales, como en problemas de movimiento o en el análisis de gráficos.
4. ¿Qué otras funciones trigonométricas inversas tienen derivadas simples?
Además de arctan, las funciones arcsin y arccos también tienen derivadas que se pueden calcular fácilmente, y son útiles en diferentes contextos.
5. ¿Cuál es la importancia de la función arctan en la vida cotidiana?
La función arctan se utiliza en diversas aplicaciones cotidianas, como en la navegación, la construcción, y en el diseño de gráficos y modelos en computación.