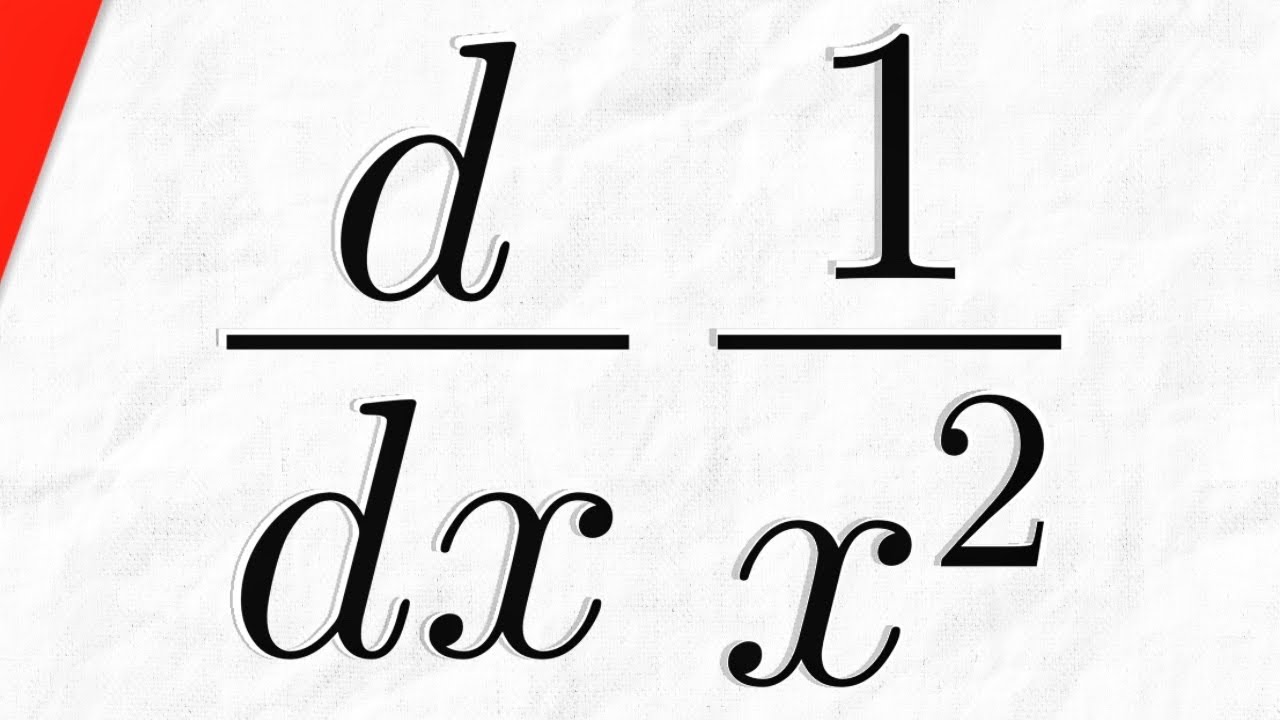¿Alguna vez te has preguntado cómo funcionan las tasas de cambio en el mundo real? Imagina que estás en un parque de diversiones, montando una montaña rusa. La velocidad con la que subes y bajas puede cambiar en un instante, y eso es precisamente lo que las derivadas nos ayudan a entender. En este artículo, vamos a desglosar el proceso de calcular la derivada de una función simple como 1 x 2, un ejercicio que, aunque parece básico, nos servirá para entender conceptos más complejos en el futuro. Así que, siéntate cómodo y acompáñame en este viaje por el mundo de las matemáticas.
¿Qué es una Derivada?
Para comenzar, es crucial entender qué es una derivada. En términos sencillos, la derivada de una función en un punto específico nos dice la pendiente de la tangente a la curva en ese punto. Imagina que estás dibujando una línea que toca la curva en solo un punto. Esa línea es la tangente, y su inclinación es lo que llamamos la derivada. En otras palabras, la derivada nos dice cómo cambia una función a medida que cambiamos su entrada. ¡Es como tener un radar que te dice qué tan rápido va algo en un momento dado!
Derivadas en la Práctica: El Caso de 1 x 2
Ahora, centrémonos en nuestro ejemplo: calcular la derivada de 1 x 2. Este es un caso muy sencillo, pero es fundamental para entender cómo funcionan las derivadas en general. Aquí, 1 x 2 es simplemente una constante, es decir, no cambia con respecto a ninguna variable.
Identificando la Constante
Cuando hablamos de derivadas, es importante identificar si estamos tratando con una constante o una función variable. En nuestro caso, 1 x 2 es igual a 2. Así que, si tomamos la derivada de una constante, como 2, la respuesta siempre será cero. Esto se debe a que no hay ningún cambio en la función: no importa cuánto cambies la variable, el resultado sigue siendo el mismo.
Regla de la Derivada de una Constante
La regla de la derivada de una constante dice que si f(x) = c, donde c es una constante, entonces f'(x) = 0. Esto se puede pensar como un coche que va a una velocidad constante. No importa cuánto tiempo pase, la velocidad no cambia. Así que, al final del día, la derivada de 1 x 2 es simplemente 0.
Pasos para Calcular Derivadas
Ahora que hemos establecido cómo calcular la derivada de una constante, vamos a ampliar nuestros horizontes. Aprender a calcular derivadas de funciones más complejas puede ser emocionante. Aquí hay algunos pasos básicos que puedes seguir:
Identificar la Función
Antes de hacer cualquier cálculo, necesitas saber qué función estás trabajando. ¿Es una constante, una función lineal, cuadrática o algo más complicado? En nuestro caso, empezamos con una constante: 2.
Aplicar las Reglas de Derivación
Dependiendo de la naturaleza de la función, necesitarás aplicar diferentes reglas. Algunas de las más comunes incluyen:
– Regla de la potencia: Si tienes x^n, entonces la derivada es n*x^(n-1).
– Regla del producto: Para dos funciones u y v, la derivada es u’v + uv’.
– Regla del cociente: Para funciones u y v, la derivada es (u’v – uv’) / v^2.
Simplificar la Respuesta
Después de aplicar las reglas, asegúrate de simplificar tu respuesta. Esto hará que sea más fácil entender y utilizar en el futuro.
Ejemplo Práctico: Funciones Más Complejas
Para ilustrar estos pasos, consideremos una función más compleja: f(x) = 3x^2 + 5x + 2. Sigamos los pasos:
Identificando la Función
Aquí, nuestra función es un polinomio, que es más interesante que una simple constante.
Aplicando la Regla de la Potencia
Para calcular la derivada, aplicamos la regla de la potencia a cada término:
– La derivada de 3x^2 es 6x.
– La derivada de 5x es 5.
– La derivada de 2 (una constante) es 0.
Así que, sumando todo, tenemos f'(x) = 6x + 5.
Simplificando la Respuesta
En este caso, nuestra respuesta ya está simplificada. Ahora sabemos que la tasa de cambio de la función 3x^2 + 5x + 2 en cualquier punto x es 6x + 5. ¡Eso es emocionante!
Aplicaciones de las Derivadas
Las derivadas no son solo un concepto teórico; tienen aplicaciones prácticas en diversas disciplinas. Desde la física, donde se utilizan para calcular la velocidad y la aceleración, hasta la economía, donde ayudan a determinar los puntos óptimos de producción y costos. Así que, entender cómo funcionan las derivadas puede abrirte muchas puertas en el mundo académico y profesional.
Ejemplos en el Mundo Real
Imagina que estás diseñando un nuevo producto y quieres maximizar tus ganancias. Usar derivadas puede ayudarte a encontrar el punto en el que tus costos son más bajos y tus ingresos son más altos. ¿No es genial pensar que un concepto matemático puede tener un impacto tan real en tu vida?
¿Por qué la derivada de una constante es cero?
La derivada de una constante es cero porque no hay cambio. Una constante no varía con respecto a la variable, así que su tasa de cambio es nula.
¿Qué otras reglas de derivación debo conocer?
Además de la regla de la potencia, la regla del producto y la regla del cociente, hay reglas como la regla de la cadena, que es muy útil para funciones compuestas.
¿Dónde puedo aplicar el cálculo de derivadas en la vida diaria?
Las derivadas se aplican en muchos campos, incluyendo la física, la economía, la biología y la ingeniería. Desde calcular la velocidad de un coche hasta optimizar costos en una empresa, ¡las posibilidades son infinitas!
¿Cómo puedo practicar más derivadas?
Existen muchos recursos en línea, como ejercicios interactivos, videos y aplicaciones que pueden ayudarte a practicar derivadas. También, no dudes en consultar libros de texto de matemáticas para más ejemplos y ejercicios.
¿Las derivadas son difíciles de entender?
Al principio, pueden parecer complicadas, pero con práctica y comprensión de los conceptos básicos, se vuelven más manejables. ¡La clave es la práctica constante!
¡Y ahí lo tienes! Ahora tienes una comprensión más clara de cómo calcular la derivada de 1 x 2 y cómo aplicar este conocimiento a funciones más complejas. Recuerda, las matemáticas son un viaje, y cada paso que das te acerca más a convertirte en un experto. ¡Sigue practicando y divirtiéndote con el aprendizaje!