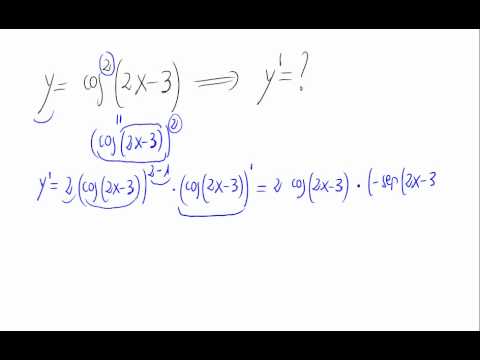¿Alguna vez te has preguntado cómo se comportan las funciones trigonométricas cuando hablamos de derivadas? Si es así, has llegado al lugar correcto. En este artículo, vamos a explorar la derivada del coseno cuadrado, una función que aparece con frecuencia en el análisis matemático y que puede parecer un poco intimidante al principio. Pero no te preocupes, aquí desglosaremos todo el proceso paso a paso, con ejemplos prácticos y explicaciones claras para que puedas comprenderlo sin complicaciones.
El coseno cuadrado, denotado como ( cos^2(x) ), es simplemente el cuadrado de la función coseno. Esto significa que cuando tomamos la derivada de ( cos^2(x) ), no solo estamos trabajando con una función trigonométrica, sino que también estamos aplicando algunas reglas de derivación importantes. Así que, si estás listo, ¡vamos a sumergirnos en el mundo de las derivadas!
¿Qué es la Derivada y por Qué es Importante?
Antes de sumergirnos en la derivada del coseno cuadrado, es crucial entender qué es una derivada. En términos simples, la derivada de una función en un punto nos dice la pendiente de la tangente a la curva de esa función en ese punto. Piensa en ello como la velocidad de un coche: si estás conduciendo y miras el velocímetro, la velocidad que ves es como la derivada; te dice qué tan rápido estás cambiando tu posición en un momento específico.
Las derivadas son fundamentales en cálculo porque nos permiten entender cómo cambian las cosas. Por ejemplo, si estás estudiando cómo varía la altura de un objeto en caída libre, la derivada te dará información sobre su velocidad en cualquier instante. Ahora que hemos establecido la importancia de las derivadas, volvamos al coseno cuadrado.
La Regla de la Cadena: Tu Aliada en el Camino
Cuando hablamos de la derivada del coseno cuadrado, la regla de la cadena es nuestra mejor amiga. Esta regla se utiliza cuando tienes una función compuesta, es decir, una función dentro de otra. En nuestro caso, ( cos^2(x) ) es ( (cos(x))^2 ), lo que significa que estamos lidiando con una función compuesta.
La regla de la cadena establece que si tienes una función ( f(g(x)) ), su derivada se calcula como ( f'(g(x)) cdot g'(x) ). Para el coseno cuadrado, esto se traduce en:
1. Derivada de ( u^2 ) donde ( u = cos(x) ) es ( 2u cdot u’ ).
2. La derivada de ( cos(x) ) es ( -sin(x) ).
Por lo tanto, si aplicamos la regla de la cadena a ( cos^2(x) ), obtenemos:
[ frac{d}{dx}(cos^2(x)) = 2cos(x)(-sin(x)) ]
Lo que simplificamos a:
[ -2cos(x)sin(x) ]
Ejemplo Práctico: Derivando ( cos^2(x) )
Ahora que tenemos la fórmula, vamos a ponerla en práctica con un ejemplo. Supongamos que queremos encontrar la derivada de ( cos^2(2x) ). Primero, aplicamos la regla de la cadena:
1. Identificamos ( u = cos(2x) ).
2. La derivada de ( u^2 ) es ( 2u cdot u’ ).
3. La derivada de ( cos(2x) ) es ( -sin(2x) cdot 2 ) (aplicando la regla de la cadena nuevamente).
Así que ahora, uniendo todo:
[ frac{d}{dx}(cos^2(2x)) = 2cos(2x)(-sin(2x) cdot 2) = -4cos(2x)sin(2x) ]
¡Y ahí lo tienes! La derivada de ( cos^2(2x) ).
Más Ejemplos para Solidificar el Conocimiento
Siempre es útil practicar con más ejemplos para asegurarte de que comprendes el concepto. Vamos a ver otro caso: ( cos^2(3x) ).
1. Aquí, ( u = cos(3x) ).
2. La derivada de ( u^2 ) sigue siendo ( 2u cdot u’ ).
3. La derivada de ( cos(3x) ) es ( -sin(3x) cdot 3 ).
Entonces, aplicamos la regla de la cadena:
[ frac{d}{dx}(cos^2(3x)) = 2cos(3x)(-sin(3x) cdot 3) = -6cos(3x)sin(3x) ]
¿Ves cómo se repite el proceso? Cuanto más practiques, más fácil te resultará.
Aplicaciones de la Derivada del Coseno Cuadrado
Las derivadas del coseno cuadrado tienen aplicaciones en muchos campos, desde la física hasta la ingeniería. Por ejemplo, en la física, se utilizan para analizar movimientos oscilatorios, como el movimiento de un péndulo o las ondas sonoras. Además, en la ingeniería, pueden ser útiles en el diseño de estructuras que deben soportar fuerzas variables.
Imagina que estás diseñando un puente. Necesitas saber cómo las fuerzas cambian a medida que el viento sopla y las cargas cambian. Aquí es donde las derivadas se convierten en herramientas valiosas para calcular la estabilidad y la resistencia del puente. En resumen, entender la derivada del coseno cuadrado no solo es un ejercicio académico, sino que tiene aplicaciones prácticas en el mundo real.
¿Cuál es la derivada de ( cos^2(x) ) en términos de otras funciones trigonométricas?
La derivada de ( cos^2(x) ) se puede expresar como ( -sin(2x) ). Esto se debe a que ( -2cos(x)sin(x) ) es igual a ( -sin(2x) ) utilizando la identidad del ángulo doble.
¿Cómo puedo aplicar la derivada del coseno cuadrado en problemas de optimización?
En problemas de optimización, puedes utilizar la derivada para encontrar máximos y mínimos de funciones que involucren el coseno cuadrado. Al establecer la derivada igual a cero, puedes determinar los puntos críticos y luego evaluar la función en esos puntos.
¿La derivada del coseno cuadrado tiene alguna relación con la integral del seno cuadrado?
Sí, hay una relación. La integral del seno cuadrado es un tema que a menudo se estudia junto con las derivadas de funciones trigonométricas. Ambas funciones están conectadas a través de las identidades trigonométricas y las propiedades de las funciones derivadas e integradas.
¿Es posible derivar ( cos^2(x) ) sin usar la regla de la cadena?
No es recomendable, ya que la regla de la cadena es la forma más eficiente y precisa de derivar funciones compuestas. Sin embargo, siempre puedes expandir ( cos^2(x) ) usando la identidad ( cos^2(x) = frac{1 + cos(2x)}{2} ) y luego derivar.
¿Qué otros temas relacionados debería estudiar para comprender mejor las derivadas de funciones trigonométricas?
Te recomendaría estudiar las identidades trigonométricas, las reglas de derivación (como la regla del producto y la regla del cociente) y la aplicación de las derivadas en la resolución de problemas de optimización y movimiento.
En conclusión, la derivada del coseno cuadrado es un tema fascinante y muy útil en matemáticas. A medida que practiques más, te sentirás más cómodo con las derivadas y su aplicación en diferentes campos. ¡Así que sigue practicando y explorando!